Процедура выявления трендов
При рассмотрении массива данных, сформированного по временному признаку, анализ начинается с рядов динамики. Чтобы получить ряд динамики, по оси Ох отмечаются интервалы времени, в которых были проведены замеры информации. Интервалы должны быть одинаковыми. По оси Оу откладывается значение параметров, после чего полученные точки соединяются ломаными линиями. Ряд динамики подвержен случайным воздействиям, по нему трудно сделать заключение об истинных тенденциях изменения параметров во времени.
Истинное изменение параметра во времени называют трендом. Для выявления тренда можно воспользоваться двумя методами:
1. Метод аналитического выравнивания. Целью аналитического выравнивания динамического ряда является определение аналитической или графической зависимости у(х). На практике по имеющемуся временному ряду задают вид и находят параметры функции, а затем анализируют поведение отклонений от тенденции. Функцию выбирают таким образом, чтобы она давала содержательное объяснение изучаемого процесса.
Аналитическое выравнивание по прямой линии. Линейная зависимость уt = а0 + а1 · t выбирается в тех случаях, когда в исходном временном ряду наблюдается более или менее постоянные абсолютные приросты, не проявляющие тенденции ни к увеличению, ни к снижению. Чтобы воспользоваться аналитическим выравниванием по прямой необходимо: 1) создать ряд динамики; 2) ввести дополнительную условную ось времени.
Если количество наблюдений в ряду динамики четное, то для введения условной оси времени необходимо разделить ряд пополам и с обеих сторон проставить положительные и отрицательные нечетные числа. Если количество наблюдений нечетное, то необходимо выделить центральное значение. Оно будет соответствовать нулевому значению условного времени. От него вверх и вниз будут располагаться положительные и отрицательные целые числа.
Параметры прямой у = а0 + а1 · t находятся с помощью метода наименьших квадратов:
а0 = ∑ уt / n; а1 = ∑ уt t / ∑ t2,
где уt – значение параметра в момент времени t; n – число наблюдений.
На практике с помощью аналитического выравнивания по прямой можно, например, проанализировать качество планирования на предприятии, тенденции изменения по разным составляющим структур (с помощью коэффициентов опережения), показатели, на которые наложен строгий регламент, определить процентное соотношение между средним уровнем и темпом прироста (а0 – средний уровень; а1 – темп прироста) и т. п.
Недостатком прямой линии является то, что здесь не выявляются пики и точки перегиба нелинейных процессов. Для устранения этого недостатка используют, например, параболическую зависимость.
Аналитическое выравнивание по параболе
уt = а0 + а1 · t + а2 · t 2
используется на практике реже. Для расчета параметров параболы решается система уравнений:
 а1 = ∑ уt t / ∑ t2; а0 n + а2 ∑ t2 = ∑ уt,
а1 = ∑ уt t / ∑ t2; а0 n + а2 ∑ t2 = ∑ уt,
а0 ∑ t2 + а2 ∑ t4 = ∑ уt t2.
Если выравнивание по параболе и прямой практически совпадают, то тенденция считается устойчивой.
2. Метод скользящей средней.
Скользящая средняя не имеет аналитического выражения, но сохраняет все точки перегиба, которые являются внутренним неотъемлемым свойством изучаемого процесса и не зависит от субъективных факторов. Они позволяет получать прогноз на уровне 95 % вероятности и выше, поэтому применяется очень широко. В методе скользящих средних исходные уровни ряда заменяются средними величинами, которые получают из данного уровня и нескольких симметрично его окружающих. Целое число уровней, по которым рассчитывается среднее значение, называют интервалом сглаживания.
Усредненные данные для 8 рядов наблюдений за временными процессами, отслеживаемыми в дискретные равностоящие моменты времени (посуточно за месяц) приведены в табл. 1–5 приложения. Для всех 8 рядов определим линейные тренды и проведем аналитическое выравнивание по прямой и параболе. Результаты представлены на рис. 1.1–1.8. Расчетные данные для построения скользящей средней (посуточно) приведены в табл. 6 приложения. При построении скользящей средней длина интервала сглаживания равна 3.
Уравнение прямой (рис. 1.1) имеет вид у1 = 253,68 + 0,36 · t.Анализ графиков позволяет сделать вывод о том, что переработка руды не является стабильным процессом. Имеются значения, которые значительно отличаются от средней величины. Нестабильность подтверждается расхождениями между графиками прямой и параболы, т. е. имеется расхождение между случайными минимальными и максимальными значениями.
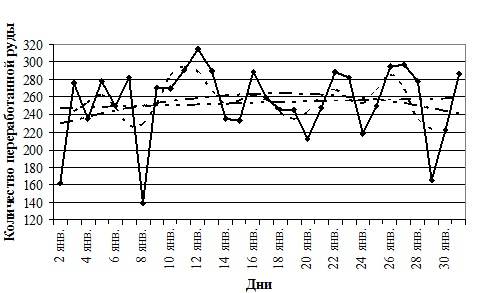
 |
Рис. 1.1. Скользящая средняя и тренд для количества переработанной руды:
Уравнение прямой (рис. 1.2) имеет вид у2 = 0,58 + 0,005 · t. Содержание металла в руде нестабильно, хотя есть участки (т. е. дни) когда значения не значительно отличаются от средней величины. Эта нестабильность подтверждается расхождениями между графиками прямой и параболы, где также можно увидеть совпадение графиков прямой и параболы.
Уравнение прямой (рис. 1.3) имеет вид у3 = 0,65 + 0,01 · t.Выходная концентрация нестабильна. Имеются значения, которые значительно отличаются от средней величины. Но, как и в предыдущем случае, часто значения незначительно отличаются от средней величины. Нестабильность подтверждается расхождениями между графиками прямой и параболы, также наблюдаются совпадения графиков прямой и параболы.
Уравнение прямой (рис. 1.4) имеет вид у4 = 66,5 – 0,05 · t.Содержание металла в концентрате стабильно, поскольку значения незначительно отличаются от средней величины. Эту стабильность подтверждается практическим совпадением прямой и параболы.

 |
Рис. 1.2. Скользящая средняя и тренд для содержания металла в руде:
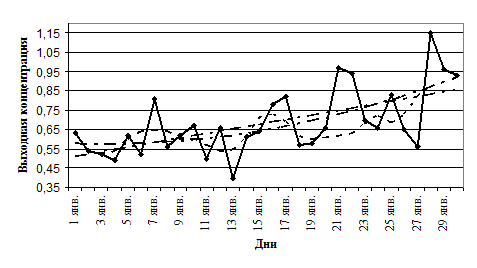
 |
Рис. 1.3. Скользящая средняя и тренд для выхода концентрата:
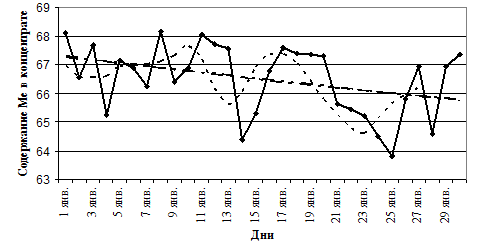
 |
Рис. 1.4. Скользящая средняя и тренд для содержания металла в концентрате:
Уравнение прямой (рис. 1.5) имеет вид у5 = 0,43 – 0,001 · t.Из анализа графиков следует, что содержание серы в концентрате нестабильно. Имеются значения, которые значительно отличаются от средней величины на всем протяжении съема информации. Эта нестабильность также подтверждается расхождениями между графиками прямой и параболы, т. е. есть расхождение между случайными минимальными и максимальными значениями.

 |
Рис. 1.5. Скользящая средняя и тренд для содержания серы в концентрате:
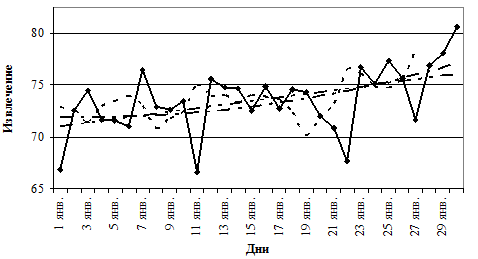
Уравнение прямой (рис. 1.6) имеет вид у6 = 73,56 + 0,17 · t. Извлечение стабильно, поскольку значения незначительно отличаются от средней величины. Эта стабильность заметна из практического совпадения прямой и параболы.
 |
Рис. 1.6. Скользящая средняя и тренд для извлечения:
Уравнение прямой (рис. 1.7) имеет вид у7 = 0,14 + 0,000 5 · t. Содержание металла в хвосте имеет устойчивую тенденцию, поскольку значения незначительно отличаются от средней величины. Эта устойчивость подтверждается практическим совпадением прямой и параболы.

Рис. 1.7. Скользящая средняя и тренд для содержания металла в хвосте:
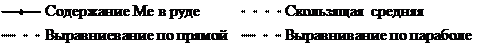
Уравнение прямой (рис. 1.8) имеет вид у8 = 0,6 – 0,01 · t. Анализ графиков показывает, что содержание металла в сульфате нестабильно. Имеются значения, значительно отличающиеся от средней величины. Эта неустойчивость просматривается между графиками прямой и параболы, т. е. есть расхождение между случайными минимальными и максимальными значениями.
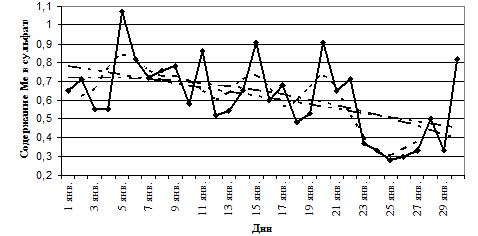
Рис. 1.8. Скользящая средняя и тренд для содержания металла в сульфате:
На основе построенных графиков можно сделать общий вывод о том, что на предприятии имеется много неустойчивых тенденции, что, вероятнее всего, можно объяснить спецификой переработки руды в сложных условиях. При исследовании параметров ряда динамики методом выравнивания скользящей средней можно наблюдать «зоны свободного падения» и «зоны свободного полета» содержания серы в концентрате и металла в концентрате, где содержание нестабильно. Также имеются зоны стабильности («выхода на плато»): в выходной концентрации, содержании металла в концентрате, содержании серы в концентрате, в извлечении, содержании металла в хвосте.
Очевидно, что планирование производства на некоторых участках несовершенно, следовательно, на данном производстве следует пересмотреть систему планирования и нормирования параметров.
Для развернутого анализа подсчитываются коэффициенты опережения, которые показывают различия в темпах, изменения показателя по каждой группе показателей. При этом получены значения:
1) содержание металла в руде и выходная концентрация – 63,69 %;
2) содержание металла в руде и содержание металла в концентрате – 9,74 %;
3) содержание металла в руде и извлечение – 2,89 %;
4) содержание металла в руде и содержание металла в сульфате – 34,47 %;
5) выходная концентрация и содержание металла в концентрате – 15,29 %;
6) выходная концентрация и извлечение – 4,54 %;
7) выходная концентрация и содержание металла в сульфате – 54,12;
8) содержание металла в концентрате и извлечение – 29,66 %;
9) содержание серы в концентрате и извлечение – 0,47 %;
10) содержание серы в концентрате и содержание металла в сульфате – 5,62 %;
11) содержание металла в хвосте и содержание металла в сульфате – 3,56 %.
Полные данные представлены в табл. 7 приложения.
При разбиении ряда динамики на несколько периодов есть возможность выявить для каждого периода свой тренд. Ряды динамики для количества переработанной руды, разбитые по декадам представлены на рис. 1.9–1.11. При построении скользящей средней длина интервала сглаживания равна 3.
Уравнение прямой (рис. 1.9) имеет вид у = 245,53 + 4,3 · t. Количество переработанной руды в 1-й декаде стабильно, поскольку значения незначительно отличаются от средней величины. Эту стабильность подтверждается практическим совпадением прямой и параболы.
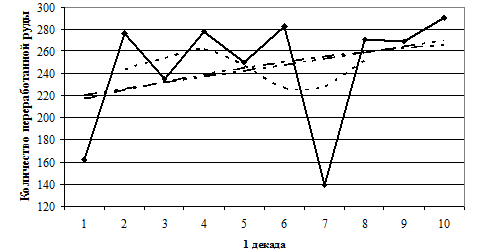
Рис. 1.9. Скользящая средняя и тренд для количества переработанной руды в 1-й декаде:
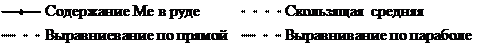
Уравнение прямой (рис. 1.10) имеет вид у = 257,25 – 5,58 · t.Количество переработанной руды во 2-й декаде нестабильно. Имеются значения, которые значительно отличаются от средней величины на всем протяжении съема информации. Эта нестабильность подтверждается расхождениями между графиками прямой и параболы, т. е. есть расхождение между случайными минимальными и максимальными значениями.

Рис. 1.10. Скользящая средняя и тренд для количества переработанной руды во 2-й декаде:
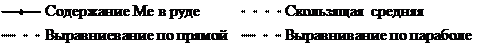
Уравнение прямой (рис. 1.11) имеет вид y = 258,47 + 260,14 · t. Количество переработанной руды в 3 декаде имеет нестабильную тенденцию. Эта нестабильность подтверждается расхождениями между графиками прямой и параболы. Имеются значения, которые значительно отличаются от средней величины. Но, как и в предыдущем случае, иногда значения отличаются незначительно от средней величины.

Рис. 1.11. Скользящая средняя и тренд для количества переработанной руды в 3-й декаде:
Порядок выполнения работы
1. Выбрать вариант задания из числа приведенных в [3].
2. Изучить процедуру выявления трендов, приведенную в лекционном материале, на примере данных табл. 6 приложения.
3. Провести выравнивание по прямой и параболе для своего варианта.
4. Построить скользящую среднюю для своего варианта в соответствии с приведенной методикой.
5. Совместить полученные графики трендов и провести анализ результатов в произвольной форме.
Контрольные вопросы
1. Что такое тренд?
2. Какому закону статистики обычно подчиняются исходные данные для анализа временного ряда?
3. Полином, какой степени чаще всего используется для сглаживания временных рядов?
4. В чем сущность метода скользящего среднего?
5. Какой метод используется для определения параметров прямой, аппроксимирующей временной ряд?
Лабораторная работа 2
Аналитические группировки
Цель работы: познакомиться с типами группировок.
Группировки
После проведения анализа временных трендов можно переходить к анализу распределения результативного признака, который осуществляется с помощью группировок.
Группировкой называется разделение единиц совокупности на группы по существенному варьирующему признаку. Существуют типологическая, аналитическая, структурная и объемная группировки. Отдельно для всех типов группировок существуют вторичные группировки.
На основе типологической группировки дается сравнительная характеристика эффективности различных направлений деятельности. На практике группировки такого вида используются редко из-за неоднозначности их трактовки.
Аналитическая группировка определяет взаимосвязи между различными признаками для единиц одной совокупности.
Структурная группировка характеризует распределение единиц однотипной совокупности по признакам. Ее можно проводить в зависимости от выбранных признаков: а) атрибутивных; б) количественных (интервальных).
На производстве распространение получил количественный признак. Для проведения интервальной группировки задается интервал. Для определения влияния того или иного фактора или комбинации факторов, на рассматриваемый результативный признак проводятся объемные группировки.
Для проведения аналитической группировки назначается группировочный признак. В качестве показателя принимается изучаемый признак, который фиксируется на двух уровнях – абсолютном и относительном.
Если в аналитической группировке скачки между уровнями составляют более 5 %, то влияние группировочного признака предполагается существенным. Для проверки этого предположения необходимо провести однофакторный дисперсионный анализ.
Проведем анализ, используя приведенные усредненные данные по дням недели (табл. 3 приложения), по сменам (табл. 4 приложения), по категориям мастера (табл. 5 приложения). В качестве целевых признаков берутся все параметры.
