Оптимизация структуры электрической сети

Итерационные методы расчетов установившихся режимов электрических систем

Требуется составить систему уравнений контурных токов 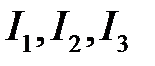и решить ее методами.

1)Методом простых итераций

2)Зейделя

3)Гаусса

4)Методом обратной матрицы

5)Гаусса – Жордана

Параметры:

R1=20 Ом

R2=15 Ом

R3=10 Ом

R4=900 Ом

R5=1100 Ом

U1=120 кВ

U2=115 кВ

Требуемая точность

Решение:

1) Метод простых итераций:

Составим систему уравнений контурных токов :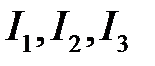

Запишем систему в нормальном виде:

Найдем свободные члены:

Метод простых итераций:

Выберем нулевое приближение:

A

A

Найдем первые приближения:

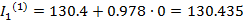A

A

Проверка:

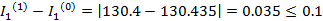
Проверка не сошлась.

Найдем вторые приближения:

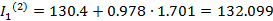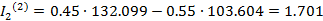A

A

Проверка:

Проверка не сошлась.

Найдем третьи приближения:

A

A

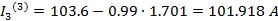
Проверка:

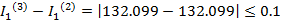
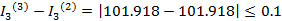
Проверка не сошлась.

Найдем четвертые приближения:

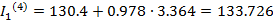A

A

Проверка:

Проверка не сошлась.

Найдем погрешность расчета:

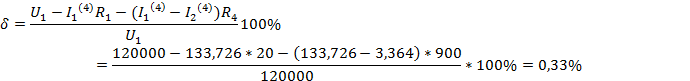
Метод Зейделя

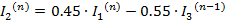
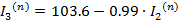
Выберем нулевое приближение:

A

A

Найдем первые приближения:

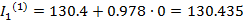A

A

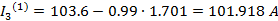
Проверка:

Проверка не сошлась.

Найдем вторые приближения:

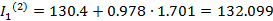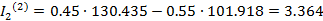A

A

Проверка:

Проверка не сошлась.

Найдем третьи приближения:

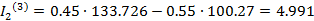A

A

Проверка:

Проверка не сошлась.

Найдем четвертые приближения:

A

A

Проверка:

Проверка не сошлась.

Найдем погрешность расчета:

Метод Гаусса

Составим систему уравнений;

Выполним прямой ход:

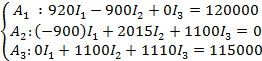
Коэффициент исключения:

Умножим первое уравнение А1 поочередно на коэффициент исключения и сложим с А2 и А.

Получим промежуточную систему уравнений:

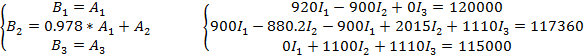
После расчёта:

Умножим первое уравнение промежуточной системы B2 на коэффициент исключения:

И сложим первое уравнение со вторым промежуточной системы, т.е. B3:

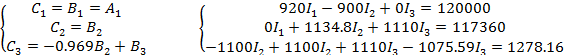
После расчёта:

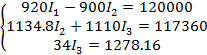
Выполним обратный ход.

Подставим I3 во второе уравнение. Найдем I2. Подставим I2 и I3 в первое уравнение и найдем I1:

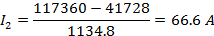
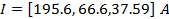
4) Метод Гаусса – Жордана

Исходные уравнения:

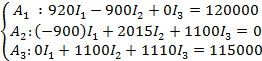
Ведущая строка – первая. Относительно неё ведем преобразования.

Вычисляем:

Далее ведущая строка – вторая:

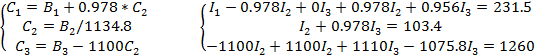
После расчетов:

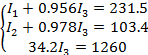
Далее работаем с третьей строкой:

Таким образом, мы получили решение системы уравнений без обратного хода.

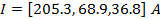
Метод обратной матрицы

Запишем уравнение контурных токов в матричном виде:

умножим слева на

можно записать:

где

Запишем исходную матрицу:

Найдем ее определитель:

Найдем алгебраические дополнения:

Проверка:

Т.к получили единичную матрицу, то матрицу собственных и взаимных проводимостей нашли верно. Теперь найдем вектор контурных токов.

Сводная таблица:

Название метода	I1 , А	I2 , А	I3 , А
Метод простой итерации	133,726	3,364	100,27
Метод Зейделя	135,317	6,582	97,081
Метод Гаусса		66,6	37,59
Метод Гаусса-Жордана		68,9	36,8
Метод обратной матрицы	205,821	77,062	27,236

Методы оптимизации потокораспределения мощности в электрической сети.

Дано:

т .р у б /к м

т .р у б /к м

Симплекс метод

Построим математическую модель задачи, учитывая, что пропускная способность отходящих ЛЭП не должна превышать установленной мощности источника, а пропускная способность линий питающих узел нагрузки должна быть равна его потреблению.

Для применения симплекс метода задачу необходимо привести к канонической форме, т.е. перейти к строгим равенствам в ограничениях.

Для этого введем вспомогательные переменные Х₅ и Х₆:

Первый шаг:

Выбираем в качестве базисных переменных Х₂, Х₃, Х₅, Х₆, а в качестве свободных Х₁, Х₄. Выразим в ограничениях базисные переменные через свободные.

Пусть все свободные члены будут равны нулю, тогда значения базисных переменных:

В результате получаем базисное решение (0,40,45,0,10,-5) соответствующее базису Б1(Х₂,Х₃,Х₅,Х₆). Значение целевой функции, соответствующее базисному решению первого шага:

Коэффициент при Х4 отрицателен, следовательно, возрастание Х4 приведет к дальнейшему уменьшению целевой функции. Однако возрастание Х4 будет уменьшать Х2 и Х6 и необходимо следить затем, чтобы они не стали отрицательными.

Второй шаг:

Выбираем в качестве базисных переменных Х₂, Х₃, Х₅, Х₄, а в качестве свободных Х₁, Х₆. Выразим в ограничениях базисные переменные через свободные.

В результате получаем базисное решение (0,54,45,-14,-4,0) соответствующее базису Б2(Х₂,Х₃,Х₄,Х₅). Значение целевой функции, соответствующее базисному решению первого шага:

При X₁ стоит -4.5, и следовательно мы не достигли наименьшего значения.

Выберем другую свободную переменную вместо X₁.

Третий шаг:

Выбираем в качестве базисных переменных Х₁, Х₂, Х₄, Х₅, а в качестве свободных Х₃, Х₆. Выразим в ограничениях базисные переменные через свободные.

В результате получаем базисное решение (45,0,0,40,5,0) соответствующее базису Б3(Х₁,Х₂,Х₄,Х₅). Значение целевой функции, соответствующее базисному решению первого шага:

Новое базисное решение (45,0,0,40,5,0)

H1

U2

U1

Это решение является оптимальным.

H2

х5=5

х6=0

Оптимизация структуры электрической сети

Дано:

P₁=35 МВт

P₂=40 МВт

P₃=15 МВт

P₄=25 МВт

P₅=50 МВт

L₀₁=32 км

L₀₂=32 км

L₀₃=32 км

L₀₄=32 км

L₀₅=32 км

L₁₂=32 км

L₁₃=32 км

L₃₅=32 км

L₄₅=32 км

Затраты: З=1,01+0,01P_s

Вводим обозначения:

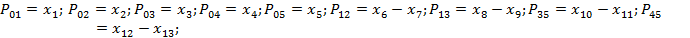
С учетом этого:

K=271.69 свободный член, то есть некоторая постоянная

Модель примет форму:

Определим обратную матрицу:

найдем х:

таким образом:

оптимальность:

Вектор управления не является оптимальным, так как среди оценок имеются отрицательные. Введем в базис вектор А₅, поскольку . Это число занимает четвертую позицию в векторе оценок, а четвертая позиция среди внебазисных переменных соответствует А₅. С целью определения вектора условий, подлежащего удалению из базиса, вычислим компоненты:

и найдем:

Отсюда следует, что надо вывести из базисного вектор условий A₁₀;

Таким образом, на второй итерации:

Сформируем матрицы А_х, С_х, :

Обратная матрица:

Определим базисные компоненты нового опорного плана:

Очередной опорный план:

Проверим его оптимальность:

Вектор управления не является оптимальным, так как среди оценок имеются отрицательные. Введем в базис вектор А₁₁, поскольку . Это число занимает седьмую позицию в векторе оценок, а седьмая позиция среди внебазисных переменных соответствует А₁₁. С целью определения вектора условий, подлежащего удалению из базиса, вычислим компоненты:

и найдем:

таким образом, на третьей итерации:

Сформируем матрицы А_х, С_х, :

Обратная матрица:

Определим базисные компоненты нового опорного плана:

Очередной опорный план:

Проверим его оптимальность:

План Х² оптимален, так как среди оценок нет отрицательных.

Таким образом

С целью проверки и интерпретации полученных результатов :

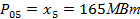
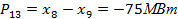
Отрицательные результаты означают, что в оптимальном графе сети нужно сменить на противоположные в сравнении с исходным максимальным графом направления потоков мощности в дугах 13, 35, 45, а дуги 01, 02, 03, 04 вообще исключить из рассмотрения, поскольку там протекают «нулевые» потоки.

Окончательно оптимальный граф:

Рассмотрим как изменились по итерациям приведенные затраты, представляющие собой критерий исследуемой операции. Для этого векторы управления подставим в целевую функцию модели или соответствующие им мощности. Отсюда:

После каждой итерации критериальная функция улучшалась. Учитывая строгое соответствие каждого опорного плана системе ограничений, можно говорить о действительной оптимизации конфигурации сети.