Підмножина. рівність множин.
Означення 2.5. Множина  називається підмножиною множини
називається підмножиною множини  , якщо кожен елемент
, якщо кожен елемент  є елементом
є елементом  .
.
Для позначення цього факту вводиться знак «  » – символ включення (або «
» – символ включення (або «  »); іншими словами,
»); іншими словами, 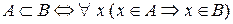 .
.
Якщо необхідно підкреслити, що множина  містить також інші елементи, крім елементів множини В, то використовують символ строгого включення:
містить також інші елементи, крім елементів множини В, то використовують символ строгого включення: 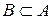 . Зв’язок між символами
. Зв’язок між символами  і
і  задається виразом
задається виразом  . Загалом будемо використовувати символ «
. Загалом будемо використовувати символ «  ».
».
Говорять, що множина  є істинною (або власною, від слова «власне») підмножиною
є істинною (або власною, від слова «власне») підмножиною  , якщо
, якщо 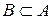 і
і  на відміну від неістинних (або невласних) підмножин Æ та
на відміну від неістинних (або невласних) підмножин Æ та  будь-якої множини
будь-якої множини  .
.
Приклад 2.8. Стосовно вищенаведеного приклада підмножинами множини U співробітників деякої фірми є множини  ,
,  ,
, 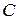 ,
, 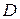 ,
,  ,
,  ,
, 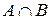 ,
, 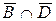 ,
, 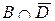 . Крім того можна розглядати, що
. Крім того можна розглядати, що
 – множина співробітників фірми, яким за віком більш 40 років, є підмножиною множини співробітників за віком більш 30 років.
– множина співробітників фірми, яким за віком більш 40 років, є підмножиною множини співробітників за віком більш 30 років.
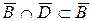 ,
,  – множина співробітників фірми за віком не більш 30 років, які мають стаж роботи не більш 5 років, є підмножиною множини співробітників фірми, яким за віком не більш 30, й одночасно є підмножиною множини співробітників фірми, які мають стаж роботи не більш 5 років.
– множина співробітників фірми за віком не більш 30 років, які мають стаж роботи не більш 5 років, є підмножиною множини співробітників фірми, яким за віком не більш 30, й одночасно є підмножиною множини співробітників фірми, які мають стаж роботи не більш 5 років.
Підкреслимо, що всі наведені приклади підмножин є прикладами істинних підмножин.
Порожня множина не містить елементів. Отже, додаючи до множини  порожню множину, ми фактично нічого не додаємо. Тому завжди можна вважати, що будь-яка множина
порожню множину, ми фактично нічого не додаємо. Тому завжди можна вважати, що будь-яка множина  містить порожню множину як підмножину.
містить порожню множину як підмножину.
Приклад 2.9.Нехай 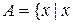 – людська істота} і
– людська істота} і 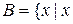 – людська істота жіночої статі}; тоді зрозуміло, що
– людська істота жіночої статі}; тоді зрозуміло, що 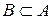 , а
, а  – істинна підмножина
– істинна підмножина  .
.
Треба бути уважним, щоб розрізняти елементи множини та підмножини цієї множини. Наприклад, коли пишуть 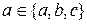 це означає, що елемент
це означає, що елемент 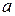 є членом множини, що складається з трьох елементів:
є членом множини, що складається з трьох елементів: 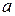 ,
, 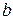 і
і  . Коли ж пишуть
. Коли ж пишуть 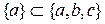 , це означає, що множина, що складається з одного елемента
, це означає, що множина, що складається з одного елемента 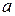 , є підмножиною множини, яка складається з трьох елементів:
, є підмножиною множини, яка складається з трьох елементів: 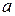 ,
, 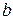 ,
,  .
.
Таким чином, якщо Розов А.Ю. є студентом групи 1ЕК, то це означає, що цей студент є елементом множини  студентів групи 1ЕК. Якщо це єдиний студент цієї групи, який склав зимову сесію на “відмінно”, то студент Розов А.Ю., є єдиним елементом множини
студентів групи 1ЕК. Якщо це єдиний студент цієї групи, який склав зимову сесію на “відмінно”, то студент Розов А.Ю., є єдиним елементом множини  студентів-відмінників групи 1ЕК за результатами зимової сесії, при чому
студентів-відмінників групи 1ЕК за результатами зимової сесії, при чому 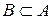 .
.
Означення 2.6. Дві множини рівні, якщо вони складаються з одних і тих самих елементів:
 .
.
Наприклад, 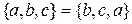 .
.
Справджується таке твердження:
Тоді і тільки тоді, коли .
Можна довести таке твердження: включення множин транзитивне, тобто справджується така рівність:
якщо  , то
, то 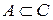 .
.
Множина підмножин
Слід розуміти, що елементи множини самі можуть бути деякими множинами. Наприклад, книга з множини книг у шафі може розглядатися як множина сторінок. Потрібно звернути увагу на те, що йдеться про елементи множини, а не про підмножини (ніяка сукупність сторінок не може розглядатися як підмножина множини книг).
Множина  груп факультету складається із груп, тобто елементом множини
груп факультету складається із груп, тобто елементом множини  є група, як неподільне ціле, в той самий час кожна група є множиною студентів, але окремий студент не є елементом множини
є група, як неподільне ціле, в той самий час кожна група є множиною студентів, але окремий студент не є елементом множини  груп факультету.
груп факультету.
Означення 2.7. Множину, елементами якої є всі підмножини множини  , називають множиною підмножин (множиною-степенем) множини
, називають множиною підмножин (множиною-степенем) множини  і позначають
і позначають 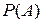 .
.
Приклад 2.10.Для триелементної множини 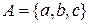 маємо
маємо
 .
.
У разі кінцевої множини  , що складається з n елементів, множина підмножин
, що складається з n елементів, множина підмножин 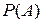 містить
містить  елементів. Слід підкреслити відмінності між відношенням належності (
елементів. Слід підкреслити відмінності між відношенням належності ( 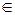 ) і відношенням включення (
) і відношенням включення (  ). Як уже зазначалося, множина
). Як уже зазначалося, множина  може бути своєю підмножиною (
може бути своєю підмножиною ( 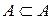 ), але вона не може входити до складу своїх елементів (
), але вона не може входити до складу своїх елементів ( 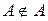 ). Навіть у разі одноелементних підмножин потрібно відрізняти множину
). Навіть у разі одноелементних підмножин потрібно відрізняти множину  та її єдиний елемент а (дивись приклад). Відношення включення має властивість транзитивності, відношення належності цієї властивості не має. Тобто, із того, що
та її єдиний елемент а (дивись приклад). Відношення включення має властивість транзитивності, відношення належності цієї властивості не має. Тобто, із того, що  не витікає, що
не витікає, що 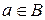 , як здається на перший погляд.
, як здається на перший погляд.
Приклад 2.11. Розглянемо такі множини  ,
, 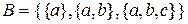 . Дійсно
. Дійсно 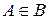 , але
, але  .
.
Алгебра множин
Закони алгебри множин
Операції над множинами, як і операції над логічними змінними, мають деякі властивості. Останні виражаються сукупністю тотожностей незалежно від конкретного вмісту множин, що входять у них, і є підмножинами деякого універсуму 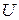 . Ми вже знаємо, що множина об’єктів разом з операціями утворюють алгебру. Множина всіх множин разом з операціями об’єднання, перерізу і абсолютного доповнення утворюють алгебру, яка називається алгеброю множин. Її основні властивості або закони алгебри множин наведені нижче.
. Ми вже знаємо, що множина об’єктів разом з операціями утворюють алгебру. Множина всіх множин разом з операціями об’єднання, перерізу і абсолютного доповнення утворюють алгебру, яка називається алгеброю множин. Її основні властивості або закони алгебри множин наведені нижче.
Комутативні закони
а) 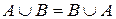 ; ; | б) 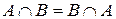 . . |
Асоціативні закони
а) 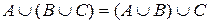 ; ; | б) 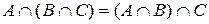 . . |
Дистрибутивні закони
а) 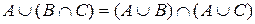 ; ; | б)  . . |
Властивості Æ та 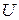
4 а)  ; ; | 4 б) 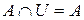 . . |
5 а)  ; ; | 5 б) 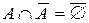 . . |
6 а)  ; ; | 6 б)  . . |
7 а)  ; ; | 7 б) 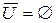 . . |
Закон ідемпотентності (самопоглинання)
8 а) 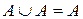 ; ; | 8 б) 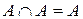 . . |
Закон поглинання
9 а)  ; ; | 9 б) 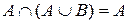 . . |
Теорема де Моргана
