Тема 7. Криптосистеми з відкритим ключем

40. Задачі криптології, які привели до створення асиметричних шифрів.

При практичному застосуванні моделі Шеннона необхідність реалізації захищеного каналу для ключового обміну породжує так називану проблему безпечного поширення ключів.

Крім того, при використанні засобів шифрування в автоматизованих системах, виникає проблема підтвердження істинності події або інформації, зокрема, так званого підпису електронних повідомлень.

Обидві ці задачі, без використання захищеного каналу зв'язку, удалося вирішити в рамках моделі криптосистему з «відкритим» ключем, запропонованої В.Диффи і М.Хеллманом у 1976 році.

Відмінність моделі системи секретного зв'язку В.Диффи і М.Хеллмана від моделі К.Шеннона в тім, що вона є асиметричною у тому сенсі, що користувачі стосовно секретного параметра нерівноправні. Повністю ключ відомий тільки одержувачу повідомлення і являє собою пару 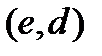де подключ 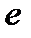(т.зв. відкритий ключ) служить ключем зашифрування, а подключ 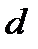служить для расшифрования, при цьому тільки 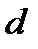є секретним параметром (т.зв. секретний, особистий, приватний ключ).

Ключ відомий тільки одержувачу повідомлень, які відправники повинні шифрувати, використовуючи ключ .

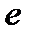Такі криптосистемы називаються асиметричними або системами з відкритими ключами.

41. Поняття про однонапрямлені функції і функції з лазівками.

Стійкість асиметричної криптосистеми забезпечується за рахунок особливих властивостей шифрперетворення, що являє собою так звану однобічну (односпрямовану, важкооборотну) функцію з «лазівкою». Обчислення значення такої функції (від відкритого тексту і параметра ) повинне бути нескладним. У той же час, її обернення повинно бути обчислювально неможливим без знання секретної інформації, «лазівки», пов'язаної з секретним ключем .

Строго кажучи, не доведено, що однобічні функції існують. Однак визнано, що деякі перетворення мають властивості, близьки до властивостей однобічних функцій.

Функція 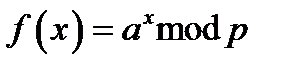, при великих значеннях 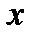і 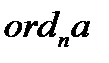, поводиться як однобічна. Реалізовати зворотню функцію (дискретний логарифм) обчислювально неможливо. Аналогічні властивості має степенева функція виду , де .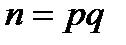

Для обернення цієї функції досить розв’язати задачу факторизації - розкладання числа 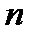на співмножники. Задача факторизації натурального числа і задача дискретного логарифмування є алгоритмічними проблемами теорії чисел.

Абонент, що бажає передати ключ для симетричної криптосистеми, перешифровує його ключем 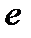одержувача (вважається, що асиметрична система створена заздалегідь і відкритий ключ опублікований). Однобічна функція гарантує безпеку, тому що розшифрувати повідомлення можна тільки знаючи ключ 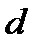, а його знає лише потрібний абонент. Загальновідомо, що даний механізм проте не є безпечним. На практиці виявилося необхідним вводити в глобальному масштабі систему т.зв. центрів сертифікації відкритих ключів. Центр сертифікації відіграє роль довіреної особи, яка підтверджує, що повідомлення, зашифроване даним відкритим ключем, зможе розшифрувати саме той абонент, для якого це повідомлення призначалося.

42. Принципи побудови асиметричної криптосистеми.

Нехай абонент 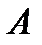вимагає зашифрованих повідомлень від абонента 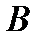. Тоді:

1. Абонент 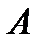вибирає однонапрямлену функцію з лазівкою 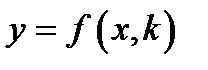публікує алгоритм обчислення значень цієї функції, але значення ключа залишає таємним.

2. За опублікованим алгоритмом абонент обчислює для свого повідомлення значення однонапрямленої функції з лазівкою 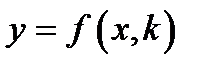і посилає його абоненту по відкритому незахищеному каналу зв'язку.

Тільки абонент 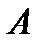, володіючи секретним ключем 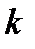, може за відомим значенням функції 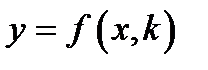визначити аргумент і дешифрувати криптограму.

Щоб гарантувати надійний захист інформації, до систем з відкритим ключем пред'являються дві природні вимоги:

1. Перетворення початкового тексту повинне виключати його відновлення на основі відкритого ключа.

2. Визначення закритого ключа на основі відкритого також повинне бути таким, що обчислювально не реалізовується. При цьому бажано знати точну нижню оцінку складності (кількості операцій) розкриття шифру.

Однонапрямлена функція гарантує безпеку, оскільки розшифрувати повідомлення можна тільки знаючи секретний ключ 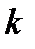, а його знає лише потрібний абонент.

Загальновідомо, що даний механізм все одно не є безпечним. Справа ускладнюється настільки, що на практиці виявилося необхідним вводити в глобальному масштабі систему так званих центрів сертифікації відкритих ключів. Центр сертифікації відіграє роль довіреної особи, яка гарантує, що повідомлення, зашифроване даним відкритим ключем, зможе розшифрувати тільки абонент, для якого це повідомлення призначалося.

43. Затосування криптографії з відкритим ключем. Протокол обміну ключами Діффі–Хеллмана.

При подальшому розвитку, ідея використання однобічних функцій у криптографії дозволила вирішити ряд проблем, пов'язаних із захистом інформації. Так, наприклад, велике число важливих задач вирішується за допомогою інтерактивних процедур, що називаються криптографічними протоколами.

Забезпечення цілісності даних. Цілісність даних - властивість даних, що дозволяє після передачі одержати них в істинному виді, незважаючи на зміни, передбачені протоколом.

Аутентифікація абонента: перевірка того, що абонент дійсно є особою, за яку себе видає.

Аутентифікація повідомлення: перевірка того, що повідомлення передано без змін від заявленого відправника до відповідного кореспондента.

Реальні криптопротоколи відрізняються великою різноманітністю, причому в них використовуються як асиметричні так і симетричні криптоалгоритми.

Для обґрунтування надійності протоколів недостатньо гарантій стійкості застосовуваних криптоперетворень, оскільки обмін інформацією, що підлягає захисту може здійснюватися в умовах взаємної недовіри користувачів.

В даний час у системах зв'язку загального призначення широко поширені т.зв. змішані криптосистеми. У таких системах конфіденційність повідомлень забезпечується за рахунок шифрування за допомогою симетричної криптосистеми, розсилка ключів для якої здійснюється з використанням асиметричних криптоалгоритмов.

Існують стандартизовані протоколи безпечного ключового обміну, що забезпечують у різних ситуаціях побудову загального симетричного ключа.

Найбільш ранній протокол обміну ключами при взаємній недовірі учасників обміну запропонований Діффі і Хеллманом.

Нехай абонент А є ініціатором обміну. Він має намір узгодити спільний секретний ключ для симетричної криптосистемы з абонентом В. Кожному абоненту відоме просте число 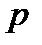і первісний елемент поля .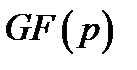

Протокол вирішує проблєму побудови спільного секретного блоку даних виду для подальшої генерації ключів, де - випадкові лишки за модулем .

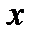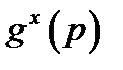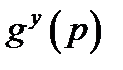Абонент А випадково вибирає число , обчислює значення і відправляє це значення абоненту В. Абонент А діє аналогічно: вибирає , обчислює значення і відправляє це значення абоненту А. Кожний з абонентів тепер у стані обчислити значення загального секретного блоку 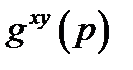. Одержати це значення, виходячи з перехоплення неможливо, внаслідок властивостей дискретного логарифма, а підходів, нееквівалентних дискретному логарифмуванню, не знайдено.

44. Загальні принципи побудови систем управління колючами.

Множина ключових елементів, порядок їх використання і закон формування ключів з ключових елементів складають ключову систему шифру.

В потокових шифрах в даний час поширені трьох- і дворівневі ключові системи. Для трирівневої системи є три види ключів: мережевий, довготривалий і сеансовий. Для дворівневої є два види ключів – довготривалий і сеансовий, мережевий ключ відсутній.

Мережевий ключ є ключовим елементом, термін дії якого може бути необмеженим. Він заноситься при виготовленні конкретної партії пристроїв для мережі зв'язку.

Довготривалий ключ– це ключ, що діє протягом тривалого проміжку часу і змінюється, як правило, періодично.

Сеансовий ключдіє значно коротший інтервал часу, чим базовий. Звичайно один сеансовий ключ використовується на один сеанс зв'язку, тобто на групу повідомлень.

Якщо свій сеансовий ключ виробляється на кожне повідомлення, то він називається разовим ключем.

В даний час, найчастіше, сеансові і разові ключі співпадають. Сумарна довжина ключових елементів в потокових шифрах складає порядку 128-512 і більше бітів.

У мішаних криптосистемах, заснованих на потокових шифрах, розподіл ключів спрощується, оскільки канал доставки сеансових ключів захищений асиметричною криптосистемою, а для таких криптосистем розподіляються тільки відкриті ключі.

Проте замість питання конфіденційності ключа в даному випадку виникає питання його аутентичності, тобто доказу того, що даний відкритий ключ дійсно належить особі, якій призначена криптограма.

Якщо це не так, то конфіденційна інформація буде відправлена не за призначенням.

Для рішення цієї задачі використовується поняття сертифікату відкритого ключа. Сертифікат відкритого ключа (краще сказати, сертифікат власника відкритого ключа) в даному випадку є електронним документом, де розміщується інформація, що підтверджує належність відкритого ключа конкретній особі.

Аутентичність інформації гарантується органом (центром сертифікації), який випустив (створив) сертифікат. Вважається, що учасники обміну повністю довіряють цьому органу.

При використанні сертифікатів, перед кожним застосуванням відкритого ключа відправник змушений звертатися по мережі до електронних засобів, обслуговуючих пошук і доставку відповідних даних.

45. Криптосистема Ель-Гамаля.

Криптосистема Ель-Гамаля є асиметричною. Для побудови пари ключів вибирається велике просте число 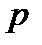і два псевдовипадкові числа, менших 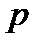. Одне з них, , повинно бути елементом великого порядку за модулем , скажемо, первісним коренем. Друге число, , вибирається як секретний ключ. Припускається, що повідомлення – лишки за модулем .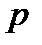

Відкритим ключем є трійка чисел .

Дискретна експонента поводиться як однобічна функція, але не як однобічна функція з лазівкою.

Тому для кожного повідомлення формуються додаткові дані, що грають роль лазівки для конкретного сеансу шифрування.

Для зашифрування повідомлення 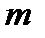вибирається псевдовипадкове число (рандомізатор, разовий ключ) з умовою 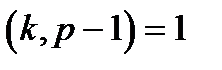. Рандомізатори не повинні повторюватися і повинні утримуватися в секреті.

Потім обчислюються числа 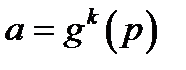- лазівка і 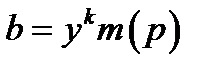- шифротекст. Криптограмою є пара блоків даних: .

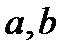Для розшифрування досить одержати співмножник 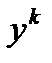, що можна зробити за допомогою секретного ключа, обчисливши значення .

46. Криптосистема RSA.

Широко відома криптографічна система RSA, що запропонована в 1978 році, є асиметричної криптосистемой, основаної на однобічній функції з лазівкою, в якості якої обрана степенева функція у кільці лишків цілих чисел по складеному (біпростому) модулю 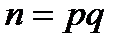. Стійкість системи основана на складності задачі факторизации великих біпростих чисел.

Криптосистема RSA на кожному такті шифрування перетворює двійковий блок відкритого тексту 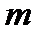довжини 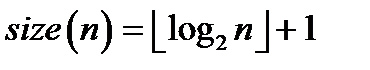, що розглядається як ціле число, за допомогою піднесення до степеню за модулем : 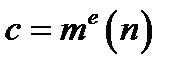. Показник степеня і модуль є елементами відкритого ключа.

Лазівка забезпечується за рахунок секретного ключа 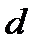, побудованого таким чином, що для усіх 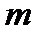виконується співвідношення .

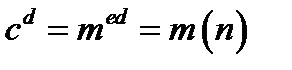Побудова криптосистемы забезпечує одержувач повідомлень.

Спочатку випадковим образом вибираються два різних великих простих числа 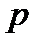і . Обрані прості числа повинні задовільняти деяки додаткові умови. Потім обчислюється модуль 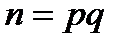, функція Эйлера від модуля , а також вибирається випадкове число , взаємно просте з .

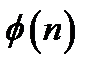Секретний ключ будується за допомогою розширеного алгоритму Евкліда, як число 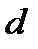, що задовольняє порівнянню . Після цього всі дані, крім 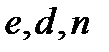, включаючи дані проміжних обчислень, знищуються. Пара 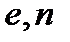опубліковується як відкритий ключ.

Розшифрування забезпечується тим, що для 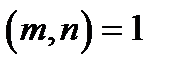з теореми Ейлера випливає 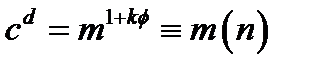і, крім того, для інших значень 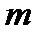співвідношення 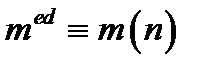також має місце, внаслідок властивостей модуля виду .

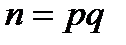47. Криптосистеми на основі еліптичних кривих.

Тема 8. Тестування чисел на простоту.

48. Тестування на простоту та факторизація чисел.

Відрізнити просте число від складеного, а також розкласти останнє на прості множники (факторизувати) є однією з найважливіших задач арифметики. Пошук великих простих чисел необхідний, наприклад, для забезпечення надійності систем шифрування інформації з відкритим ключем. Перевірка на простоту є першим етапом факторизації.

49. Детерміновані тести: метод пробних ділень, решето Ератосфена.

Тест на простоту називається детермінованим, якщо в результаті його застосування можна однозначно встановити, чи є задане число простим чи ні.

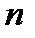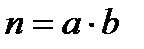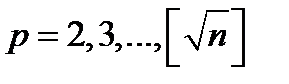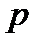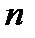Метод пробних ділень.Якщо -складене, то , де , причому . Тому для простих треба перевірити, чи ділиться на . Якщо дільник числа не буде знайдений, то -просте. В противному випадку буде знайдений мінімальний простий дільник числа 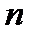, тобто буде отриманий розклад 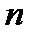на два множники.

Решето Ератосфена дає простий спосіб складання таблиці простих чисел, що не перевищують даного натурального числа .

Спосіб решета Ератосфена полягає у наступному. Виписуємо підряд числа натурального ряду від 1 до :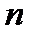

1, 2, 3, 4, 5, 6, 7, 8, 9, 10,…, 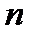(А)

Число 2 є першим в ряду (А), більшим за 1. Викреслимо в ряду (А) всі числа, кратні 2, крім самого 2. Тоді першим невикресленим числом після 2 буде 3. Викреслимо в ряду (А) всі числа, кратні 3, крім самого 3. Тоді першим невикресленим числом після 3 буде 5. Викреслимо в ряду (А) всі числа, кратні 5, крім самого 5, і т.д. Якщо вже викреслені всі числа, що діляться на прості, які не перебільшують 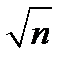, то, за сформульованим правилом, всі числа, що залишилися невикресленими, є простими. Таблицю простих чисел, які не перебільшують числа складено.

50. Тест Ферма. Числа Кармайкла.

Теорема (мала теорема Ферма). Якщо – просте, то для довільного цілого 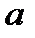, , 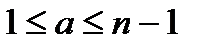має місце конгруенція 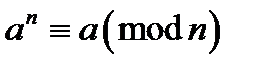, якщо при цьому , то .

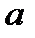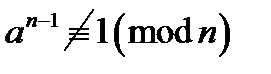Теорема (тест на розкладність). Якщо – непарне натуральне число і знайдеться таке ціле число , , що , то 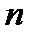– складене.