Тема 2: Отбор факторов, включаемых в модель множественной регрессии
Тема 1: Спецификация эконометрической модели
1. Ошибки спецификации эконометрической модели имеют место вследствие …
неправильного выбора математической функции или недоучета в уравнении регрессии какого-то существенного фактора
недостоверности или недостаточности исходной информации
неоднородности данных в исходной статистической совокупности
недостаточного количества данных
Решение:
Спецификацией модели называется отбор факторов, включаемых в модель, и выбор математической функции для 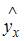 . Поэтому к ошибкам спецификации относятся не только неправильный выбор той или иной математической функции для
. Поэтому к ошибкам спецификации относятся не только неправильный выбор той или иной математической функции для 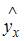 , но и недоучет в уравнении регрессии какого-то существенного фактора, то есть использование парной регрессии вместо множественной.
, но и недоучет в уравнении регрессии какого-то существенного фактора, то есть использование парной регрессии вместо множественной.
2. Для регрессионной модели вида 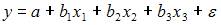 необходим минимальный объем наблюдений, содержащий _____ объектов наблюдения.
необходим минимальный объем наблюдений, содержащий _____ объектов наблюдения.
Решение:
Считается, на каждый оцениваемый коэффициент регрессии необходимо не менее 5–7 объектов статистических наблюдений. Так как представленная модель содержит 3 независимые переменные, то на каждый из параметров регрессии при независимой переменной необходимо по 5–7 наблюдений, то есть в совокупности не менее 15–21 наблюдения. Берем нижнюю границу интервала, тогда правильный вариант ответа – «15».
3. Нелинейным по объясняющим переменным, но линейным по параметрам уравнением регрессии является …
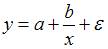
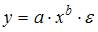
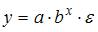
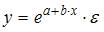
Решение:
Из приведенных функций только в функции 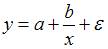 параметры имеют степень 1, а объясняющая переменная х имеет степень, отличную от 1.
параметры имеют степень 1, а объясняющая переменная х имеет степень, отличную от 1.
4. В модели вида 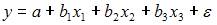 количество объясняющих переменных равно …
количество объясняющих переменных равно …
Решение:
Эконометрическая модель уравнения регрессии может быть представлена линейным уравнением множественной регрессии в виде выражения 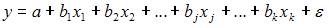 , где y – зависимая переменная; xj – объясняющая независимая переменная (j = 1,…, k; k – количество независимых переменных); a, bj – параметры (a – свободный член уравнения, bj – коэффициент регрессии);
, где y – зависимая переменная; xj – объясняющая независимая переменная (j = 1,…, k; k – количество независимых переменных); a, bj – параметры (a – свободный член уравнения, bj – коэффициент регрессии); 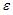 – случайные факторы. Независимые переменные xj называются также факторами, объясняющими переменными. На количество объясняющих переменных в линейном уравнении указывает также количество коэффициентов регрессии bj. Поэтому количество объясняющих переменных в модели равно 3.
– случайные факторы. Независимые переменные xj называются также факторами, объясняющими переменными. На количество объясняющих переменных в линейном уравнении указывает также количество коэффициентов регрессии bj. Поэтому количество объясняющих переменных в модели равно 3.
5. При идентификации модели множественной регрессии 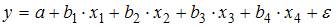 количество оцениваемых параметров равно …
количество оцениваемых параметров равно …
Решение:
При оценке модели множественной регрессии 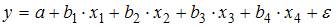 рассчитываются следующие параметры: свободный член a и четыре параметра при независимых переменных х. Итого 5 параметров.
рассчитываются следующие параметры: свободный член a и четыре параметра при независимых переменных х. Итого 5 параметров.
Тема 2: Отбор факторов, включаемых в модель множественной регрессии
1. В модели множественной регрессии  определитель матрицы парных коэффициентов корреляции между факторами
определитель матрицы парных коэффициентов корреляции между факторами 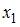 ,
, 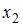 и
и 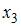 близок к единице. Это означает, что факторы
близок к единице. Это означает, что факторы 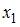 ,
, 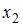 и
и 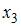 …
…
независимы
мультиколлинеарны
количественно измеримы
значимы
Решение:
Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами. Если факторы не коррелированы между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной. Поскольку все недиагональные элементы 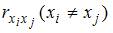 были бы равны нулю.
были бы равны нулю.
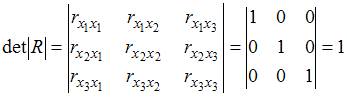 , поскольку
, поскольку  =
=  =
=  и
и  =
=  =
= 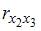 =0.
=0.
Если между факторами существует полная линейная зависимость и все коэффициенты парной корреляции равны единице, то определитель такой матрицы равен нулю.
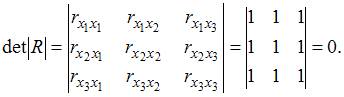
Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.
2. При моделировании линейного уравнения множественной регрессии вида 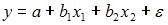 необходимо, чтобы выполнялось требование отсутствия взаимосвязи между …
необходимо, чтобы выполнялось требование отсутствия взаимосвязи между …
x1 и x2
y и {x1; x2}
a и {b1; b2}
b1 и b2
Решение:
Эконометрическая модель уравнения регрессии может быть представлена линейным уравнением множественной регрессии в виде выражения 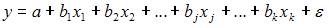 , где y – зависимая переменная; xj – независимая переменная (j = 1,…, k; k – количество независимых переменных); a, bj – параметры (a – свободный член уравнения, bj – коэффициент регрессии);
, где y – зависимая переменная; xj – независимая переменная (j = 1,…, k; k – количество независимых переменных); a, bj – параметры (a – свободный член уравнения, bj – коэффициент регрессии); 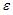 – случайные факторы. При построении модели множественной регрессии необходимо исключить возможность существования тесной линейной зависимости между независимыми (объясняющими) переменными, которая ведет к проблеме мультиколлинеарности. Поэтому в данной модели необходимо, чтобы выполнялось требование отсутствия взаимосвязи между x1 и x2.
– случайные факторы. При построении модели множественной регрессии необходимо исключить возможность существования тесной линейной зависимости между независимыми (объясняющими) переменными, которая ведет к проблеме мультиколлинеарности. Поэтому в данной модели необходимо, чтобы выполнялось требование отсутствия взаимосвязи между x1 и x2.
