Теорема взаимности

Пусть имеются два источника (на рис.5 изображены линии тока). Запишем по паре уравнений Максвелла для каждого из них:

рис 5

Скалярно умножив первое уравнение на

Н₂, а третье - на Е₁, и вычтя одно из другого, найдем:

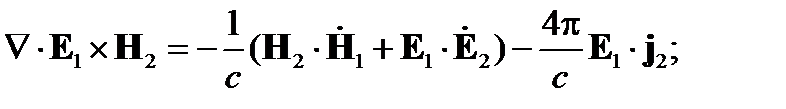
Для второй пары уравнений Максвелла (она получается заменой индексов 1 на 2 и 2 на 1), проделав то же самое, получим:

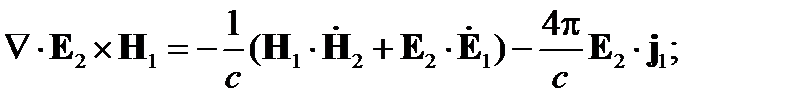
Здесь левые части уравнений представлены так же, как в § 11.

Для монохроматического поля (пропорционального 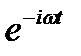) заменой 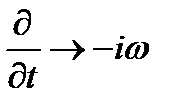получим:

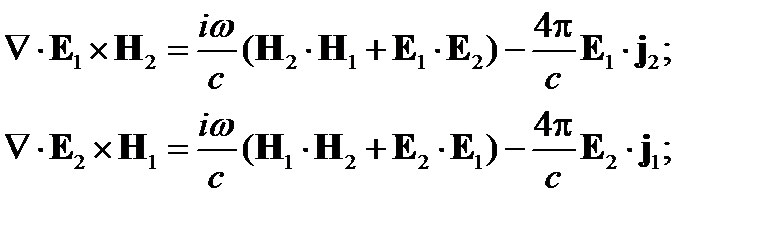
Вычтем из первого уравнения второе:

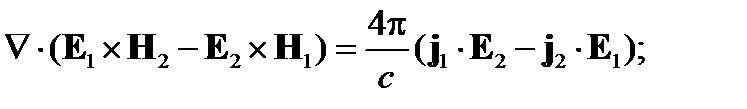
Применив теорему Гаусса, найдем:

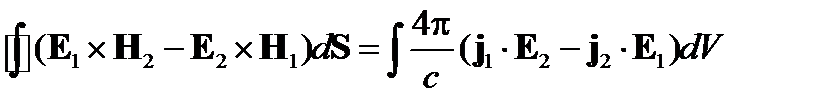
Интеграл в левой части стремится к нулю на бесконечности вследствие естественных потерь энергии. Поэтому будем считать, что поле на гра­нице отсутствует. Это дает:

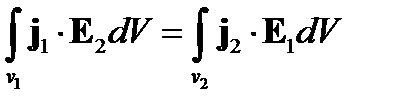
Учтя связь

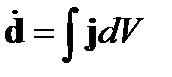
и выбрав j в виде

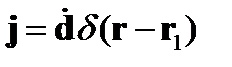
приведем теорему взаимности к виду

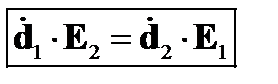
Основные понятия макроэлектродинамики

Объектом исследований макроскопической электродинамики яв­ляются электромагнитные поля в пространстве, заполненном вещест­вом. Макроэлектродинамика оперирует усредненными величинами, не интересуясь микроскопическими флуктуациями этих величин, связан­ными с молекулярным строением вещества.

Рассмотрим модель сплошной среды. При переходе от реальной среды к сплошной должны сохраняться макроскопические условия:

1. всевозможные граничные условия;

2. геометрия среды;

3. внешние источники поля.

Усреднение можно производить либо по объему и времени, либо статистически (по ансамблю).

Статистическое усреднение, в отличие от усреднения по объему и

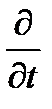времени, всегда коммутативно с операторами и . При этом целесообразно ввести параметр неоднородности поля - расстояние, на кото­ром поле изменяется существенно.

Обозначим индексом “м” точные микроскопические значения по­лей Е и Н, потенциалов А и 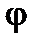, а также плотности всех зарядов 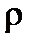и

всех токов j:

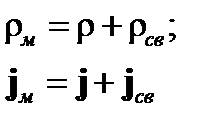
Уравнения поля в сплошной среде получаются усреднением урав­нений (1) для электромагнитного поля в вакууме, где вместо 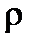и j сто­ят 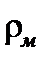и ^: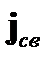

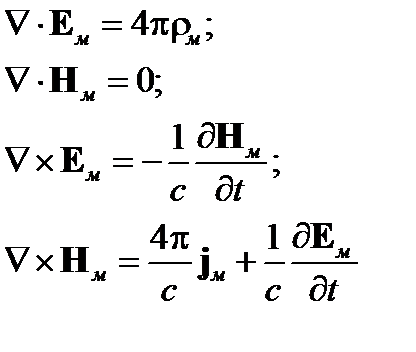(17)

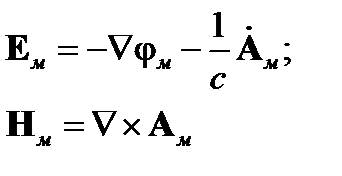
Произведем усреднение этих уравнений (<..> - усреднение по ан­самблю), причем

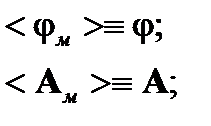
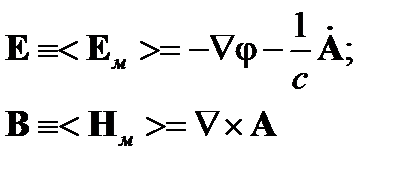
Тогда из (17) получим:

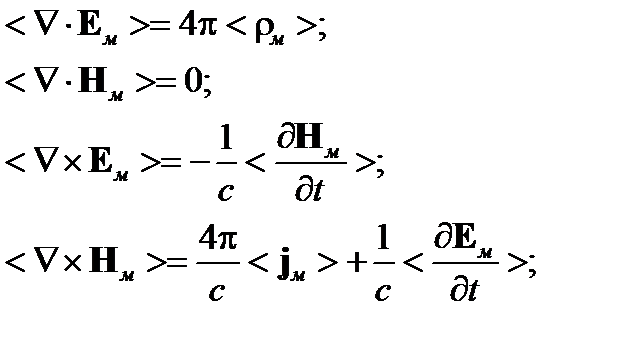
Далее с учетом коммутативности различных операторов и опера­ции усреднения, запишем:

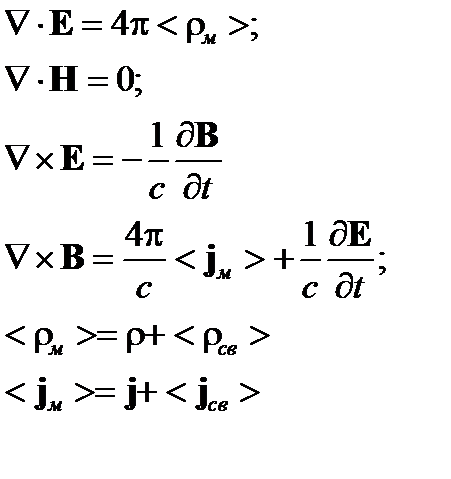(18)

Здесь р и j не усредняются, так как входят в макроскопические усло­вия и не являются статистическими параметрами.

Определим связанные источники:

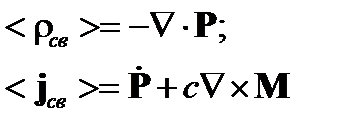
Р и М - электрическая и магнитная поляризации.

Определим поля D и Н:

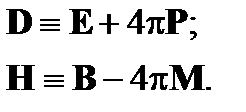
Тогда (18) перепишем в виде

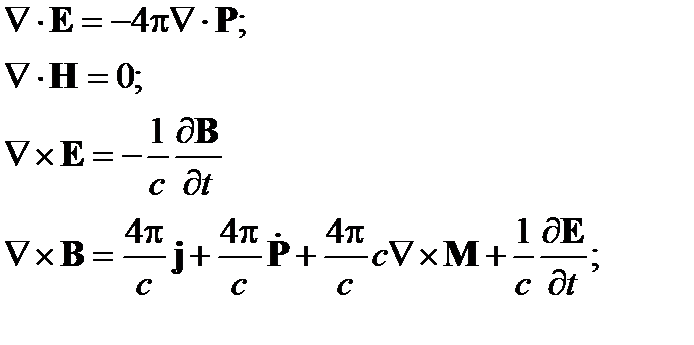(19)

Для первого и последнего уравнений (19) получим:

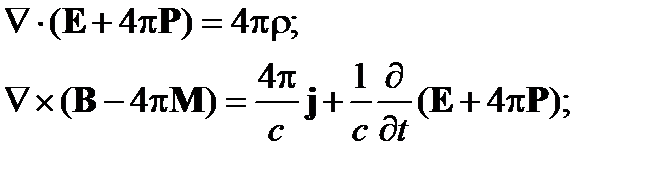
Окончательно запишем:

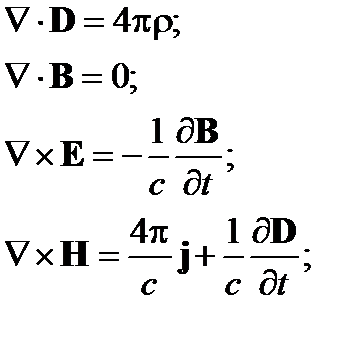(20)

Для полноты системы уравнений (20) необходимы уравнения связи:

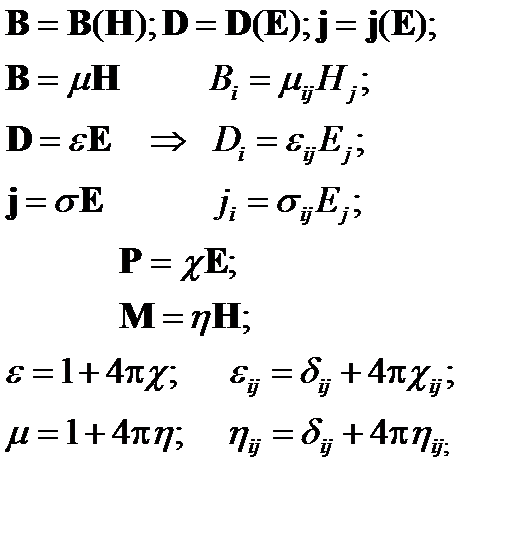
Здесь 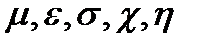- тензоры второго ранга материальных характеристик среды.