Погрешность корней скалярных уравнений с приближенными коэффициентами
Пусть решается алгебраическое или трансцендентное уравнение вида
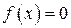 (4.10)
(4.10)
Это уравнение, являясь нелинейным, может иметь один или несколько корней или не иметь их вовсе. Каждый корень так или иначе зависит от числовых данных уравнения (4.10). Эти числовые данные (будем иногда называть их коэффициентами уравнения) можно считать фиксированными значениями параметров, т.е. уравнение (4.10) целесообразно рассматривать в качестве представителя семейства уравнений
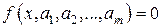 (4.11)
(4.11)
и наличие корней у (4.10) связывать с существованием неявной функции 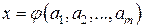 при данном наборе значений параметров (коэффициентов)
при данном наборе значений параметров (коэффициентов) 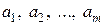 . Поскольку эти числа, как правило, точно не известны (грубость модели, неточность измерений, усечение чисел при вводе в ЭВМ и т.п.), встает вопрос о том, как влияет погрешность коэффициентов уравнения (4.10) на погрешность его корней.
. Поскольку эти числа, как правило, точно не известны (грубость модели, неточность измерений, усечение чисел при вводе в ЭВМ и т.п.), встает вопрос о том, как влияет погрешность коэффициентов уравнения (4.10) на погрешность его корней.
Реально можно оценить лишь главную часть погрешности корня, понимая под ней, как и в § 4.1, модуль дифференциала. Если 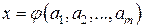 – корень уравнения (4.11), то линейная часть его измерения, соответствующая изменениям аргументов – коэффициентов
– корень уравнения (4.11), то линейная часть его измерения, соответствующая изменениям аргументов – коэффициентов 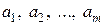 , равна
, равна
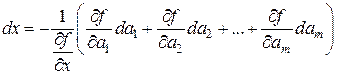 .
.
Переходя здесь к модулям и заменяя истинные абсолютные погрешности коэффициентов 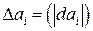 их оценками
их оценками 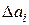 , получим формулу для оценки абсолютной погрешности корня:
, получим формулу для оценки абсолютной погрешности корня:
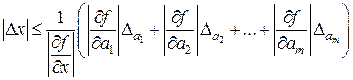 . (4.12)
. (4.12)
Заметим, что при вычислении значений частных производных в (4.12) следует пользоваться фиксированными значениями коэффициентов 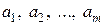 (такими, какими они используются при нахождении корня) и приближенным значением того корня, степень неопределенности которого устанавливается. Ясно, что для разных корней одного и того же уравнения значения этой величины могут сильно различаться.
(такими, какими они используются при нахождении корня) и приближенным значением того корня, степень неопределенности которого устанавливается. Ясно, что для разных корней одного и того же уравнения значения этой величины могут сильно различаться.
Получаемую с помощью (4.12) оценку будем называть безусловной абсолютной погрешностью приближенного корня 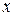 уравнения (4.11) с приближенными коэффициентами и обозначать б.п.
уравнения (4.11) с приближенными коэффициентами и обозначать б.п. 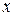 . Это же
. Это же 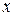 есть точный корень уравнения (4.10), в то время как при численном решении уравнения вместо
есть точный корень уравнения (4.10), в то время как при численном решении уравнения вместо 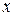 будет получено некоторое приближение к нему
будет получено некоторое приближение к нему 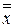 . Возникающую при этом остаточную погрешность или погрешность метода назовем условной погрешностью и обозначим у.п.
. Возникающую при этом остаточную погрешность или погрешность метода назовем условной погрешностью и обозначим у.п. 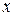 .
.
Полная погрешность корня уравнения с приближенными коэффициентами складывается из погрешностей условной и безусловной. Так как величиной условной погрешности распоряжается вычислитель, причем ее уменьшение в разумных пределах не вызывает, как правило, больших затруднений, то обычно, чтобы не увеличивать полную погрешность корня приближенного уравнения, условную погрешность задают неравенством
у.п. 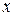
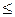 б.п.
б.п. 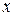 (4.13)
(4.13)
или даже
у.п. 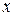
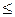 0.1 б.п.
0.1 б.п. 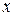
Если воспользоваться правилом Ньютона оценки близости приближенного корня (нуля) 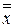 дифференцируемой функции
дифференцируемой функции 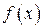 к точному корню
к точному корню 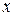
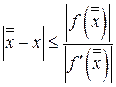 (4.14)
(4.14)
и оценкой (4.12), то можно на основе (4.13) получить простой критерий окончания процесса численного решения скалярного уравнения (4.10) с приближенными коэффициентами:
уточнение корня 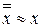 ведется до тех пор, пока не выполнится условие
ведется до тех пор, пока не выполнится условие
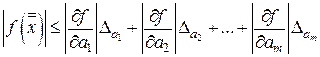 . (4.15)
. (4.15)
Как видим, большýю роль в неравенстве (4.15) играют модули частных производных данной функции по параметрам, называемые коэффициентами чувствительности.
