Метрика и внутренняя геометрия
Вновь рассмотрим гладкую кривую:
.
Элемент её длины определяется из соотношения:
,
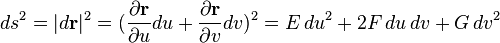где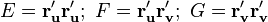 
.
Эта квадратичная форма называется первой квадратичной формой и представляет собой двумерный вариант метрики поверхности. Для регулярной поверхности её дискриминант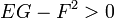 
во всех точках. Коэффициент 
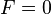в точке поверхности тогда и только тогда, когда в этой точке координатные кривые ортогональны. В частности, на плоскости с декартовыми координатами 
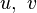получается метрика 
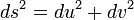(теорема Пифагора).
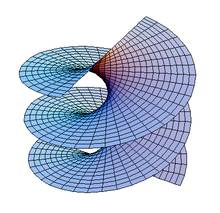
Геликоид
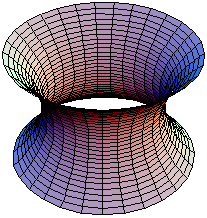
Катеноид
Метрика не определяет однозначно форму поверхности. Например, метрикигеликоида икатеноида, параметризованных соответствующим образом, совпадают, то есть между их областями существует соответствие, сохраняющее все длины (изометрия). Свойства, сохраняющиеся при изометрических преобразованиях, называются внутренней геометрией поверхности. Внутренняя геометрия не зависит от положения поверхности в пространстве и не меняется при её изгибании без растяжения и сжатия (например, при изгибании цилиндра в конус)[1].
Метрические коэффициенты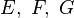 
определяют не только длины всех кривых, но и вообще результаты всех измерений внутри поверхности (углы, площади, кривизна и др.). Поэтому всё, что зависит только от метрики, относится к внутренней геометрии.
[править]Нормаль и нормальное сечение
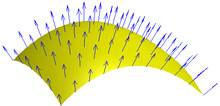
Векторы нормали в точках поверхности
Одной из основных характеристик поверхности является её нормаль — единичный вектор, перпендикулярный касательной плоскости в заданной точке:
.
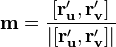Знак нормали зависит от выбора координат.
Сечение поверхности плоскостью, содержащей нормаль (в данной точке), образует некоторую кривую на поверхности, которая называется нормальным сечением поверхности. Главная нормаль для нормального сечения совпадает с нормалью к поверхности (с точностью до знака).
Если же кривая на поверхности не является нормальным сечением, то её главная нормаль образует с нормалью поверхности некоторый угол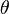 
. Тогда кривизна 
кривой связана с кривизной 
нормального сечения (с той же касательной) формулой Мёнье:
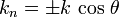
Координаты орта нормали для разных способов задания поверхности приведены в таблице:
| Координаты нормали в точке поверхности | |
| неявное задание |  |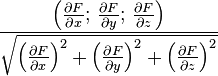
| явное задание |  |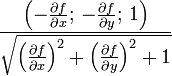
| параметрическое задание |  |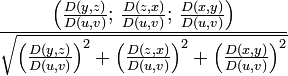
Здесь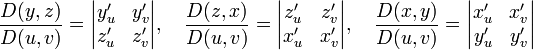 
.
Все производные берутся в точке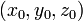 
.