Оценка эффективности методов распознавания

Получение контрольных и обучающих выборок

Используя генератор случайных чисел пакета MathCad можно создать как обучающие, так и контрольные выборки с любым объемом и любой размерности пространства информативных признаков. Пример листа MathCad, в котором создается выборка из 28 объектов с нормально распределенным законом распределения признаков (признаковое пространство четырехмерное) показан на рис. 1.1.

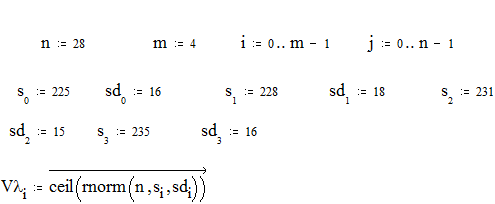Рис. 1.1. Лист MathCad с генератором случайных чисел

Каждый информативный признак в выборке представлен вектором-столбцом Vλ из 28 элементов. Случайные числа, распределенные по нормальному закону распределения, генерируются функцией

rnorm(n, s, sd),

где n-число элементов в выборке, s – математическое ожидание информативного признака, sd -дисперсия информативного признака.

Варьируя эти параметры (s и sd) вы можете менять структуру распределения классов в признаковом пространстве и исследовать эффективность классификации при различных классовых структурах.

Функция ceil округляет случайное число до ближайшего целого.

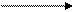Значок обозначает операцию векторизации, то есть одновременное выполнение скалярной операции над всеми элементами вектора.

Пример полученной выборки в четырехмерном признаковом пространстве показан на рис. 1.2.

Рис. 1.2. Пример выборки из 28 элементов в четырехмерном признаковом пространстве.

Порядок построения линейной разделяющей гиперплоскости

По полученным обучающим выборкам найдем разделяющую гиперплоскость, которая проходит через середину отрезка, соединяющего центроиды двух обучающих выборок и перпендикулярна к нему.

Построим линейную разделяющую поверхность для двух классов.

Если вектор X_i характеризует i-й объект первого класса, а вектор Y_j характеризует j–й объект второго класса, то координаты центроид А и B , а, следовательно, и отрезка AB, их соединяющего, определяются как

М[x] и М[y].

координаты точки С, которая лежит на середине отрезка AB, определяются по формуле

(М[x1] + М[y1])/2; (М[x2] + М[y2])/2;… (М[xn] + М[yn])/2),

где n –число информативных признаков или размерность признакового пространства.

Если плоскость перпендикулярна вектору n(a; b; c), например, в трехмерном пространстве, то уравнение плоскости в этом пространстве записывается как

ax + by + cz + d = 0

Уравнение плоскости, перпендикулярной вектору n(a; b; c) и проходящей через точку (x0; y0; z0) записывается как

a(x − x0) + b(y − y0) + c(z − z0) + d = 0.

Чтобы перейти от вектора AB к вектору n, необходимо из координат М[xi] вычесть координаты М[yi], то есть из координат точки а вычесть координаты точки B.

Дискриминантный анализ

Основная цель

Дискриминантный анализ используется для принятия решения о том, какие переменные различают (дискриминируют) две или более возникающие совокупности (группы) [1]. Например, некий исследователь в области образования может захотеть исследовать, какие переменные относят выпускника средней школы к одной из трех категорий: (1) поступающий в колледж, (2) поступающий в профессиональную школу или (3) отказывающийся от дальнейшего образования или профессиональной подготовки. Для этой цели исследователь может собрать данные о различных переменных, связанных с учащимися школы. После выпуска большинство учащихся, естественно, должно попасть в одну из названных категорий. Затем можно использовать Дискриминантный анализ для определения того, какие переменные дают наилучшее предсказание выбора учащимися дальнейшего пути.

Медик может регистрировать различные переменные, относящиеся к состоянию больного, чтобы выяснить, какие переменные лучше предсказывают, что пациент, вероятно, выздоровел полностью (группа 1), частично (группа 2) или совсем не выздоровел (группа 3). Биолог может записать различные характеристики сходных типов (групп) цветов, чтобы затем провести анализ дискриминантной функции, наилучшим образом разделяющей типы или группы.

Классификация

Другой главной целью применения дискриминантного анализаявляется проведение классификации. Как только модель установлена и получены дискриминирующие функции, возникает вопрос о том, как хорошо они могут предсказывать, к какой совокупности принадлежит конкретный образец?

Априорная и апостериорная классификация.Прежде чем приступить к изучению деталей различных процедур оценивания, важно уяснить, что эта разница ясна. Обычно, если вы оцениваете на основании некоторого множества данных дискриминирующую функцию, наилучшим образом разделяющую совокупности, и затем используете те же самые данные для оценивания того, какова точность вашей процедуры, то вы во многом полагаетесь на волю случая. В общем случае, получают, конечно худшую классификацию для образцов, не использованных для оценки дискриминантной функции. Другими словами, классификация действует лучшим образом для выборки, по которой была проведена оценка дискриминирующей функции (апостериорная классификация), чем для свежей выборки (априорная классификация). Трудности с (априорной) классификацией будущих образцов заключается в том, что никто не знает, что может случиться. Намного легче классифицировать уже имеющиеся образцы. Поэтому оценивание качества процедуры классификации никогда не производят по той же самой выборке, по которой была оценена дискриминирующая функция. Если желают использовать процедуру для классификации будущих образцов, то ее следует "испытать" (произвести кросс-проверку) на новых объектах.

Функции классификации.Функции классификации не следует путать с дискриминирующими функциями. Функции классификации предназначены для определения того, к какой группе наиболее вероятно может быть отнесен каждый объект. Имеется столько же функций классификации, сколько групп. Каждая функция позволяет вам для каждого образца и для каждой совокупности вычислить веса классификации по формуле:

S_i = c_i + w_i1*x₁ + w_i2*x₂ + ... + w_im*x_m

В этой формуле индекс i обозначает соответствующую совокупность, а индексы 1, 2, ..., m обозначают m переменных; c_i являются константами для i-ой совокупности, w_ij - веса для j-ой переменной при вычислении показателя классификации для i-ой совокупности; x_j - наблюдаемое значение для соответствующего образца j-ой переменной. Величина S_i является результатом показателя классификации.

Поэтому вы можете использовать функции классификации для прямого вычисления показателя классификации для некоторых новых значений.

Классификация наблюдений.Как только вы вычислили показатели классификации для наблюдений, легко решить, как производить классификацию наблюдений. В общем случае наблюдение считается принадлежащим той совокупности, для которой получен наивысший показатель классификации (кроме случая, когда вероятности априорной классификации становятся слишком малыми; см. ниже). Поэтому, если вы изучаете выбор карьеры или образования учащимися средней школы после выпуска (поступление в колледж, в профессиональную школу или получение работы) на основе нескольких переменных, полученных за год до выпуска, то можете использовать функции классификации, чтобы предсказать, что наиболее вероятно будет делать каждый учащийся после выпуска. Однако вы хотели бы определить вероятность, с которой учащийся сделает предсказанный выбор. Эти вероятности называются апостериорными, и их также можно вычислить. Однако для понимания, как эти вероятности вычисляются, вначале рассмотрим так называемое расстояние Махаланобиса.

Расстояние Махаланобиса.В общем, расстояние Махаланобиса является мерой расстояния между двумя точками в пространстве, определяемым двумя или более коррелированными переменными. Например, если имеются всего две некоррелированных переменные, то вы можете нанести точки (образцы) на стандартную 2М диаграмму рассеяния. Расстояние Махаланобиса между точками будет в этом случае равно расстоянию Евклида, т.е. расстоянию, измеренному, например, рулеткой. Если имеются три некоррелированные переменные, то для определения расстояния вы можете по-прежнему использовать рулетку (на 3М диаграмме). При наличии более трех переменных вы не можете более представить расстояние на диаграмме. Также и в случае, когда переменные коррелированы, то оси на графике могут рассматриваться как неортогональные (они уже не направлены под прямыми углами друг к другу). В этом случае простое определение расстояния Евклида не подходит, в то время как расстояние Махаланобиса является адекватно определенным в случае наличия корреляций.

Расстояние Махаланобиса и классификация.Для каждой совокупности в выборке вы можете определить положение точки, представляющей средние для всех переменных в многомерном пространстве, определенном переменными рассматриваемой модели. Эти точки называются центроидами группы. Для каждого наблюдения вы можете затем вычислить его расстояние Махаланобиса от каждого центроида группы. Снова, вы признаете наблюдение принадлежащим к той группе, к которой он ближе, т.е. когда расстояние Махаланобиса до нее минимально.

Апостериорные вероятности классификации.Используя для классификации расстояние Махаланобиса, вы можете теперь получить вероятность того, что образец принадлежит к конкретной совокупности. Это значение будет не вполне точным, так как распределение вокруг среднего для каждой совокупности будет не в точности нормальным. Так как принадлежность каждого образца вычисляется по априорному знанию модельных переменных, эти вероятности называются апостериорными вероятностями. Короче, апостериорные вероятности - это вероятности, вычисленные с использованием знания значений других переменных для образцов из частной совокупности. Некоторые пакетыавтоматически вычисляют эти вероятности для всех наблюдений (или для выбранных наблюдений при проведении кросс-проверки).

Априорные вероятности классификации.Имеется одно дополнительное обстоятельство, которое следует рассмотреть при классификации образцов. Иногда вы знаете заранее, что в одной из групп имеется больше наблюдений, чем в другой. Поэтому априорные вероятности того, что образец принадлежит такой группе, выше. Например, если вы знаете заранее, что 60% выпускников вашей средней школы обычно идут в колледж, (20% идут в профессиональные школы и остальные 20% идут работать), то вы можете уточнить предсказание таким образом: при всех других равных условиях более вероятно, что учащийся поступит в колледж, чем сделает два других выбора. Вы можете установить различные априорные вероятности, которые будут затем использоваться для уточнения результатов классификации наблюдений (и для вычисления апостериорных вероятностей).

На практике, исследователю необходимо задать себе вопрос, является ли неодинаковое число наблюдений в различных совокупностях в первоначальной выборке отражением истинного распределения в популяции, или это только (случайный) результат процедуры выбора. В первом случае вы должны положить априорные вероятности пропорциональными объемам совокупностей в выборке; во втором - положить априорные вероятности одинаковыми для каждой совокупности. Спецификация различных априорных вероятностей может сильно влиять на точность классификации.

Итог классификации.Общим результатом, на который следует обратить внимание при оценке качества текущей функции классификации, является матрица классификации. Матрица классификации содержит число образцов, корректно классифицированных (на диагонали матрицы) и тех, которые попали не в свои совокупности (группы).

Другие предостережения.При повторной итерации апостериорная классификация того, что случилось в прошлом, не очень трудна. Нетрудно получить очень хорошую классификацию тех образцов, по которым была оценена функция классификации. Для получения сведений, насколько хорошо работает процедура классификации на самом деле, следует классифицировать (априорно) различные наблюдения, то есть, наблюдения, которые не использовались при оценке функции классификации. Вы можете гибко использовать условия отбора для включения или исключения из вычисления наблюдений, поэтому матрица классификации может быть вычислена по "старым" образцам столь же успешно, как и по "новым". Только классификация новых наблюдений позволяет определить качество функции классификации (см. также кросс-проверку); классификация старых наблюдений позволяет лишь провести успешную диагностику наличия выбросов или области, где функция классификации кажется менее адекватной.

Итог.В общем, Дискриминантный анализ - это очень полезный инструмент для поиска переменных, позволяющих относить наблюдаемые объекты в одну или несколько реально наблюдаемых групп, (2) - для классификации наблюдений в различные группы.

Оценка эффективности методов распознавания

В качестве расчетных показателей качества диагностических решающих правил используется: диагностическая чувствительность (ДЧ), диагностическая специфичность (ДС), прогностическая значимость положительных результатов (ПЗ⁺), прогностическая значимость отрицательных результатов (ПЗ^-), диагностическая эффективность решающего правила (ДЭ) [2].

Эти показатели вычислялись по данным таблицы распределений результатов контрольных испытаний (табл. 4.1).

Таблица 3 - Таблица контрольных испытаний

Обследуемые	Результаты срабатывания правил	Всего
положительные	отрицательные
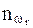	ИП	ЛО	ИП+ЛО
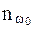	ЛП	ИО	ЛП+ИО
Всего	ИП+ЛП	ЛО+ИО	ИП+ЛП+ЛО+ИО

r – номер класса исследуемого заболевания; 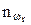- количество людей в контрольной выборке в исследуемом классе заболеваний; 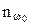- количество здоровых людей в контрольной выборке; ИП – истинно положительный результат равный количеству людей класса 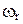правильно классифицируемых рассматриваемым правилом; ЛП – ложно положительный результат равный количеству людей класса 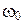ошибочно отнесенных решающим правилом к классу 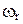; ЛО – ложно отрицательный результат: количество людей класса 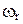ошибочно отнесенных решающим правилом к классу 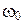; ИО – истинно отрицательный результат: количество людей класса 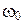правильно классифицируемых решающим правилом.

Для приведенных в таблице 3 обозначений расчет показателей качества осуществляется в соответствии с выражениями:

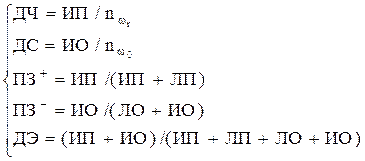(1)