Корректность компактных операторов
Определение. Линейный оператор 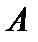 , отображающий банахово пространство
, отображающий банахово пространство 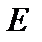 в себя (или другое банахово пространство), называется компактным (вполне непрерывным), если каждое ограниченное множество он переводит в предкомпактное.
в себя (или другое банахово пространство), называется компактным (вполне непрерывным), если каждое ограниченное множество он переводит в предкомпактное.
Комментарий. Напомним, что множество 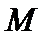 метрического пространства
метрического пространства 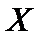 компактно, если из любого бесконечного его подмножества можно выделить последовательность, сходящуюся к элементу из
компактно, если из любого бесконечного его подмножества можно выделить последовательность, сходящуюся к элементу из 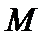 , и предкомпактно, если замыкание
, и предкомпактно, если замыкание 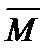 компактно. Если линейный оператор
компактно. Если линейный оператор 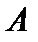 компактен, то он переводит любую ограниченную последовательность
компактен, то он переводит любую ограниченную последовательность 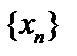 в компактную последовательность
в компактную последовательность 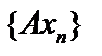 , то есть из любой подпоследовательности последовательности
, то есть из любой подпоследовательности последовательности 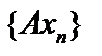 можно выделить сходящуюся подпоследовательность. Компактность и предкомпактность
можно выделить сходящуюся подпоследовательность. Компактность и предкомпактность  это прежде всего свойства пространств. Суть компактности
это прежде всего свойства пространств. Суть компактности  в исчерпываемости некого бесконечномерного пространства конечномерным приближением с любой наперед заданной точностью. Компактный оператор наследует свойства конечномерного оператора в том смысле, что всегда может быть приближен им.
в исчерпываемости некого бесконечномерного пространства конечномерным приближением с любой наперед заданной точностью. Компактный оператор наследует свойства конечномерного оператора в том смысле, что всегда может быть приближен им.
Теорема1. Компактный оператор 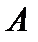 всегда ограничен.
всегда ограничен.
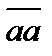 . Пустькомпактный оператор
. Пустькомпактный оператор 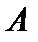 не ограничен. Тогда найдется последовательность
не ограничен. Тогда найдется последовательность 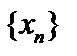 , такая, что
, такая, что 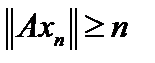 |. Но тогда из неё нельзя выделить сходящуюся подпоследовательность, что противоречит тому, что
|. Но тогда из неё нельзя выделить сходящуюся подпоследовательность, что противоречит тому, что 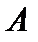
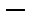 вполне непрерывный оператор.
вполне непрерывный оператор. 
Комментарий. Не любой непрерывный линейный оператор вполне непрерывен.Рассмотрим, например, единичный оператор 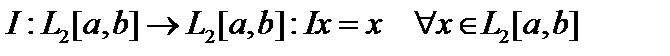 . Он, очевидно, ограничен, но не компактен. Покажем это.
. Он, очевидно, ограничен, но не компактен. Покажем это.
 В пространстве
В пространстве 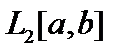 существует бесконечная ортонормированная система (ОНС)
существует бесконечная ортонормированная система (ОНС) 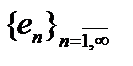 , такая, что
, такая, что 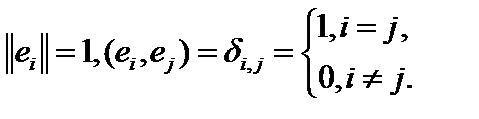 . Ясно, что последовательность
. Ясно, что последовательность 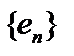 лежит на сфере
лежит на сфере 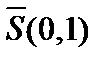 , то есть она ограничена, но из неё нельзя выделить сходящуюся подпоследовательность, так как
, то есть она ограничена, но из неё нельзя выделить сходящуюся подпоследовательность, так как 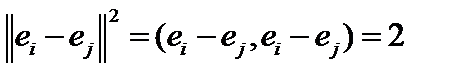 . То есть единичная сфера
. То есть единичная сфера 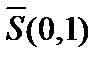 в гильбертовом пространстве– замкнутое и ограниченное множество, но не компакт, а
в гильбертовом пространстве– замкнутое и ограниченное множество, но не компакт, а 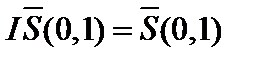 . Таким образом, единичный оператор
. Таким образом, единичный оператор 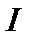 не компактен.
не компактен. 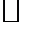
Можно показать, что единичный оператор 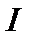 в любом бесконечномерном банаховом пространстве
в любом бесконечномерном банаховом пространстве 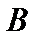 не компактен. Это следует из теоремы Рисса о некомпактности единичного шара в бесконечномерном
не компактен. Это следует из теоремы Рисса о некомпактности единичного шара в бесконечномерном 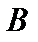 - пространстве.
- пространстве.
Теорема 2.Если 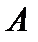 – компактный оператор,
– компактный оператор, 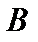 – ограниченный в банаховом пространстве
– ограниченный в банаховом пространстве 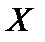 , то операторы
, то операторы 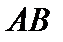 и
и 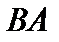 – компактны.
– компактны.
 Если множество
Если множество 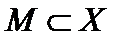 ограничено, то множество
ограничено, то множество 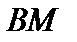 тоже ограничено. Следовательно, множество
тоже ограничено. Следовательно, множество 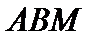 предкомпактно, а это и означает, что оператор
предкомпактно, а это и означает, что оператор 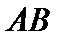 компактен. Далее, если
компактен. Далее, если 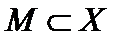 ограничено, то
ограничено, то 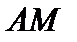 предкомпактно, а тогда в силу непрерывности
предкомпактно, а тогда в силу непрерывности 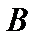 множество
множество 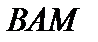 тоже предкомпактно, то есть оператор
тоже предкомпактно, то есть оператор 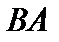 компактен.
компактен. 
Пространства функционалов
Определение 1. Линейным функционалом в гильбертовом пространстве H называется линейный оператор, отображающий H во множество чисел (вещественных или комплексных). Поскольку линейный функционал является оператором, то для него определено понятие непрерывности, нормы и справедливы все свойства операторов.
Определение 2. Ядром линейного функционала f, определенного в H, называется совокупность всех векторов 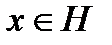 ,для которых f(x)=0. Ядро функционала f обозначается через
,для которых f(x)=0. Ядро функционала f обозначается через 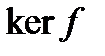 .
.
Теорема 1. Если f -- линейный функционал в H, то 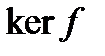 является подпространством в H.
является подпространством в H.
 Покажем, что любая линейная комбинация произвольных двух векторов
Покажем, что любая линейная комбинация произвольных двух векторов 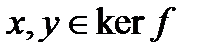 лежит в
лежит в 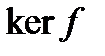 .Но если
.Но если 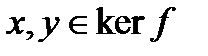 ,то
,то 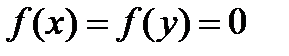 , а значит, для любых чисел
, а значит, для любых чисел 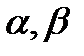 имеем
имеем 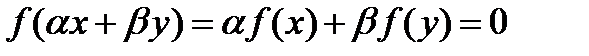 .Следовательно,
.Следовательно, 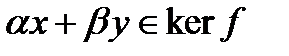 .
. 
Теорема 2. Ядро непрерывного линейного функционала замкнуто.
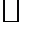 Пусть произвольная последовательность векторов из
Пусть произвольная последовательность векторов из 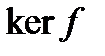 ,
, 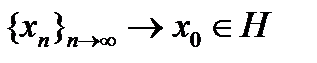 . Поскольку линейный функционал f непрерывен, то
. Поскольку линейный функционал f непрерывен, то 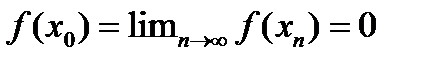 , а значит
, а значит 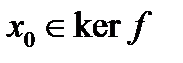 .Следовательно, ядро f замкнуто.
.Следовательно, ядро f замкнуто. 
Определение 3. Коразмерностью подпространства S называется размерность его ортогонального дополнения 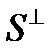 .
.
Теорема 3. Коразмерность ядра ненулевого непрерывного функционала f равна единице.
 Гильбертово пространство H может быть представлено в виде прямой суммы замкнутого подпространства S и его ортогонального дополнения
Гильбертово пространство H может быть представлено в виде прямой суммы замкнутого подпространства S и его ортогонального дополнения 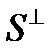 :
: 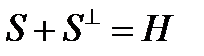 . Это означает, что для любого вектора
. Это означает, что для любого вектора 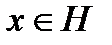 найдутся, и притом единственным образом, векторы
найдутся, и притом единственным образом, векторы 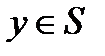 и
и 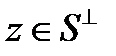 такие, что
такие, что 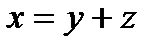 . Поскольку функционал f непрерывен, то его ядро
. Поскольку функционал f непрерывен, то его ядро 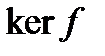 замкнуто и, следовательно, все пространство H представляется в виде прямой суммы ядра
замкнуто и, следовательно, все пространство H представляется в виде прямой суммы ядра 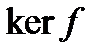 и его ортогонального дополнения
и его ортогонального дополнения 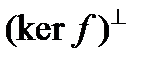 :
: 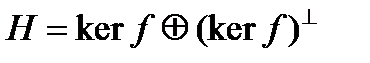 . Последнее означает, что каждый вектор
. Последнее означает, что каждый вектор 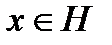 может быть единственным образом представлен в виде
может быть единственным образом представлен в виде 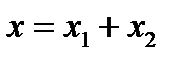 , где
, где 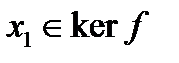 , а
, а  . С другой стороны, функционал f не равен нулю, а значит
. С другой стороны, функционал f не равен нулю, а значит 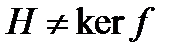 . Следовательно, ортогональное дополнение к ядру содержит не только нулевой вектор. Пусть
. Следовательно, ортогональное дополнение к ядру содержит не только нулевой вектор. Пусть  и
и 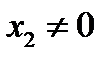 . Рассмотрим произвольный вектор
. Рассмотрим произвольный вектор 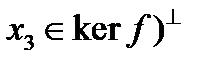 и положим
и положим 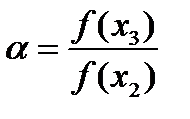 и
и 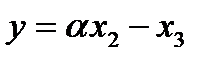 . Тогда, с одной стороны,
. Тогда, с одной стороны, 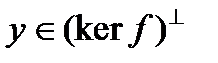 , так как вектор
, так как вектор 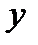 является линейной комбинацией векторов
является линейной комбинацией векторов  и
и 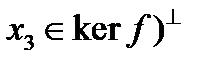 . Но с другой
. Но с другой 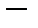
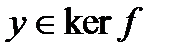 так как
так как 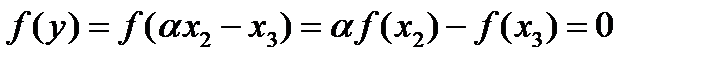 .Следовательно,
.Следовательно, 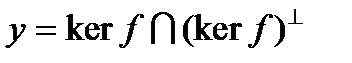 . Поэтому
. Поэтому 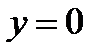 и
и 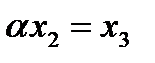 . Таким образом, любой вектор из
. Таким образом, любой вектор из 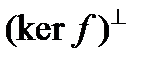 пропорционален вектору
пропорционален вектору 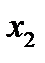 . Это и означает, что коразмерность ядра равна единице.
. Это и означает, что коразмерность ядра равна единице. 
Теорема 4. Если ядро функционала замкнуто, то он непрерывен.
 Если ядро функционала совпадает со всем пространством, то функционал равен нулю и, очевидно, непрерывен. Если ядро функционала f является замкнутым подпространством, не совпадающим со всем пространством H, то ортогональное дополнение к ядру содержит хоть один ненулевой вектор
Если ядро функционала совпадает со всем пространством, то функционал равен нулю и, очевидно, непрерывен. Если ядро функционала f является замкнутым подпространством, не совпадающим со всем пространством H, то ортогональное дополнение к ядру содержит хоть один ненулевой вектор 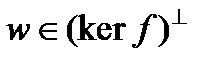 . Произвольным образом выберем последовательность
. Произвольным образом выберем последовательность 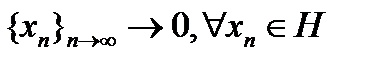 . Поскольку
. Поскольку 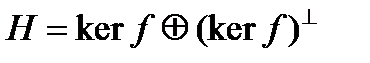 , а значит
, а значит 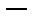 для каждого номера n найдутся векторы
для каждого номера n найдутся векторы 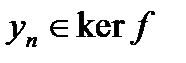 и
и  такие, что
такие, что 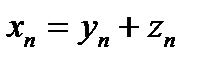 . Далее, каждый из векторов
. Далее, каждый из векторов 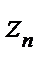 представим в виде
представим в виде 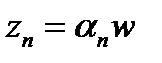 . Поскольку, с одной стороны,
. Поскольку, с одной стороны, 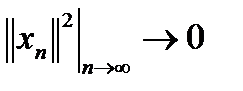 , а с другой
, а с другой 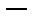
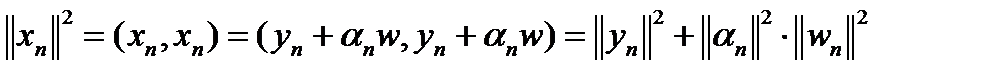 . Сумма двух неотрицательных слагаемых в пределе равна нулю, а вектор
. Сумма двух неотрицательных слагаемых в пределе равна нулю, а вектор 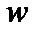 ненулевой, то есть так как
ненулевой, то есть так как 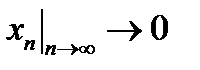 , то
, то 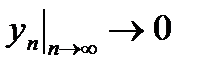 , и
, и 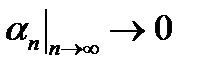 . Следовательно,
. Следовательно, 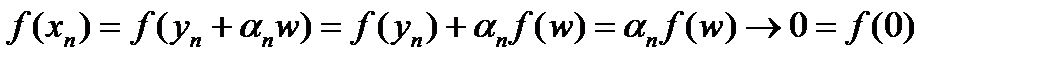 при
при  . Значит, линейный функционал f непрерывен в нуле и поэтому непрерывен всюду.
. Значит, линейный функционал f непрерывен в нуле и поэтому непрерывен всюду. 
Определение 4. Множество непрерывных линейных функционалов, определенных в гильбертовом пространстве H, называется пространством, сопряженным к H, и обозначается через H*. Очевидно, что H* 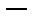 линейное пространство.
линейное пространство.
Теорема 5 (Ф. Рисса об общем виде линейного непрерывного функционала). Пусть H гильбертово пространство. Тогда для всякого непрерывного линейного функционала f на H существует единственный вектор 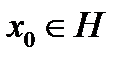 такой, что
такой, что 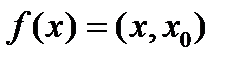
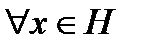 , причем
, причем 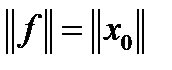 .
.
 Пусть вектор
Пусть вектор 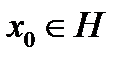 существует. Скалярное произведение линейно по первому аргументу, поэтому при любом
существует. Скалярное произведение линейно по первому аргументу, поэтому при любом 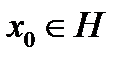 формула
формула 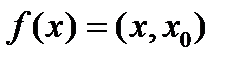 определяет линейный функционал на H. Из неравенства Буняковского
определяет линейный функционал на H. Из неравенства Буняковского 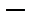 Коши следует, что
Коши следует, что 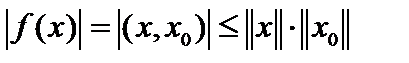 , то есть норма f не превосходит
, то есть норма f не превосходит 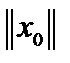 , а значит, функционал f непрерывен. Однако,
, а значит, функционал f непрерывен. Однако, 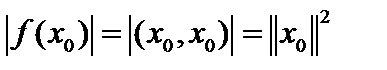 и, следовательно,
и, следовательно, 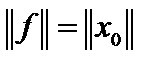 . Покажем теперь, что вектор
. Покажем теперь, что вектор 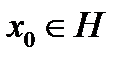 существует и единственен.
существует и единственен.  Существование.
Существование.  Поскольку функционал f непрерывен, то его ядро замкнуто и все пространство H представляется в виде:
Поскольку функционал f непрерывен, то его ядро замкнуто и все пространство H представляется в виде: 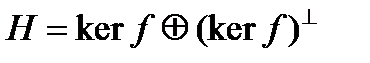 . Стало быть
. Стало быть 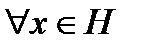 существует и единственно представление
существует и единственно представление 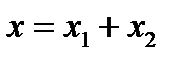 , где
, где 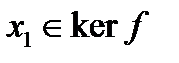 , а
, а  . Если
. Если 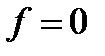 , то
, то 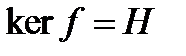 ,
, 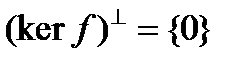 и, положив
и, положив 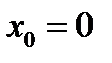 сразу получим
сразу получим 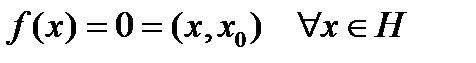 . Если
. Если 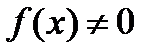 ,то
,то 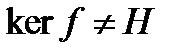 и ортогональное дополнение к ядру
и ортогональное дополнение к ядру 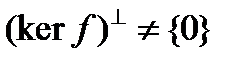 имеет размерность 1. Пусть вектор
имеет размерность 1. Пусть вектор 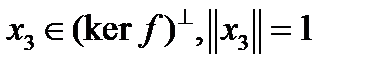 такой, что для любого вектора
такой, что для любого вектора  найдется число
найдется число 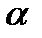 такое, что
такое, что 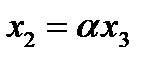 , а значит, для любого вектора
, а значит, для любого вектора 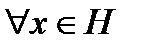 найдутся вектор
найдутся вектор 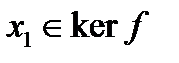 и число
и число 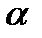 такие, что
такие, что 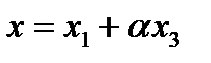 . Стало быть,
. Стало быть, 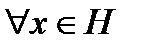 имеем
имеем 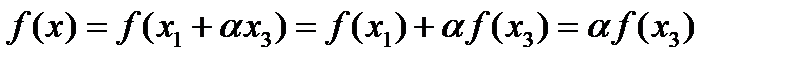 . Тогда, учитывая, что
. Тогда, учитывая, что 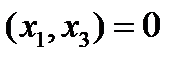 , а
, а 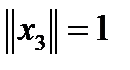 , получим
, получим 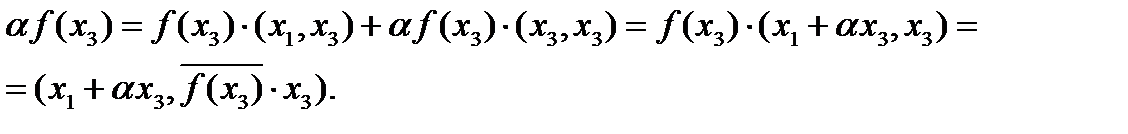 Обозначив
Обозначив 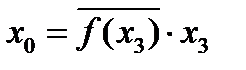 , сразу получим
, сразу получим 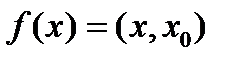 .
.  Единственность вектора
Единственность вектора 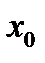 .
.  Допустим, что нашлось два вектора
Допустим, что нашлось два вектора 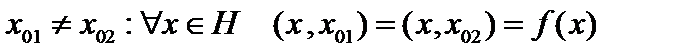 Тогда для всех
Тогда для всех 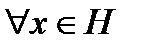 имеем
имеем 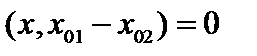 . Полагая в последнем равенстве
. Полагая в последнем равенстве 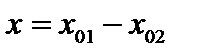 , получим
, получим 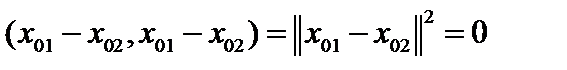 , а значит
, а значит 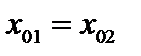 .
. 
Комментарий. Из теоремы Рисса следует, что правило, которое сопоставляет вектору 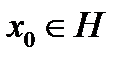 непрерывный линейный функционал f по формуле
непрерывный линейный функционал f по формуле 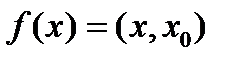 определяет линейный изоморфизм векторных пространств H и H*. Следовательно, H и H* ”с точностью до обозначений” являются одним и тем же пространством.
определяет линейный изоморфизм векторных пространств H и H*. Следовательно, H и H* ”с точностью до обозначений” являются одним и тем же пространством.
Сопряжённые операторы
Комментарий. Пусть 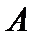
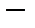 непрерывный линейный оператор, действующий в гильбертовом пространстве
непрерывный линейный оператор, действующий в гильбертовом пространстве 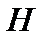 . Зафиксировав
. Зафиксировав 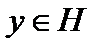 , рассмотрим скалярное произведение
, рассмотрим скалярное произведение 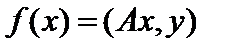 как функционал относительно переменной
как функционал относительно переменной 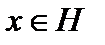 . Оператор
. Оператор 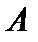 линеен, то есть функционал линеен по переменной
линеен, то есть функционал линеен по переменной 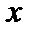 и ограничен, так как
и ограничен, так как 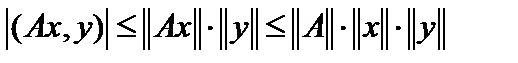 . По теореме Рисса о виде непрерывного линейного функционала, заданного на
. По теореме Рисса о виде непрерывного линейного функционала, заданного на 
 пространстве, имеет место равенство
пространстве, имеет место равенство 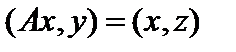 . Здесь элемент
. Здесь элемент 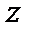 однозначно определен элементом
однозначно определен элементом 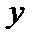 и оператором
и оператором 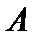 , то есть определяет некий оператор
, то есть определяет некий оператор 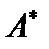 как
как 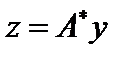 .
.
Определение 1. Оператор 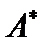 называют сопряженным к оператору
называют сопряженным к оператору 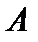 . Другими словами, оператор
. Другими словами, оператор 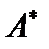 называется сопряжённым к
называется сопряжённым к 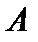 , если
, если 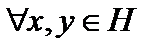 скалярное произведение
скалярное произведение 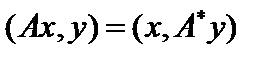 . Оператор
. Оператор 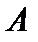 называется самосопряжённым, если
называется самосопряжённым, если 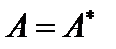 , унитарным, если
, унитарным, если 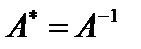 , и нормальным, если
, и нормальным, если 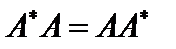 .
.
Рассмотрим сопряженноек гильбертову пространству  пространство
пространство 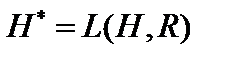 непрерывных линейных функционалов, заданных на гильбертовом пространстве
непрерывных линейных функционалов, заданных на гильбертовом пространстве 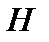 .
.
Определение 3. Последовательность 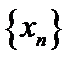 в гильбертовом пространстве
в гильбертовом пространстве 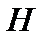 называется слабо сходящейсяк элементу
называется слабо сходящейсяк элементу 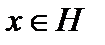 , если
, если  , то есть
, то есть 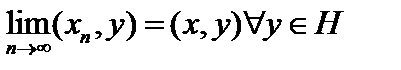 .
.
Комментарий. 1. Значение функционала 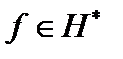 в точке
в точке 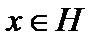 обозначается как скалярное произведение
обозначается как скалярное произведение 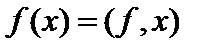 . Тогда сопряжённый оператор можно определить, как
. Тогда сопряжённый оператор можно определить, как 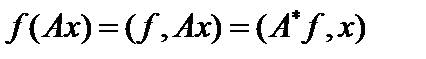 . Но это просто обозначение, маскирующее отсутствие в
. Но это просто обозначение, маскирующее отсутствие в 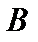 - пространствах скалярного произведения. Даже в конечномерном случае, когда
- пространствах скалярного произведения. Даже в конечномерном случае, когда 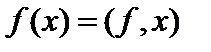 имеет смысл скалярного произведения, вектор
имеет смысл скалярного произведения, вектор 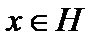 контравариантен, а вектор
контравариантен, а вектор 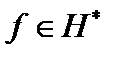 - это вектор коэффициентов преобразований, он ковариантен. Эти векторы находятся в разных пространствах и по-разному преобразуются при смене системы координат.
- это вектор коэффициентов преобразований, он ковариантен. Эти векторы находятся в разных пространствах и по-разному преобразуются при смене системы координат.
2.Напомним, что сходимость по норме пространства носителей  это обычная сходимость, когда
это обычная сходимость, когда 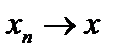 , то есть
, то есть 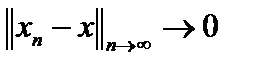 . Её называют сильной. Если носителем является пространство
. Её называют сильной. Если носителем является пространство 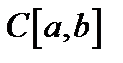 , то такая сходимость называется равномерной сходимостью. В пространстве непрерывных линейных операторов
, то такая сходимость называется равномерной сходимостью. В пространстве непрерывных линейных операторов 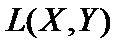 сходимость
сходимость 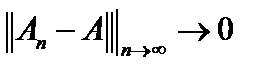 всегда называется равномерной сходимостью. Если же
всегда называется равномерной сходимостью. Если же 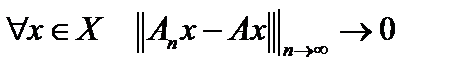 , то такая сходимость в пространстве
, то такая сходимость в пространстве 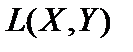 называется поточечной или сильной. Используя понятие сопряжённого пространства, в пространстве носителей можно ввести и другой тип сходимости, то есть другую топологию, а именно, слабую сходимость. Но это, по сути, поточечная сходимость. Сильная сходимость влечёт слабую, так как
называется поточечной или сильной. Используя понятие сопряжённого пространства, в пространстве носителей можно ввести и другой тип сходимости, то есть другую топологию, а именно, слабую сходимость. Но это, по сути, поточечная сходимость. Сильная сходимость влечёт слабую, так как 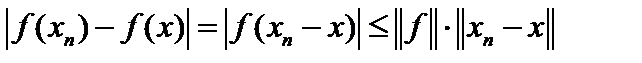 , и при
, и при 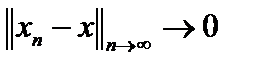 , то есть сильно,
, то есть сильно, 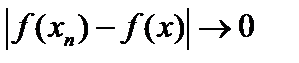 , то есть слабо. Обратное, вообще говоря, неверно. Пусть
, то есть слабо. Обратное, вообще говоря, неверно. Пусть 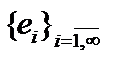 - базис в
- базис в 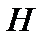 - пространстве и функционал
- пространстве и функционал 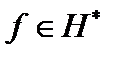 . Из теоремы Рисса об общем виде функционала в гильбертовом пространстве,
. Из теоремы Рисса об общем виде функционала в гильбертовом пространстве, 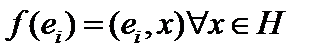 . Ясно, что последовательность
. Ясно, что последовательность 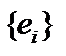 не стремится к нулю, она даже не фундаментальна, так как
не стремится к нулю, она даже не фундаментальна, так как 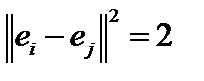 . Но по свойству коэффициентов Фурье последовательность
. Но по свойству коэффициентов Фурье последовательность 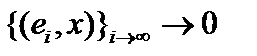 , то есть слабо.
, то есть слабо.
Пример 1. Рассмотрим оператор Фредгольма 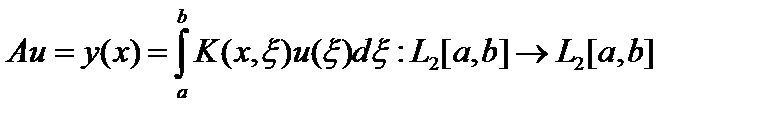 , где функция
, где функция 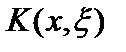 , то есть ядро оператора
, то есть ядро оператора 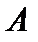 удовлетворяет условию Гильберта-Шмидта
удовлетворяет условию Гильберта-Шмидта 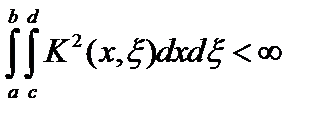 . Тогда
. Тогда 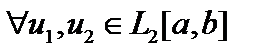
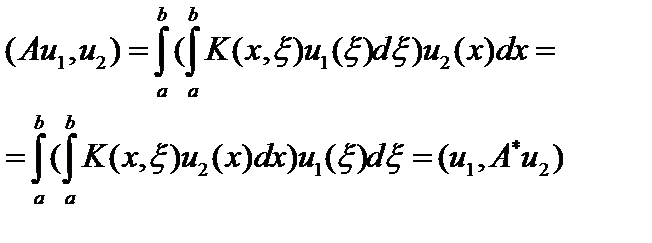 .
.
Но с другой стороны,
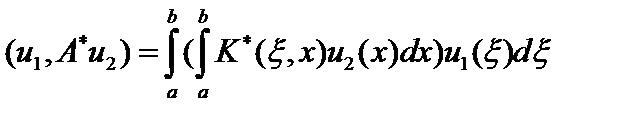 , то есть
, то есть 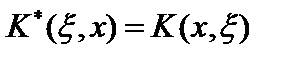 .
.
Итак, оператор 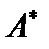 также является оператором Фредгольма с ядром
также является оператором Фредгольма с ядром 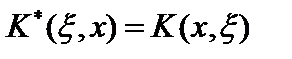
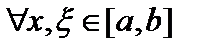 . Если
. Если 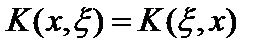
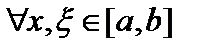 ,то ядро
,то ядро 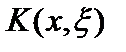 называется симметрическим. В этом случае, при
называется симметрическим. В этом случае, при 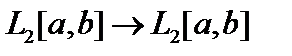 , интегральный оператор является самосопряженным. Если ядро интегрального оператора не симметрическое, то оператор не самосопряжён.
, интегральный оператор является самосопряженным. Если ядро интегрального оператора не симметрическое, то оператор не самосопряжён.
Пример 2. Рассмотрим в пространстве 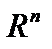 оператор
оператор 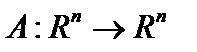 , то есть
, то есть 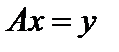 , причём
, причём 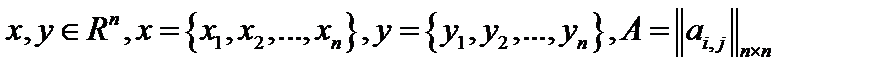 . По определению
. По определению 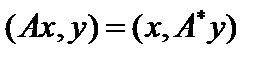 , то есть
, то есть 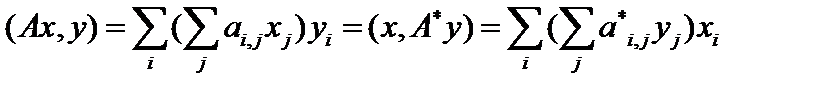 . Поменяв местами индексы, сразу получим, что
. Поменяв местами индексы, сразу получим, что 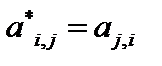 , то есть переход к сопряженному оператору в действительном
, то есть переход к сопряженному оператору в действительном 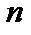 -мерном пространстве означает транспонирование матрицы этого оператора.
-мерном пространстве означает транспонирование матрицы этого оператора.
Пример 3. Показать, что если в гильбертовом пространстве H последовательность xn слабо сходится к x и 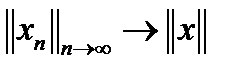 , то последовательность xn сходится сильно.
, то последовательность xn сходится сильно.

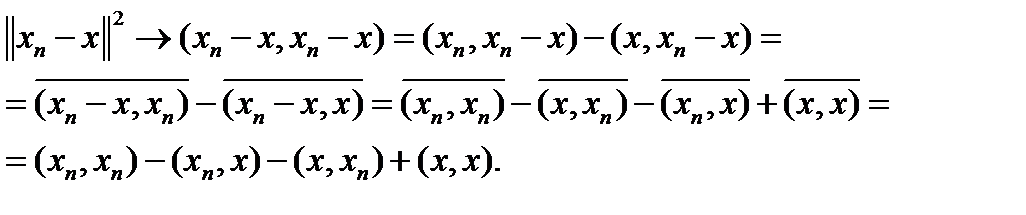
В силу непрерывности скалярного произведения 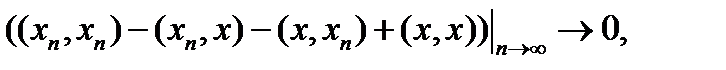 то есть
то есть 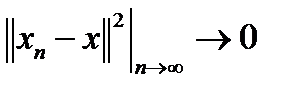 , что и означает сходимость по норме, то есть сильную сходимость.
, что и означает сходимость по норме, то есть сильную сходимость. 
