Теорема 1(признак возрастания и убывания функции)

Производная функции и ее геометрический смысл.

Приращением арг. ∆x наз.разность x-x₀,т.е. ∆x=x- x₀

Приращением функции y =f(x) в точке x₀ называется разность

Δу=f(x)-f(x₀)

Производной от функции y=f(x) в точке х0 наз. Предел отношения Δу/Δх, когда Δх→0 (при усл., что этот предел существует )lim Δу/Δх= f’(x0

Δх→0

обозначение производной.y’(x),f’(x)

Геометрический смысл производной.

Пусть Г- график функции y=f(x). Рассмотрим на Г т. А(x0,f(x0)) и т. В (x0+Δx,f(x0+Δx))

В

С

y=f(x) А

Прямая АВ называется секущей. Будем считать, что y=f(x)-непрерывная функция, тогда если Δх→0, то f(x0+Δx)→f(x0), т.е. В→А при Δх→0.

Пусть фи – угол наклона секущей относительно оси ОХ. Если существует предел lim γ=γ0 при Δх→0, то прямая, проходящая через А и образующая с осью ОХ угол γ0, называется касательной к Г в точке А.

Пусть С(f(x0+Δх), f(x0)) – точка, дополняющая отрезок АВ до прямоуг. треугольника АВС. Т.к. АС//ОХ, то tgγ =Δу/Δх. Переходя к пределу, получим: tgγ0=f′(x0)

Т.е. геометрический смысл производной состоит в том, что f′(x0) – это тангенс угла наклона касательной к графику y=f(x) в точке (x0,f(x₀))_.

2. Таблица производных, правила дифференцирования, производная сложной функции Таблица производных:

16-19 НЕ НАДО!

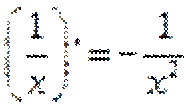Правила дифференцирования

Функция назыв.дифференцируемой в точке х_0,если она имеет производную в этой точке.

Теорема: Если f(x) и g(x) дифферен. в точке х, то: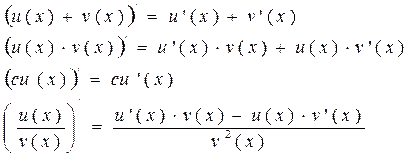

Производная сложной функции

Формула:

(u(v(x)))’=u’_v*v’_x

Дифференциал функции и его применение к приближенным вычислениям.

Дифференциал функции.

Определение: Дифференциалом функции называется главная часть ее приращения,линейная относительно приращения аргумента:

dy= f ′ (х) ∆х;

Дифференциалом аргумента х считается его приращение

dx=∆х;

Если приращение агрументаDх мало по абсолютной величине, то Dу приблизительно=dy,а для функции будет выполняться приближенное равенство:

f(x₊Dx)приблизительно= f(x)+ dy

Свойства дифференциала:стр.39

Производные и дифференциалы высших порядков.

Определение: Производная второго порядка называется производная производной данной функции:

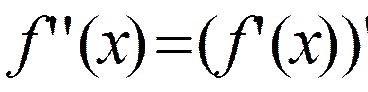
Определение:Производная n-го порядка называется производной производной n-1-го порядка.

d²y=y”dx² – диф-л 2-го порядка

dⁿy=d(d^n-1y)-дифферен.n-го порядка

Применение производной к вычислению пределов (правило Лопиталя).

Правила Лопиталя.

Если функция f(x), g(x) дефференцирована в окресности т. x₀, причем lim f(x)=lim g(x)=0 (g’(x) ≠0) или lim f(x)=lim g(x)=∞ при этом

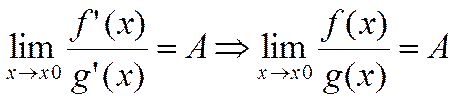
Возрастание и убывание функции (признак возрастания и убывания), критические точки и экстремумы функции. Необходимый и достаточный признак существования экстремума

Условия монотонности функции.

Функция у=f(x) наз.возрастающей(убывающей) на интервале (а, b) если для любых х₁ и х₂ из (а, b) таких что х₁<х₂ выполняется неравенство:

1)f(x₁)<f(x₂)-для возрастания

2) f(x₁)>f(x₂)-для убывания

Теорема 1(признак возрастания и убывания функции)

Если f’(x)>0 для любого x принадлежащего (а, b) то функция y=f(x) возрастает на (a,b);

Если f’(x)< 0 для любого x принадлежащего (а, b) то функция y=f(x) убывает на (a,b);

Промежутки возрастания и убывания функции наз.промежутками монотонности.

Определение.Точка х₀ назыв.точкой максимума(минимума) функции y=f(x) если существует такое полож.число ∆σ >0,что из неравенства │x-x0│<σследует неравенствo f(x₀)>f(x) (f(x₀)<f(x))

Определение 3.Значение функции в точке максимума (минимума) назыв.максимумом(минимумом) функции.

Точки максимума и минимума,назыв.точками экстремума,а максимумы и минимумы функции назыв.экстремумами функции.

Теорема 2(Необходимый признак существования экстремума)

Если функция у=f(x) имеет в точке х0 экстремум то производная f’(x0)=0 или не существует.

Определение 4.Точки,принадлежащие области определения ф-ции,производная в которых =0 или не существует назыв.критическими точками.

Теорема 3(достаточный признак экстремума)

1)Если при переходе через критическую точку производня меняет знак ,то в данной точке экстремум есть;если знак производной не меняется то в критической точке экстремума нет.

2)Если при переходе слева направо через критическую точку производная меняет знак с + на - ,то это точка максимума.Если с – на + то точка минимума

7.Асимптоты графика функции.

Асимптоты.

Опр. Асимптотой функции у=f(x) называется прямая к которой функция неограничена приближается при х стремящемся к бесконечности.

Опр. Прямая х=х₀ назыв.вертикальной асимптотой графика функции у=f(x) если хотя бы один из односторонних пределов f(x₀-0) или f(x₀+0) = бесконечности.

Опред.Прямая y=kx+b назыв.наклонной асимптотой графика функции f(x) при х стремящемся к +- бесконечности если функция f(x) может быть представлена в виде f(x)= kx+b+альфа(х), где альфа(х) стремится к 0.

Для нахождения k и b используются формулы::

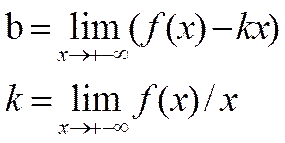
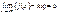8.Выпуклость и вогнутость графика функции, точки перегиба.