Метод елементарних перетворень

ЗМ 3 Ранг матриці. Обернена матриця

Ранг матриці

Мінори певного порядку можна визначити для будь-якої (не лише квадратної )матриці. Матриця може мати багато мінорів, причому деякі з них можуть дорівнювати нулю, а інші – ні.

Рангом матриці називається найбільший порядок відмінного від нуля мінора матриці. Ранг нульової матриці дорівнює нулю.

Ранг матриці 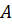позначається таким чином: , , , .

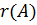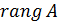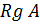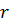Для визначення рангу матриці використовують:

v метод обвідних мінорів;

v метод елементарних перетворень.

Метод обвідних мінорів

1. Знаходимо який-небудь мінор 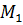першого порядку (тобто елементи матриці) відмінний від нуля. Якщо такого мінора не має, то 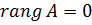(матриця нульова.

2. Обчислюємо мінори другого порядку, які місять в собі 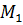(обводять 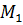) до тих пір, поки не знайдеться мінор 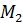відмінний від нуля. Якщо такого мінора не має, то 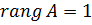, якщо є, то 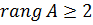. І т.д.

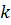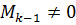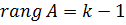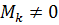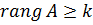3. Обчислюємо мінори -го порядку, якщо вони існують, які обводять мінор . Якщо таких мінорів не має, або вони всі дорівнюють нулю, то , якщо хоча б один мінор , то і т.д.

При знаходженні рангу матриці таким способом достатньо на кожному кроці знайти всього один ненульовий мінор 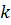-го порядку, причому шукати його потрібно тільки серед мінорів, які обводять мінор .

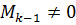Метод елементарних перетворень

В подальшому будемо розглядати елементарні перетворення тільки над рядками.

Справедливі наступні теореми.

Теорема 1.Елементарні перетворення не змінюють рангу матриці.

Теорема 2.Ранг ступінчастої матриці дорівнює кількості її ненульових рядків.

Ненульовий рядок – це рядок, який містить в собі хоча б один елемент, який не дорівнює нулю.

Рангу матриці дорівнює рангу ступінчастої матриці, яка одержана із даної матриці за допомогою елементарних перетворень.

Метод елементарних перетворень знаходження рангу матриці полягає в наступному:

1) матрицю 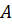за допомогою елементарних перетворень приводимо до ступінчастого виду;

2) підрахуємо число ненульових рядків одержаної матриці, це і буде рангом даної матриці .

Приклад. Знайти ранг матриці методом обвідних мінорів.

.

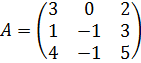Розв’язання.

Нагадуємо, що при обчисленні рангу матриці потрібно перейти від мінорів менших порядків до мінорів вищих порядків. Якщо вже знайдено мінор 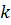-го порядку, який не дорівнює нулю, то далі потрібно обчислювати лише мінори 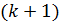-го порядку, що обводять цей мінор. Якщо всі вони дорівнюють нулю, то ранг матриці дорівнює .

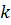Вибираємо, наприклад, мінор першого порядку 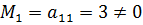. Розглянемо мінор другого порядку, що обводить мінор :

.

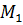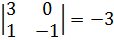Тепер переходимо до обчислення мінорів 3-го порядку, які обводять мінор 2-го порядку:

.

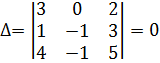Мінор 3-го порядку дорівнює нулю. Отже .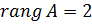

Відповідь. .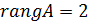

Приклад. Знайти ранг матриці за допомогою елементарних перетворень:

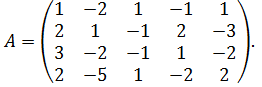
Розв’язання.

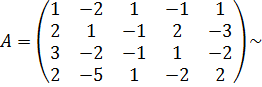
{елементи першого рядка помножимо на 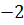і додамо до елементів другого та четвертого рядка}

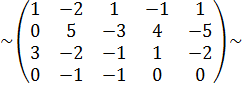
{елементи першого рядка помножимо на 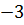і додамо до елементів третього рядка}

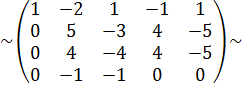
{поміняємо місцями елементи другого та четвертого рядків }

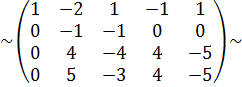
{елементи другого рядка помножимо на 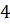і додамо до елементів третього рядка}

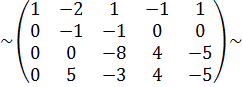
{елементи другого рядка помножимо на 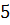і додамо до елементів четвертого рядка}

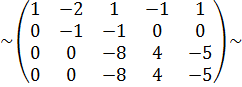
{елементи третього рядка помножимо на 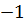і додамо до елементів четвертого рядка}

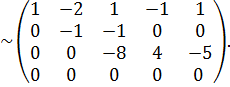
Одержали ступінчасту матрицю,яка має три ненульових рядка. Тому ранг цієї матриці, а тому і ранг матриці 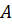дорівнює : .

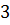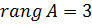Відповідь. .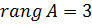

Обернена матриця

Очевидно, що ранг матриці не може перевищувати її порядок.

Ранги транспонованих матриць співпадають.

Матриця, ранг якої менший за її порядок, називається виродженою матрицею (матриця, визначник якої дорівнює нулю).

Для невироджених матриць (а такими можуть бути лише квадратні) вводять поняття оберненої матриці.

Матриця 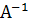називається оберненою до матриці 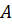, якщо справджуються рівності

.

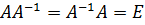Теорема. Кожна неособлива матриця має обернену, і до того ж тільки одну.

Матрицю 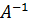, яка є оберненою до матриці 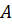, знаходять за формулою

,

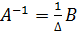Де 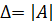, а 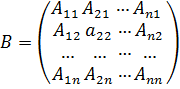- матриця, що складена з алгебраїчних доповнень 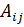до елементів 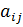матриці 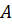і транспонована; матриця 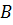називається приєднаною матрицею до матриці .

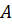Властивості обернених матриць

1.

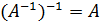
2.

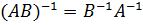
3.

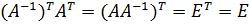
4.

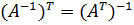
5.

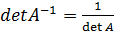
Приклад.Знайти матрицю, обернену заданій матриці A:

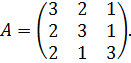
Розв’язання:

1. Обчислюємо визначник матриці:

.

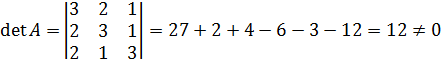Матриця A не вироджена, тому проводимо обчислення далі

2. Знайдемо алгебраїчні доповнення до елементів матриці A.

;

;

;

;

;

;

;

;

.

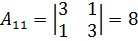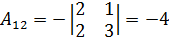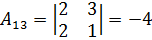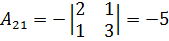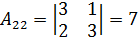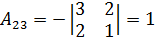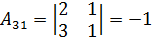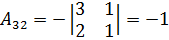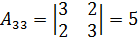3. Запишемо матрицю 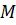, складену з алгебраїчних доповнень елементів матриці :

.

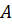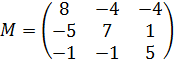4. Транспонуємо матрицю :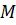

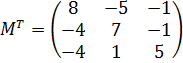
5. Запишемо обернену матрицю :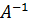

.

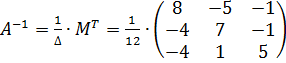Зауваження. Матрицю 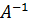можна залишити в такому вигляді, а можна кожний елемент матриці помножити на число :

.
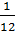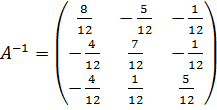Необхідно перевірити правильність виконання операцій, тобто перевірити, що 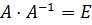.