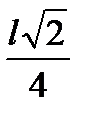Рассмотрим примеры определения перемещений в СОС от действующей нагрузки. Во всех случаях изгибная жесткость элементов системы – EJ и их продольная жесткость – EF предполагаются известными.
Пример 3.1. Определить максимальные прогибы балки (рис. 3.14, а).
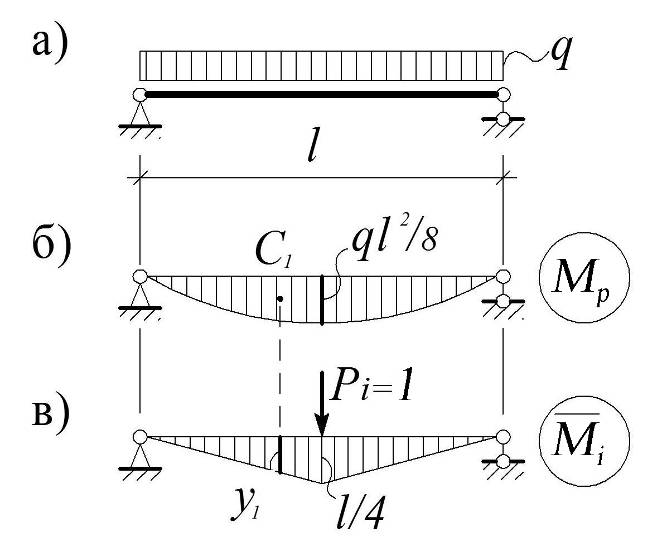
Рис. 3.14
Решение. В соответствии с формулой (3.17) строим эпюру Mp от заданной нагрузки (рис. 3.14, б) и эпюру `Mi от единичной силы, приложенной в середине балки (рис. 3.14, в).
Вычислим интеграл (3.17) по формуле Верещагина. На всем промежутке [0,l] эпюра Mp является однозначной, то есть отвечает предъявляемым к ней требованиям, а эпюра`Mi на всем промежутке [0,l] будет нелинейной. Поэтому область интегрирования делим на два участка: [0, l/2] и [l/2, l], на каждом из которых `Mi(x) будет линейной. С учетом симметрии получим:
vmax = Dip = 2 (w1× yc1)/EJ = 2 [(2/3)×( l/2)×(ql2/8)]×[(5/8)×(l/4)] = 5ql4/384EJ. ·
Для того чтобы получить тот же результат с помощью интегрирования дифференциального уравнения изогнутой оси балки нужно затратить примерно втрое больше усилий – хотя бы потому, что придется находить угол поворота балки в ее начальном сечении – q0.
Формально воспользовавшись для всего промежутка [0,l] формулой Симпсона (3.21) и учитывая, что значения Mp и`Mi на его концах равны нулю, получим:
vmax = (l/6EJ)×4(ql2/8)×(l/4) = ql4/48EJ.
Найденный результат оказался неверным, поскольку на всем промежутке [0,l] подынтегральная функция f(x) = Mp(x) × `Mi (x) не отвечает требованиям, предъявляемым к ней этой формулой.
Пример 3.2. Найти линейное и угловое перемещения точки A на конце Г-образной консольной рамы, у которой жесткость стойки вдвое больше жесткости ригеля (рис. 3.15, а).
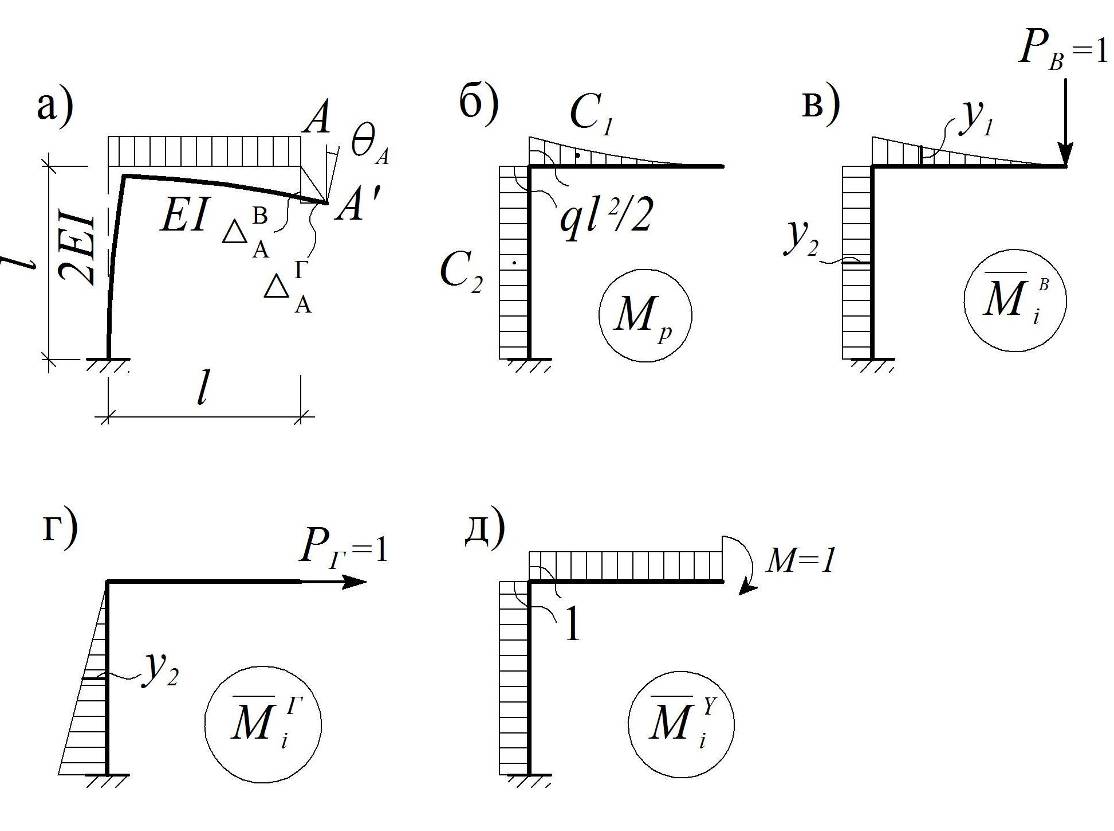
Рис. 3.15
Решение. Строим эпюру Mp от заданной нагрузки и эпюры`Mi от единичных сил и моментов, приложенных в точке A (рис. 3.15, б–д).
Определяем вертикальное перемещение точки А, перемножая эпюры Mp и`M в:
Dв = (Mp ´`M в) = (1/EJ) w1× y1 + (1/2EJ) w2× y2 = (1/EJ)[(1/3)×l×(ql2/2)]×(3/4)l +
+ (1/2EJ) [l×(ql2/2)]×l = (3/8)(ql4/EJ).
Находим горизонтальное перемещение точки А:
Dг = (Mp ´`M г) = (1/2EJ) [l×(ql2/2)]×(l/2) = (1/8)(ql4/EJ).
Полное перемещение точки А составит:
___________ __
DА = Ö (Dв)2 + (Dг)2 = (Ö10 ql4)/8EJ.
Угол поворота сечения в точке А будет равен:
qА = (Mp ´`M у) = (1/EJ) w1×1 + + (1/2EJ) w2×1 = (1/EJ)[(1/3)×l×(ql2/2)]×1 +
+ (1/2EJ) [l×(ql2/2)]×1 = (5ql3/12EJ ). ·
Рассмотренный пример наглядно показывает, почему при определении перемещений в рамах мы пренебрегаем продольными деформациями: вертикальное перемещение точки А от заданной нагрузки в основном определяется изгибом ригеля, изгибом стойки и только в очень незначительной степени – ее сжатием.
Пример 3.3. Найти угол поворота сечения на правой опоре рамы, рассмотренной в примере 2.5, полагая EJ = const (рис. 2.9, а).
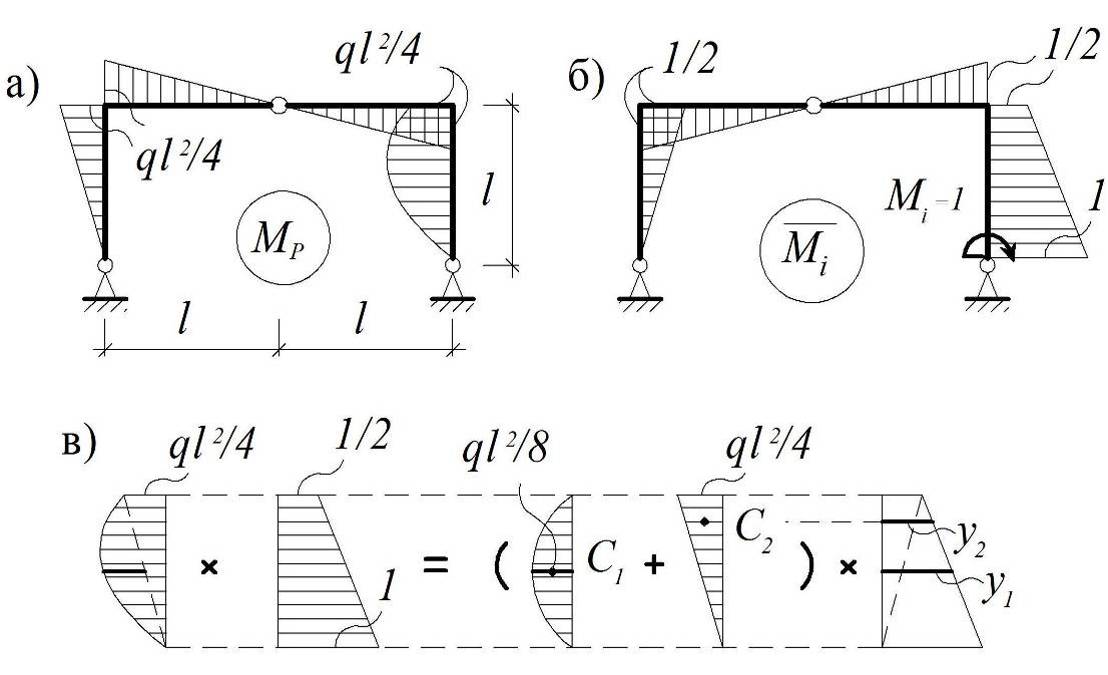
Рис. 3.16
Решение. Воспользуемся уже построенной ранее эпюрой Mp от заданной нагрузки (рис. 2.9, б) и (рис. 3.16, а), и умножим ее на эпюру`Mi от единичного момента (рис. 3.16, б). На левой стойке и ригеле эпюра Mp представлена тремя треугольниками с равной площадью wтр = (1/2) × l ×(ql2/4), которые умножаются на три одинаковых треугольника в эпюре `Mi.
Нестандартную эпюру Mp на правой стойке с площадью wпар представим суммой стандартных эпюр: параболы с площадью w1 и треугольника с площадью w2 (рис. 3.16, в).
Поскольку перемножаемые эпюры расположены на разных волокнах, результат получится со знаком минус. Как и при определении опорных реакций это означает, что действительное направление угла поворота будет противоположно направлению, указанному на рисунке:
qВ = (Mp ´ Mi) = (1/EJ) [(–3) wтр× yтр – wпар× yпар] = – (1/EJ) [3wтр × yтр+w1 × y1+
+w2 × y2] = – (1/EJ) {3 [(1/2) × l ×(ql2/4) ] × [(2/3)×(1/2)] + [(2/3) × l ×(ql2/8)] ×
× [(1/2)(1/2+1)] + [(1/2) l (ql2/4) ] × [(2/3)(1/2) + (1/3) × 1]} = – (11ql3) / (48EJ). ·
Пример 3.4. Полагая EJ = const, найти взаимное сближение точек i и j рамы, взаимный угол поворота соответствующих сечений, а также построить деформированную схему рамы от заданной нагрузки (рис. 3.17, а).
Решение. Взаимное сближение точек i и j можно найти с помощью стандартной процедуры определения перемещений.
Для этого нужно построить эпюру MP от заданной нагрузки (рис. 3.17, б), а также эпюры`Mi и`Mj от единичных сил, приложенных в этих точках в направлении ij (рис. 3.17, в-г), и определить перемещения Δi и Δj соответственно. Искомое взаимное сближение точек i и j будет равно Δij = Δi – Δj.
Однако легче получить тот же результат, умножив эпюру MP на эпюру `MijΔ от единичных сил, приложенных в этих точках и направленных навстречу друг другу, поскольку эпюра`MijΔ от взаимно уравновешенной нагрузки будет проще каждой из эпюр`Mi и`Mj (рис. 3.17, д).
Аналогичным образом поступим и при определении взаимного угла поворота сечений θij, умножив эпюру MP на эпюру`Mijθ от единичных моментов, приложенных в точках i и j и направленных навстречу друг другу (рис. 3.17, е).
Таким образом, получим:
Δij = (MP ´`MijΔ) = – (1/EJ) [ (1/2) ×(l/2)×(Pl/4)] × [(1/3) × ( 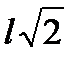 )/4] =
)/4] =
= – (1/EJ) ×(Pl2/16) × ( 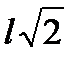 )/12 = – (1/EJ) ×(Pl3
)/12 = – (1/EJ) ×(Pl3 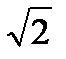 )/192;
)/192;
θij = (MP ´`Mijθ) = (1/EJ) × ((1/2) ×(l/2)×(Pl/4)) × 1 = (1/EJ) × (Pl2/16).
Переходя к построению деформированной схемы рамы, отметим два обстоятельства.
Во-первых, эпюра моментов располагается на растянутых волокнах рамы, поэтому стойки рамы, на которых моменты равны нулю, остаются недеформированными.
Рис. 3.17
Во-вторых, углы, которые образуют между собой стержни рамы, соединенные в жестких узлах, не меняются при ее деформации. В этом нетрудно убедиться, если определить взаимный угол поворота сечений, проходящих через точки k и l, у левого верхнего узла рамы (рис. 3.17, ж). Когда точки k и l приближаются к этому узлу, площадь соответствующей эпюры`Mklθ будет стремиться к нулю, поэтому θkl = (MР ´`Mklθ) также устремится к нулю.
Таким образом, для построения деформированной схемы рамы достаточно определить горизонтальное и вертикальное перемещения точки j, либо линейное ΔiP и угловое θiP перемещения сечения у опоры B (рис. 3.17, з). ·



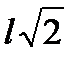 )/4] =
)/4] =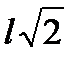 )/12 = – (1/EJ) ×(Pl3
)/12 = – (1/EJ) ×(Pl3 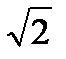 )/192;
)/192;