Типа с клиновым креплением крышки
- для нижней поперечины и крышки станины по формулам (7.13)-(7.17)
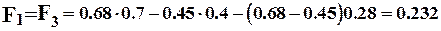 м2,
м2,
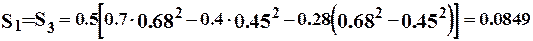 м3,
м3,
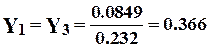 м,
м,
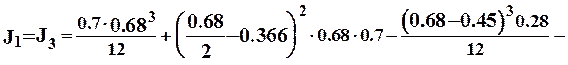
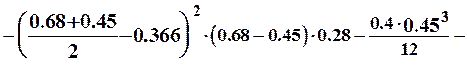
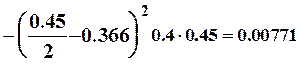 м4.
м4.
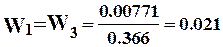 м3.
м3.
Длина нейтральной линии поперечины и стойки по формулам (7.25) и (7.44) соответственно
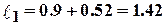 м,
м, 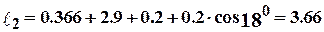 м.
м.
Расстояние от точки приложения силы Т до выступа станины (см. рис. 7.11 и 7.12)
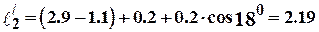 м.
м.
Расстояние от нейтральной линии стойки до точки приложения силы 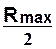 в клиновом креплении (см. рис. 7.11)
в клиновом креплении (см. рис. 7.11) 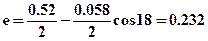 м и расстоянии от нейтральной линии стойки до середины выступа
м и расстоянии от нейтральной линии стойки до середины выступа 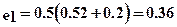 м.
м.
Рассмотрим условия прокатки в верхнем горизонте (между средним и верхним валками)
Силу защемления подушки определим по формуле (7.43), подставляя вместо  длину
длину 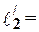 2.19 м и вместо
2.19 м и вместо  расстояние
расстояние 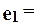 0.36 м.
0.36 м.
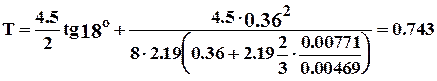 МН.
МН.
Рассчитываем изгибающие моменты в опасных сечениях:
- стойки по формуле (7.51) при
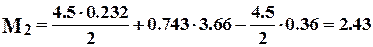 МН×м;
МН×м;
- крышки по формуле по формуле (7.50)
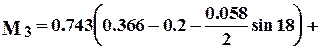
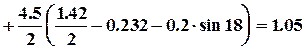 МН×м.
МН×м.
Рассчитываем напряжения в опасных сечениях станины по формулам (7.46) и (7.47):
- в стойках 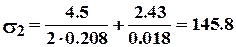 МПа;
МПа;
- в крышке 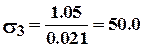 МПа.
МПа.
Коэффициенты запаса прочности при 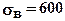 МПа будут равны:
МПа будут равны:
- в стойке 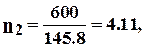 ,
,
- в крышке 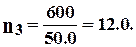 .
.
Полученные результаты позволяют сделать вывод, что для крышки станины условие прочности (1.2) выполняется, а стойки станины в сечении у основания коэффициент запаса прочности меньше допустимого  Следовательно имеется вероятность поломки станины по этому сечению.
Следовательно имеется вероятность поломки станины по этому сечению.
Для выступа стойки рассчитаем напряжения среза по формуле (7.41)
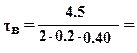 28.1 МПа,
28.1 МПа,
и напряжения изгиба по формуле(7.42)
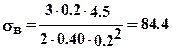 МПа.
МПа.
Рассчитываем коэффициенты запаса прочности :
по нормальным напряжениям 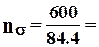 7.1,
7.1,
по касательным напряжениям при 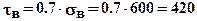 МПа
МПа
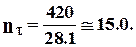
Таким образом выступы станины также имеют пониженную прочность по нормальным напряжениям.
Рассмотрим прочностные условия в станине при прокатке в нижнем горизонте (между нижним и средним валками).
Определим реактивную силу, действующую на стойку при защемлении крышки, по формуле (7.43)
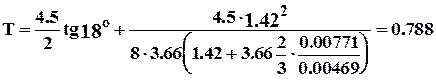 МН.
МН.
Рассчитаем изгибающие моменты в опасных сечениях нижней поперечины и стойки по формулам (7.48) и (7.49): :
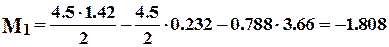 МН×м;
МН×м;
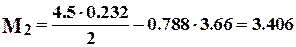 МН×м;
МН×м;
Напряжения в опасных сечениях поперечины и стойки найдем по формулам (7.45) и (7.46):
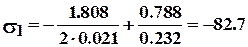 МПа;
МПа;
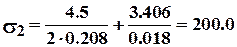 МПа;
МПа;
Соответственно этим напряжениям коэффициенты запаса составят
- в поперечине 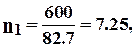
- в стойке 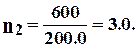
Таким образом как в стойке, так и в поперечине коэффициенты запаса прочности получились ниже допустимых  Наиболее слабым местом является сечение стойки у нижнего основания. В этом месте имеется вероятность поломки станины. Поэтому эксплуатация рассматриваемой рабочей клети при указанном усилии на шейки валков нецелесообразна.
Наиболее слабым местом является сечение стойки у нижнего основания. В этом месте имеется вероятность поломки станины. Поэтому эксплуатация рассматриваемой рабочей клети при указанном усилии на шейки валков нецелесообразна.
ЖЕСТКОСТЬ РАБОЧИХ КЛЕТЕЙ
Жесткость рабочих клетей - один из важнейших факторов, определяющих точность размеров проката. Количественно жесткость клети оценивают коэффициентом (модулем) жесткости, равным
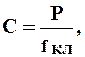
 (8.1)
(8.1)
где Р - полное усилие прокатки; 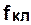 - общая упругая деформация всех элементов рабочей клети по действием усилия Р. Коэффициент жесткости определяет величину усилия прокатки, при котором установочный зазор между валками увеличивается за счет упругой деформации клети на 1 мм.
- общая упругая деформация всех элементов рабочей клети по действием усилия Р. Коэффициент жесткости определяет величину усилия прокатки, при котором установочный зазор между валками увеличивается за счет упругой деформации клети на 1 мм.
Коэффициенты жесткости рабочих клетей современных прокатных станов изменяются в следующих пределах, кН/мм [1-4]:
проволочные 400 - 700,
мелкосортные 600 - 1000,
среднесортные 700 - 1300,
крупносортные 800 - 1600,
толстолистовые 4000-7000,
тонколистовые горячей прокатки 4500-8000,
тонколистовые холодной прокатки 5500-10000.
Для теоретического определения коэффициента жесткости клети необходимо при известном усилии прокатки рассчитать ее общую упругую деформацию, которая равна сумме упругих деформаций всех ее деталей:
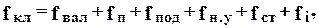 (8.2)
(8.2)
где 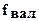 ,
, 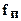 ,
, 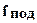 ,
, 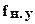 ,
, 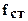 ,
, 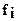 - упругая деформация соответственно валков, подушек, подшипников, деталей нажимного устройства, станины и других элементов (стакана, клиньев, подкладок и т.п.). Методы расчета указанных составляющих упругой деформации клети изложены в работах [1-4,7,8]
- упругая деформация соответственно валков, подушек, подшипников, деталей нажимного устройства, станины и других элементов (стакана, клиньев, подкладок и т.п.). Методы расчета указанных составляющих упругой деформации клети изложены в работах [1-4,7,8]
Упругая деформация валков
8.1.1. Деформация валков листовых станов. Основной деформацией рабочих валков двухвалковых клетей является их прогиб под действием распределенной по длине бочки нагрузки со стороны полосы. В клетях кварто основная деформация валкового узла определяется прогибом опорных валков, поскольку практически все усилие прокатки передается на опорные валки, а прогиб рабочих валков лимитируется прогибом опорных валков. Кроме того, при холодной прокатке возникают упругие деформации сплющивания на контакте рабочего валка с опорным, а также рабочего валка с полосой.
Таким образом, в общем виде, деформация валковой системы определяется выражением
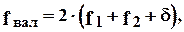 (8.3)
(8.3)
где 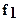 - прогиб валка под действием изгибающих моментов;
- прогиб валка под действием изгибающих моментов; 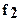 - прогиб валка в результате действия поперечных сил; d- радиальное сплющивание валка.
- прогиб валка в результате действия поперечных сил; d- радиальное сплющивание валка.
Максимальный прогиб валка листового стана под действием усилия прокатки Р будет иметь место по середине бочки. Слагаемые 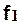 и
и 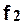 в формуле (8.3) рассчитывают по формулам (см. рис. 2.1):
в формуле (8.3) рассчитывают по формулам (см. рис. 2.1):
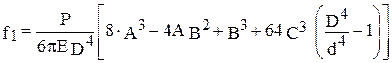 , (8.4)
, (8.4)
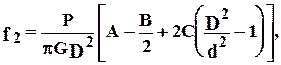 (8.5)
(8.5)
где С - расстояние от края бочки валка до точки приложения усилия на шейку валка; В - ширина прокатываемого листа; D и d - соответственно диаметр бочки и шейки валка; Е и G - соответственно модуль упругости и модуль сдвига материала валка. Ориентировочно можно принимать 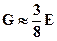 .
.
Сплющивание валковопределяют по формуле:
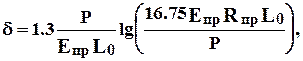 (8.6)
(8.6)
где L0 - длина участка сплющивания, которую обычно принимают на контакте опорного и рабочего валков равной длине бочки валков L, а на контакте рабочего валка и полосы - ширине прокатываемого листа В; 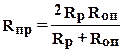 - приведенный радиус валков, опорного (оп) и рабочего (р);
- приведенный радиус валков, опорного (оп) и рабочего (р); 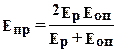 - приведенный модуль упругости материала валков. Поскольку радиусы опорного Rоп и рабочегоRр валков значительно больше толщины прокатываемой полосы, сплющиванием на контакте полосы и рабочего валков можно пренебречь. При определении величины d для станов дуо принимают
- приведенный модуль упругости материала валков. Поскольку радиусы опорного Rоп и рабочегоRр валков значительно больше толщины прокатываемой полосы, сплющиванием на контакте полосы и рабочего валков можно пренебречь. При определении величины d для станов дуо принимают 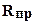 , равным радиусу валка, а
, равным радиусу валка, а 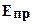 - модулю упругости материала валка.
- модулю упругости материала валка.
Прогиб листового валка по середине и на краю бочки неодинаков. Разность прогибов валка в середине бочки и у края прокатываемого листа Df  определяют по формуле
определяют по формуле
Df 
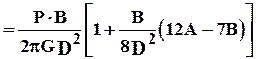 .
.
Для компенсации прогиба валка, его бочке придают выпуклость таким образом, чтобы эта выпуклость на ширине листа компенсировала указанную выше разность прогибов.
8.1.2. Деформация валков сортовых станов. Деформация рабочих валков сортовых станов определяется их прогибом под действием сосредоточенной силы ( или нескольких сил при одновременной прокатке в клети нескольких полос), сплющивание валков не учитывают. Поэтому деформация валкового узла сортового стана равна
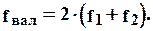 (8.7)
(8.7)
Величина прогиба сортового валка зависит от места расположения калибра, в котором ведется прокатка, т.е. от места приложения силы Р (см. рис. 2.4). При прокатке в одну нитку в калибре, расположенном на расстоянии Х от середины опоры, обе составляющие прогиба рассчитывают по формулам [7]:
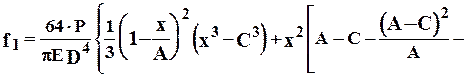
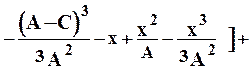
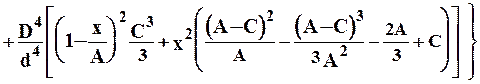 , (8.8)
, (8.8)
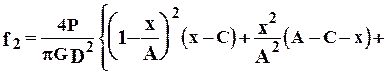
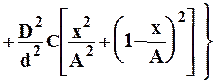 , (8.9)
, (8.9)
где D - диаметр валка по дну калибра.
Если прокатка ведется в калибре, расположенном по середине бочки валка при 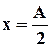 , то величину прогиба можно рассчитать по формулам (8.4) и (8.5), приняв В=0.
, то величину прогиба можно рассчитать по формулам (8.4) и (8.5), приняв В=0.
В случае многониточной прокатки для определения упругой деформации валков рекомендуется пользоваться методом, изложенным в работе [13].
Упругий прогиб консольно распложенного валка (см. рис. 2.6) можно рассчитать по формуле
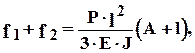 (8.10)
(8.10)
где 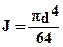 - момент инерции сечения приводного вала диаметром d.
- момент инерции сечения приводного вала диаметром d.
