Поставка с постоянной интенсивностью

Характерна для завод­ского склада, когда продукция производится партиями и с момента запуска ее в производство поступает на склад с постоянной ин­тенсивностью m >l (если m < l, то система не работает). Запуск производства вызывает фиксированные затраты c₀ на переналадку оборудования, которые не зависят от объема партии.

График изменения текущего объема запаса изображен на рис. 3.7.

Период времени между поставками содержит четыре ин­тервала:

[0, t₁] – интервал накопления запасов с интенсивностью (m –l), максимальный уровень запаса у₂ будет накоплен за время t₁, то есть

;

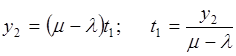[t₁, t₂] – интервал расходования запаса с интенсивностью l, весь запас будет израсходован к моменту времени t₂, то есть

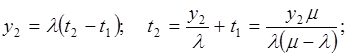(3.13)

[t₂, t₃] – интервал накопления дефицита, за время (t₃–t₃) будет накоплен максимальный дефицит

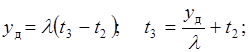(3.14)

[tз, Т₂] —интервал ликвидации дефицита с интенсивностью (m –l), дефицит будет ликвидирован за время T₂ – t₃, то есть

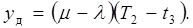
Подставляя в это уравнение t₃ из выражения (3.14) и t₂ из фор­мулы (3.13), находим

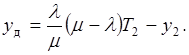
Затраты на хранение запасов в течение периода имеют место на интервале [0, t₂] и пропорциональны площади треугольника 0AВ, то есть

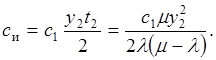
На интервале [t₂, Т₂]склад выплачивает штраф, размер кото­рого пропорционален площади треугольника BCD, то есть

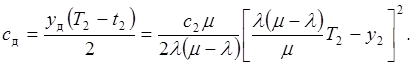
Функция затрат в единицу времени

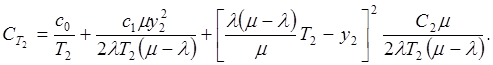
Приравнивая производные этой функции по у₂ и Т₂. нулю и ре­шая полученную систему уравнений, находим

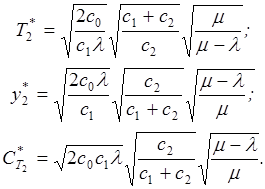(3.15)

Если возникновение дефицита не допускается (рис. 5.8), то

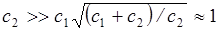и параметры Стратегии управления за­пасами

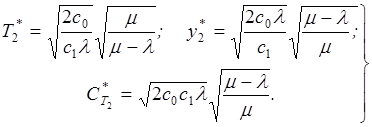(3.16)

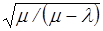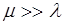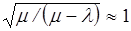Сравнивая выражения (3.15) с (3.9) – (3.11) и (3.16) с (3.5) – (3.6), можно установить, что при поставке с постоянной интенсивностью максимальный объем запаса, минимальное значение функции затрат и частота заказов уменьшаются в раз. Если , то и из формул (3.15) получаем выражения (3.9) – (3.11), а из (3.16) – (3.5) и (3.6).

Рассмотренные модели управления запасами могут использо­ваться для определения ориентировочных значений параметров стратегии управления запасами при вероятностном спросе.

3.3. ОДНОКАСКАДНЫЕ СУЗ ПРИ ВЕРОЯТНОСТНОМ
ДИСКРЕТНОМ СПРОСЕ

Главной особенностью управления запасами при вероятностном спросе является то, что теоретически исключить дефицит невоз­можно, а можно только обеспечить требуемое значение вероят­ности возникновения дефицита. Поэтому прежде всего рассмотрим методику определения этого показателя для однокаскадной систе­мы управления многономенклатурными запасами при следующих предположениях:

– дискретный вероятностный стационарный спрос представ­ляет простейший поток требований на предметы запаса интенсив­ности 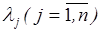, п – число номенклатур;

– стратегия управления запасами типа (Т, у_j) – периодиче­ская с пополнением объема запаса по каждой номенклатуре до максимального уровня у_j; пополнение запаса по всем номенкла­турам осуществляется одновременно;

– поставка осуществляется мгновенно, а ликвидация дефици­та – накоплением требований до очередной поставки.

Эффективность управления запасами по каждой номенклатуре будем характеризовать вероятностью возникновения дефицита q(у_j) или вероятностью его отсутствия 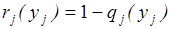в течение периода между поставками.

Дефицит по j-й номенклатуре в течение периода между по­ставками отсутствует, если число требований k на предметы запаса данной номенклатуры за период Т не превысит величины у_j, то есть 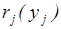– вероятность того, что за время Т в СУЗ поступит не бо­лее y_j требований.

Так как спрос представляет простейший поток требований, то вероятность Р_jk того, что за время Т в систему поступит ровно k требований на предметы запаса j-й номенклатуры, определяется по формуле Пуассона, то есть

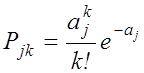, (3.17)

где 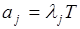– среднее ожидаемое число требований на предме­ты запаса за время Т. Для нестационарного пуассоновского потока

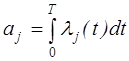
Дефицит отсутствует при k = 0, 1,2,. . ., у_j, то есть

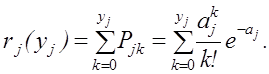(3.19)

Эффективность СУЗ в целом можно оценить вероятностью до­статочности объема запасов Y = (y₁, у₂, . . ., y_n) на период Т, кото­рая представляет собой вероятность отсутствия дефицита по всем номенклатурам

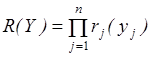, (3.20)

или вероятностью возникновения дефицита хотя бы по одной но­менклатуре

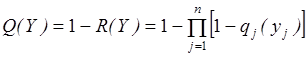. (3.20)

Выполнив умножение в выражении (3.20) и пренебрегая члена­ми, содержащими произведение двух и более величин q_j(y_j) находим

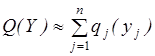(3.21)

Абсолютная погрешность вычисления Q(Y) по формуле (3.21) не превышает 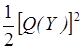и поэтому ее можно использовать при 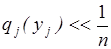При определении оптимальных параметров стратегии управле­ния запасами необходимо учитывать и такие характеристики СУЗ, как общая стоимость запасов C(Y), их вес G(Y), требуемая ем­кость склада V(Y):

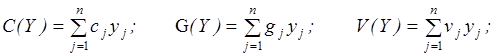(3.22)

где c_j – стоимость; G_j – вес предмета запаса j-й номенклатуры; V_j – требуемая емкость склада (объем или площадь) для его хра­нения.

Полученные зависимости (3.19), (3.21) и (3.22) позволяют сформулировать ряд задач оптимизации объема запасов Y для за­данного периода пополнения Т.

Задача 1. Определить объем запасов 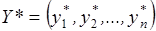так, чтобы их стоимость была минимальной то есть

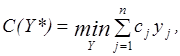(3.23)

а вероятность его достаточности R(Y) была не ниже заданной R_д, то есть

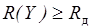, или 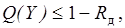(3.24)

и выполнялись ограничения по суммарному весу запасов и требуемой емкости склада

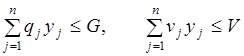, (3.25)

где G — допустимый вес запасов; V — ограничение на емкость склада.

Задача 2. Определить объем запасов V* так, чтобы

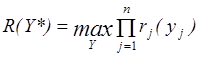(3.26)

или

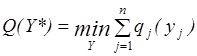, (3.27)

и выполнялись условия

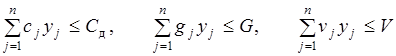(3.28)

гдеС_д— объем средств, выделяемых на создание запасов в каж­дом периоде.

Если ограничение на вес запасов и (или) емкость склада не на­кладывается, то соответствующие неравенства в (3.25) или (3.28) не учитываются.

Рассмотренная математическая модель управления запасами широко используется при определении состава комплектов ЗИПа для технических систем. В этом случае у_j – количество запасных элементов j-го типа, a R(Y) – вероятность достаточности комп­лекта ЗИПа или вероятность нормального функционирования тех­нической системы (без простоев из-за недостачи запасных эле­ментов) .

Рассмотрим пример. Техническая система состоит из n=10 ти­пов элементов, суммарная интенсивность потока отказов элементов каждого типа 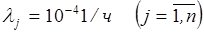, интенсивность потока отказов системы 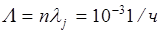. Определить состав комплекта ЗИПа, необходимого для обеспечения нормального функционирования си­стемы в течение времени T=1000 ч с вероятностью R_д ==0,95.

Оптимальный состав комплекта ЗИПа можно определить в ре­зультате решения задачи (3.23) – (3.25), если заданы стоимостные, весовые и габаритные характеристики элементов системы, а также требования к стоимостным (минимум стоимости), весовым G и га­баритным V характеристикам комплекта ЗИПа.

Если указанные характеристики не заданы, то рациональный состав комплекта ЗИПа определяют из условия обеспечения рав­ной вероятности достаточности запасных элементов каждого типа («равнопрочный» ЗИП). Решение задачи производится в следую­щем порядке.

1. Определить требуемые значения вероятности достаточности r_j(y_j) или недостаточности q_j(у_j) из условия

.

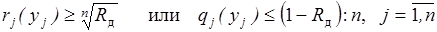Для рассматриваемого примера

.

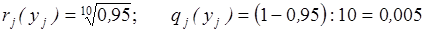2. Вычислить среднее ожидаемое число требований на элемен­ты каждого типа

.

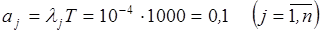3. По формуле (3.18) методом последовательных приближений определить минимальное количество запасных элементов каждого типа, необходимых для обеспечения требуемого значения r_j (у_j).

Так, для рассматриваемого примера 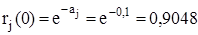; 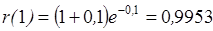, то есть в состав комплекта ЗИПа доста­точно включить по одному элементу каждого типа (всего 10 эле­ментов).

Рассчитаем состав группового комплекта ЗИПа, необходимого для эксплуатации W=5 одинаковых систем для условий рассматриваемого примера. В этом случае 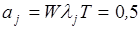. Для обеспечения 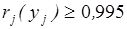в состав комплекта ЗИПа необходимо включить по три запасных элемента каждого типа (всего 30 элементов). Следовательно, создание группового комплекта позволяет уменьшить объем запаса в расчете на одну систему в 10:(30:5)=1,67 раза.

Пусть за счет применения однотипных элементов удалось сократить количество типов элементов до n=5, интенсивность потока отказов системы осталась прежней, то есть .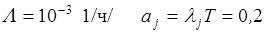

Для обеспечения вероятности 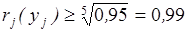в состав индивидуального комплекта необходимо включить по два элемента каждого типа (всего 10 элементов), так как

,

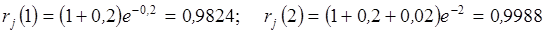а в состав группового комплекта на W=5 систем – по четыре элемента каждого типа (всего 20 комплектов). Групповой комплект эффективнее индивидуального в 10:(20:5)=2,5 раза. Уменьшение числа типов элементов позволило сократить объем запаса в групповом комплекте в 30:20=1,5 раза. Таким образом, при простейшем потоке требований на предметы запаса целесообразно увеличение количества потребителей, обслуживаемых одним складом (создание групповых комплектов ЗИПа), и уменьшение числа используемых номенклатур (числа ЗИПов элементов в технических системах).

При управлении запасами дорогостоящих предметов (стоимость предметов запаса значительно превышает стоимость поставки) целесообразно использовать стратегию двух уровней (T, y) при S= y – y_кр=1. В этом случае заказ подается каждый раз после выдачи потребителю предмета запаса, то есть пополнение является непрерывным.

Рассмотрим случай, когда поток требований на предметы запаса – простейший поток интенсивности λ; время пополнения – случайная величина, распределенная по экспоненциальному со средним значением (μ – интенсивность пополнения), а величина дефицита не может превысить единицу. Этот случай типичен при обеспечении технических систем дорогостоящими запасными элементами (приборами, агрегатами). Если в момент отказа системы в комплекте ЗИПа нет требуемого элемента, то она простаивает и ее элементы не отказывают (дефицит не может превысит единицы). Пополнение комплекта ЗИПа происходит или за счет поставки из органа снабжения или путем ремонта отказавшего прибора.

Для определения вероятности возникновения дефицита постро­им граф состояний СУЗ по одной номенклатуре. При заданном у состояние СУЗ в любой момент времени полностью определяется числом заявок k на предметы запаса, поданных в источник снабжения. Действительно, если СУЗ находится в состоянии S_д (k = 0, 1, . . ., у, у+1), то это означает, что подано k заявок на пред­меты запаса, а на складе имеется у – k предметов запаса (при k = y +1 имеет место дефицит). Переход СУЗ из состояния S_k в состояние S_k+1 (k = 0, 1, . . ., у) происходит под воздействием потока требований интенсивности λ, а переход из S_k в S_k-1 (k=1, 2, . . .,y+1) под воздействием потока поступлений предметов запаса на склад интенсивности k_μ..

Размеченный граф со­стояний изображен на рис. 3.9 и соответствует (y+1)-канальной СМО с отказами. Следовательно, вероятность возникнове­ния дефицита есть вероятность попадания СУЗ в состояние S_у+1а стационарное значение этой вероятности определяется формулами Эрланга (2.36), то есть

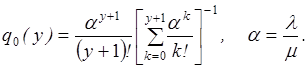(3.29)

Стационарная вероятность достаточности предметов запаса

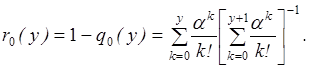(3.30)

Физически q₀(у) – это средняя доля времени, в течение кото­рого на складе имеет место дефицит, а r₀(у) – доля времени, в те­чение которого он отсутствует. Для случая обеспечения техниче­ских систем запасными элементами r₀(у) – составляющая коэффи­циента готовности технической системы, характеризующая своевре­менность обеспечения ее запасными элементами.

Эффективность многономенклатурной СУЗ можно оценить ве­роятностью отсутствия дефицита по всем номенклатурам R₀(Y) или вероятностью возникновения дефицита хотя бы по одной но­менклатуре Q₀(Y) в стационарном режиме функционирования си­стемы

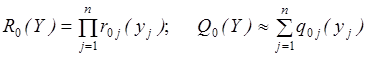. (3.31)

Оптимальные параметры стратегии управления запасами 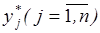можно определить в результате решения задачи (3.23)–(3.25) или (3.26) – (3.28), где вместо R(Y) и Q(Y) исполь­зуют R₀(Y) и Q₀(Y) из формул (3.31). Требуемое значение показа­теля вероятности отсутствия дефицита R_д можно определить ис­ходя из физических особенностей предметов запаса и важности за­дач, решаемых их потребителями. Так, для случая обеспечения тех­нических систем запасными элементами величину R_д можно опре­делить из условия

K_г= R_д K_г0

где К_г – требуемое значение коэффициента готовности; К_г0 – зна­чение коэффициента готовности, вычисленное при условии, что де­фицит на запасные элементы не возникает.