Теоретическая производительность

Центробежного насоса

Впервые основное уравнение центробежных насосов было выведено членом Петербургской академии наук знаменитым математиком и механиком Л. Эйлером.

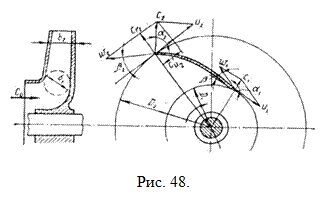
В центробежных насосах жидкость подводится к лопаткам рабочего колеса вдоль оси вала (рис. 48). При входе на лопатки происходит отклонение струй от осевого направления к радиальному. Жидкость на лопатки поступает с абсолютной скоростью , ана внешней окружности рабочего колеса скорость ее достигает величины .

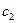Частицы жидкости между лопатками рабочего колеса совершают сложное движение. Во-первых, они участвуют во вращении с окружной переносной скоростью 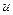и, во-вторых, перемещаются вдоль лопаток с относительной скоростью .

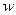Для упрощения принимают, что движение жидкости является струйным, и траектории движения каждой частицы повторяют очертания лопаток. Такое движение возможно было бы при бесконечно большом числе лопаток.

Абсолютная скорость движения жидкости равна геометрической сумме переносной (окружной) и относительной скоростей (параллелограмм скоростей на рис. 48)

. (152)

Следует заметить, что окружная скорость 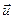направлена по касательной к той окружности, на которой расположена частица, а относительная скорость направлена по касательной к поверхности лопатки в данной точке.

Радиальная составляющая абсолютной скорости на ободе рабочего колеса равна

, (154)

а окружная составляющая

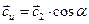, (155)

где 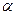– угол между направлением абсолютной скорости и касательной к окружности; 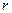– индекс, обозначающий «радиальная»; 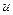– индекс, обозначающий «окружная».

Индексы «1» и «2» приняты для обозначения величин соответственно на входе в рабочее колесо и на выходе из него.

Окружная скорость рабочего колеса на выходе

,

где –диаметр рабочего колеса, м; 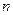–число оборотов в минуту.

Радиальную составляющую абсолютной скорости можно определить исходя из уравнения неразрывности потока

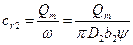, (156)

где 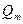–теоретический расход жидкости, проходящий через колесо, м³/сек; 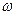– живое сечение на выходе из колеса, м²; –ширина рабочего колеса на выходе, м; 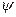– коэффициент стеснения потока лопатками на выходе; его значение для малых насосов принимают равным 0,9 и для больших – 0,95.

Аналогично можно определить величины абсолютной скорости, окружной скорости, угол между направлением относительной скорости и касательной на входе в рабочее колесо. Абсолютная скорость на входе зависит от конструктивных особенностей рабочего колеса; для большинства насосов угол входа при оптимальном режиме назначается равным 90° с таким расчетом, чтобы избежать гидравлического удара; тогда окружная скорость на входе 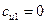(радиальный вход).

Коэффициент стеснения струи на входе по лабораторным исследованиям можно принять для малых насосов равным 0,75, для больших – 0,83.

В целях предотвращения гидравлического удара при поступлении жидкости на рабочее колесо необходимо, чтобы скорость ее не изменялась ни по величине, ни по направлению, т. е. направление относительной скорости при входе должно совпадать с направлением изгиба тела лопатки. Практика и опыт показывают, что при небольшом отклонении угла до 7-8° поток от лопаток не отрывается и поэтому гидравлические потери на удар можно принимать равными нулю. А это позволяет лопатки рабочего колеса у входа выполнять несколько круче, чем из условия безударного входа. Кроме того, входную кромку лопаток округляют.

После рассмотрения предварительных данных можно перейти к выводу основного уравнения центробежного насоса.

Выше было принято, что рабочее колесо имеет бесконечно большое число лопаток, и работа происходит без гидравлических потерь; это позволяет считать, что весь поток в колесе состоит из одинаковых элементарных струек, имеющих форму межлопаточного пространства колеса, и что скорости во всех точках цилиндрической поверхности данного радиуса одинаковы.

Как известно, работа на перемещение жидкости равна

,

где 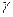– объемный вес жидкости; 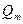–теоретическая производительность; 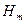– теоретический напор.

Используем уравнение моментов количества движения, которое для установившегося потока можно сформулировать так: изменение момента количества движения массы жидкости, протекающей в единицу времени при переходе от одного сечения к другому, равно моменту внешних сил, приложенных к потоку между этими сечениями. Относя положение к центробежному насосу, можно отметить, что внешние силы прикладываются к потоку под действием лопаток рабочего колеса. За 1 сек через каналы рабочего колеса протекает объем жидкости, численно равный перекачиваемому секундному расходу 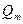;его масса равна

.

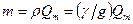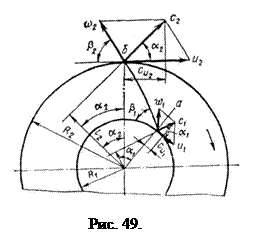
Момент количества движения потока при радиусе у входа в рабочее колесо (рис. 49) равен

. (157)

Здесь – длина перпендикуляра, опущенного из центра колеса на направление скорости .

Соответственно, момент количества движения потока у выхода из колеса при радиусе

. (158)

Таким образом, изменение момента количества движения жидкости, протекающей через колесо за 1 сек, равно

.

Согласно рис. 49

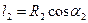и .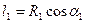

Подставляя эти значения в предыдущее выражение, имеем

.

Умножая обе части уравнения на угловую скорость 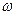, получим

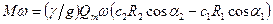, (а)

где –мощность, затраченная на передачу энергии жидкости.

Поток с расходом 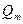переносит в секунду 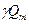жидкости; если при этом жидкость обладает напором 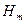, то поток обладает мощностью

. (б)

Следовательно, можно записать

.

Учитывая, что 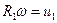и из выражений (а) и (б), получим

.

Поделим обе части уравнения на 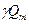и получим основное уравнение теоретического напора

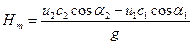. (159)

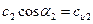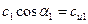Так как и (проекции скоростей), основное уравнение можно написать в следующем виде:

. (160)

Тангенциальная проекция абсолютной скорости 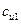представляет собой скорость закручивания потока до поступления его в рабочее колесо. В современных насосах обеспечивается вход на колесо без предварительного закручивания (радиальный вход). Тогда тангенциальная скорость на входе равна нулю и

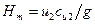. (161)

Уравнение (161) показывает, что напор насоса пропорционален окружной скорости (т. е. числу оборотов и диаметру рабочего колеса) и проекции абсолютной скорости на окружную скорость, т. е. напор тем больше, чем меньше угол 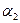и чем больше угол 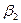(см. рис. 49). Фактически создаваемый насосом напор меньше теоретического, так как часть энергии расходуется на преодоление гидравлических сопротивлений внутри насоса, а также вследствие того, что не все частицы жидкости совершают движение вдоль лопаток, а это вызывает уменьшение абсолютной скорости.

Чтобы учесть конечное число лопаток рабочего колеса и соответственно величину проекции абсолютной скорости на выходе, вводится поправочный коэффициент К. Исходя из изложенного, уравнение для полного напора при конечном числе лопаток можно написать в виде

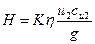, (162)

где К – коэффициент, учитывающий конечное число лопаток; 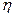– гидравлический к. п. д., зависящий от конструкции насоса и его размеров и принимающий значения 0,8-0,95.

Практически принимают 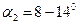и . Принять нельзя, так как тогда радиальная скорость на выходе будет равна нулю, и насос не будет подавать жидкость.

Для определения значения К можно привести одну из формул, полученную академиком Г. Ф. Проскура

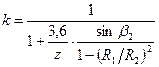, (163)

где 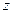– число лопаток.

Обычно 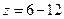, тогда К получается равным 0,75-0,9.

При приближенных расчетах для определения напора в метрах водяного столба (м вод. ст.) можно пользоваться следующим уравнением:

, (164)

где 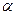–коэффициент напора, принимаемый для насосов турбинного типа, т. е. с направляющим аппаратом, 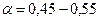, для спиральных насосов 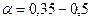; –окружная скорость на внешней окружности рабочего колеса, м/сек. Теоретическую производительность рабочего колеса насоса можно вычислить по формуле

, (165)

где 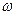– площадь живого сечения потока на выходе из колеса, м²; – средняя радиальная скорость жидкости, м/сек.

Для центробежных насосов площадь живого сечения рабочего колеса (без учета стеснения его лопатками и утечек через неплотности) определяют как боковую поверхность цилиндра с диаметром, равным внешнему диаметру колеса и высотой, равной ширине колеса . Таким образом,

, . (166)

При бесконечно большом числе лопаток радиальная скорость может быть принята одинаковой во всех точках цилиндрической поверхности данного радиуса, а отсюда средняя скорость в уравнении расхода равна радиальной скорости на выходе, т. е. .

Итак, теоретическая производительность равна:

для выходного сечения

, (167)

(без учета стеснения и утечек через неплотности);
для входного сечения

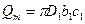; (168)

полезная производительность

, (169)

где 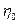– объемный к. п. д. насоса.