Элементарные преобразования строк матрицы

Определение 5.8. Элементарными преобразованиями строк матрицыназывают следующие преобразования:

1) умножение строки матрицы на ненулевое действительное число;

2) прибавление к одной строке матрицы другой её строки, умноженной на произвольное действительное число.

Лемма 5.1.С помощью элементарных преобразований строк матрицы можно поменять местами любые две строки.

Доказательство.

А= .

.

Ступенчатая матрица. Ранг матрицы

Определение 5.9. Ступенчатойбудем называть матрицу, которая обладает следующими свойствами:

1) если i-я строка нулевая, то (i + 1)-я строка также нулевая,

2) если первые ненулевые элементы i-й и (i + 1)-й строк расположены в столбцах с номерами k и R, соответственно, то k < R.

Условие 2) требует обязательного увеличения нулей слева при переходе от i-й строки к (i + 1)-й строке. Например, матрицы

А₁ = , А₂ = , А₃ =

являются ступенчатыми, а матрицы

В₁ = , В₂ = , В₃ =

ступенчатыми не являются.

Теорема 5.1.Любую матрицу можно привести к ступенчатой с помощью элементарных преобразований строк.

Проиллюстрируем эту теорему на примере.

А=

.

Получившаяся матрица – ступенчатая.

Определение 5.10. Рангом матрицыбудем называть число ненулевых строк в ступенчатом виде этой матрицы.

Например, ранг матрицы А в предыдущем примере равен 3.

Вопросы для самоконтроля

1. Что называется матрицей?

2. Как производится сложение и вычитание матриц; умножение матрицы на число?

3. Дайте определение умножению матриц.

4. Какая матрица называется транспонированной?

5. Какие преобразования строк матрицы называются элементарными?

6. Дайте определение ступенчатой матрицы.

7. Что называют рангом матрицы?

Определители

Вычисление определителей

Определители второго порядка

Рассмотрим квадратную матрицу второго порядка

А = .

Определение 6.1. Определителем второго порядка,соответствующим матрице A,называется число, вычисляемое по формуле

│А│= = .

Элементы a_ij называются элементами определителя│A│, элементы а₁₁, а₂₂ образуют главную диагональ, а элементы а₁₂, а₂₁ – побочную.

Пример. = –28 + 6 = –22.

Определители третьего порядка

Рассмотрим квадратную матрицу третьего порядка

А = .

Определение 6.2. Определителем третьего порядка,соответствующим матрице А, называется число, вычисляемое по формуле

│А│= = .

Чтобы запомнить, какие произведения в правой части равенства следует брать со знаком «плюс», а какие ─ со знаком «минус», полезно запомнить правило, называемое правилом треугольника:

=─

Пример.

1) = –4 + 0 + 4 – 0 + 2 + 6 = 8.

2) = 1, т. е. │Е₃│= 1.

Рассмотрим ещё один способ вычисления определителя третьего порядка.

Определение 6.3. Минором M_ijэлементаa_ij определителя называется определитель, полученный из данного вычёркиванием i-й строки и j-го столбца. Алгебраическим дополнениемA_ij элемента a_ij определителя называется его минор M_ij, взятый со знаком (–1)^i+j.

Пример.Вычислим минор М₂₃ и алгебраическое дополнение А₂₃ элемента а₂₃ в матрице

А = .

Вычислим минор М₂₃:

М₂₃ = = = –6 + 4 = –2.

Тогда А₂₃ = (–1)²⁺³М₂₃ = 2.

Теорема 6.1. Определитель третьего порядка равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения.

Доказательство. По определению

= . (6.1)

Выберем, например, вторую строку и найдём алгебраически дополнения А₂₁, А₂₂, А₂₃:

А₂₁ = (–1)²⁺¹ = –( ) = ,

А₂₂ = (–1)²⁺² = ,

А₂₃ = (–1)²⁺³ = –( ) = .

Преобразуем теперь формулу (6.1)

│А│= ( ) + ( ) + ( ) =

= А₂₁ + А₂₂ + А_23.

Формула А│= А₂₁ + А₂₂ + А_23. называется разложением определителя│А│ по элементам второй строки. Аналогично разложение можно получить по элементам других строк и любого столбца

Пример.

= (по элементам второго столбца) = 1× (–1)¹⁺² + 2 × (–1)²⁺² +

+ (–1)(–1)³⁺² = –(0 + 15) + 2(–2 +20) + (–6 +0) = –15 +36 – 6 = 15.

6.1.3 Определители n-го порядка 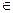(n N)

Определение 6.4. Определителем n-го порядка,соответствующим матрице n-го порядка

А =

называется число, равное сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения, т. е.

│A│= А_i1 + A_i2 + … + A_in = А_1j + A_2j + … + A_nj .

Нетрудно заметить, что при n = 2 получается формула для вычисления определителя второго порядка. Если n = 1, то по определению будем считать |A| = |a | = a .

Пример. = (по элементам 4-й строки) = 3×(–1)⁴⁺² +

+ 2×(–1)⁴⁺⁴ = 3(–6 + 20 –2 –32) +2(– 6 +16 +60 +2) = 3(–20) +2×72 = –60 +144 = 84.

Заметим, что если в определителе все элементы какой-либо строки (столбца), кроме одного, равны нулю, то при вычислении определителя его удобно разложить по элементам этой строки (столбца).

Пример.

│Е_n│= = 1 × │E_n-1│ = … = │E₃│= 1.

Свойство определителей

Определение 6.5. Матрицу вида

или

будем называть треугольной матрицей.

Свойство 6.1. Определитель треугольной матрицы равен произведению элементов главной диагонали, т. е.

= = .

Свойство 6.2. Определитель матрицы с нулевой строкой или нулевым столбцом равен нулю.

Свойство 6.3.При транспонировании матрицы определитель не изменяется, т. е.

│А│= │А^t│.

Свойство 6.4.Если матрица В получается из матрицы А умножением каждого элемента некоторой строки на число k, то

│В│= k│А│.

Свойство 6.5.

= + .

Свойство 6.6.Если матрица В получается из матрицы А перестановкой двух строк, то│В│= −│А│.

Свойство 6.7.Определитель матрицы с пропорциональными строками равен нулю, в частности, нулю равен определитель матрицы с двумя одинаковыми строками.

Свойство 6.8.Определитель матрицы не изменяется, если к элементам одной строки прибавить элементы другой строки матрицы, умноженные на некоторое число.

Замечание. 6.1. Так, как по свойству 6.3 определитель матрицы не меняется при транспонировании, то все свойства о строках матрицы верны и для столбцов.

Свойство 6.9.Если А и В – квадратные матрицы порядка n, то │АВ│=│А││В│.

Обратная матрица

Определение 6.6.Квадратная матрица А порядка n называется обратимой,если существует матрица В такая, что АВ = ВА = Е_n. В этом случае матрица В называется обратной к матрицеА и обозначается А^–1.

Теорема 6.2.Справедливы следующие утверждения:

1) если матрица А обратима, то существует точно одна ей обратная матрица;

2) обратимая матрица имеет определитель, отличный от нуля;

3) если А и В – обратимые матрицы порядка n, то матрица АВ обратима, причём (АВ)^–1 = В^–1 ×А^–1.

Доказательство.

1. Пусть В и С – матрицы, обратные к матрице А, т. е. АВ = ВА = Е_n и АС = СА = Е_n. Тогда В = ВЕ_n = В(АС) = (ВА)С = Е_nС = С.

2. Пусть матрица А обратима. Тогда существует матрица А^–1, ей обратная, причём

АА^–1 = Е_n.

По свойству 6.9 определителя │АА^–1│=│А││А^–1│. Тогда │А││А^–1│=│Е_n│, откуда │А││А^–1│= 1. Следовательно, │А│¹ 0.

3. Действительно,

(АВ)(В^–1А^–1) = (А(ВВ^–1))А^–1 = (АЕ_n)А^–1 = АА^–1 = Е_n.

(В^–1А^–1)(АВ) = (В^–1(А^–1А))В = (В^–1Е_n)В = В^–1В = Е_n.

Следовательно, АВ – обратимая матрица, причём (АВ)^–1 = В^–1А^–1.

Следующая теорема даёт критерий существования обратной матрицы и способ её вычисления.

Теорема 6.3. Квадратная матрица А обратима тогда и только тогда, когда её определитель отличен от нуля. Если │А│¹ 0, то

А^–1 = .

Пример. Найти матрицу, обратную для матрицы А = .

Решение.│А│= = 6 + 1 = 7.

Так как │А│¹ 0, то существует обратная матрица

А^–1 = = .

Вычисляем А₁₁ = 3, А₁₂ = 1, А₂₁ = –1, А₂₂ = 2. Тогда А^–1 = .

Вопросы для самоконтроля

1. Что называется определителем?

2. Каковы его основные свойства?

3. Что называется минором и алгебраическим дополнением?

4. Каковы способы вычисления определителей (второго, третьего и n-го порядков)?

5. Какая матрица называется квадратной?