Уравнения динамики материальной точки

Под материальной точкой будем понимать тело, размерами которого можно пренебречь.

Если в некоторой ИСО ускорение материальной точки равно нулю, то оно равно нулю и в любой другой ИСО. Это значит, что закон инерции Ньютона инвариантен относительно преобразований Лоренца. С другой стороны, уравнения динамики не инвариантны относительно этих преобразований и требуют обобщения.

Инерционные свойства тела или частицы можно охарактеризовать некоторым скаляром - инвариантной массой или массой покоя m. Масса покоя является константой, характерной для каждого вида элементарных частиц.

Определим 4-импульс частицы 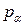соотношением

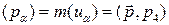, (1)

или, в компонентах,

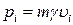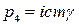; , (2)

где, напомним, 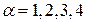, 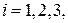а

.

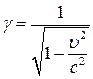Очевидно, уравнения (2) для пространственных компонент можно объединить в одно векторное равенство

,

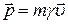которое в предельном случае 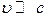переходит в обычную формулу классической механики для вектора импульса

.

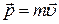Естественным релятивистским обобщением уравнений динамики Ньютона являются уравнения

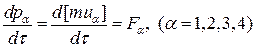(3)

где 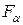– некоторый 4-х мерный вектор, называемый 4-х мерной силой или силой Минковского.

Очевидно, эти уравнения релятивистски инвариантны. Их называют уравнениями релятивистской динамики. Запишем их отдельно для пространственных и временной компонент:

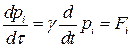, (i=1,2,3),

или

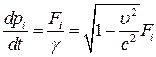, (4)

При 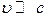эти уравнения должны превращаться в обычные уравнения Ньютона.

В левой части (4) стоит производная от импульса по обычному времени. Потребуем, чтобы справа стояли компоненты 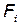обычной силы 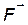. Тогда формулу (4) можно переписать в виде

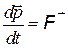, (5)

причем

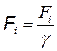, i=1,2,3. (6)

Как и требуется, при 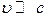(5) переходит в обычное уравнение Ньютона. Для временной компоненты получим

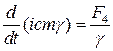. (7)

Чтобы выяснить физический смысл 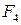, найдем

.

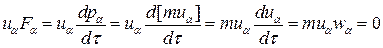Следовательно, 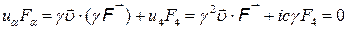, и

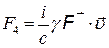. (8)

Подставляя (8) в (7), получим

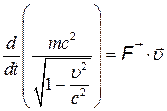, (6)

В правой части 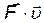дает работу силы над частицей, производенную в единицу времени, поэтому в левой части стоит изменение энергии в единицу времени. Естественно определить энергию частицы соотношением

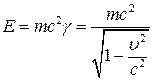, (7)

Ее обычно называют полной энергией, хотя она не включает потенциальную энергию частицы во внешнем поле.

Найдем выражение для трехмерного ускорения 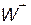частицы. Имеем

,

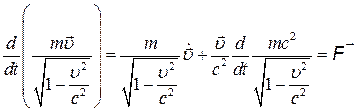откуда

.
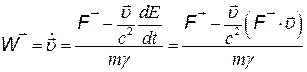