Локальная геометрическая теория динамики
Идеи современной нелинейной динамики часто представляют в геометрической форме или в виде рисунков. Например, движение осциллятора без затухания 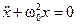 , можно представить на фазовой плоскости
, можно представить на фазовой плоскости 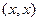 в виде эллипса. На таком рисунке время представлено неявно, и временная эволюция описывается движением вдоль эллипса по часовой стрелке. Размер эллипса зависит от задания начальных условий для
в виде эллипса. На таком рисунке время представлено неявно, и временная эволюция описывается движением вдоль эллипса по часовой стрелке. Размер эллипса зависит от задания начальных условий для 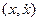 .
.
При исследовании нелинейных задач сначала следует найти точки равновесия системы, а затем рассмотреть движение вокруг каждого положения равновесия. Локальное движение характеризуется свойствами собственных значений линеаризованной системы.
Если динамическую модель можно представить в виде системы дифференциальных уравнений первого порядка 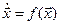 ,где
,где 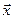 – вектор, компоненты которого – параметры состояния, то точки равновесия определяются равенством
– вектор, компоненты которого – параметры состояния, то точки равновесия определяются равенством 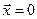 , или
, или 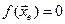 .
.
Например, в случае гармонического осциллятора имеется только одна точка равновесия, расположенная в начале координат: 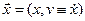 ,
, 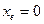 ,
, 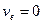 . Для выяснения характера поведения вблизи
. Для выяснения характера поведения вблизи 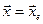 следует разложить функцию
следует разложить функцию 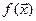 в ряды Тейлора вблизи каждой точки равновесия
в ряды Тейлора вблизи каждой точки равновесия 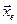 и рассмотреть линеаризованные задачи.
и рассмотреть линеаризованные задачи.
В качестве примера рассмотрим систему двух уравнений первого порядка 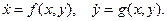
Если время не входит явно в функции 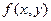 и
и 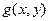 , то задача называется автономной. Координаты точек равновесия должны удовлетворять двум уравнениям:
, то задача называется автономной. Координаты точек равновесия должны удовлетворять двум уравнениям: 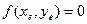 и
и 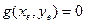 . Вводя малые отклонения от каждого из положений равновесия, т. е.
. Вводя малые отклонения от каждого из положений равновесия, т. е. 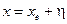 и
и 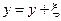 , перепишем систему в виде
, перепишем систему в виде
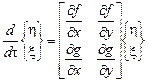 ,
,
где производные вычисляются в точке 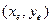 .
.
Характер движения вблизи каждой из точек равновесия выясняется с помощью собственных решений
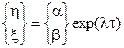 ,
,
где 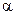 и
и 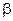 – постоянные.
– постоянные.
Движения классифицируются на основе того, действительно или комплексно 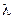 , и в зависимости от знака действительной части
, и в зависимости от знака действительной части 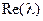 .
.
Траектории на фазовой плоскости при разных собственных значениях показаны на рисунке. К примеру, седловая точка возникает, когда оба собственных значения 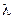 действительны, но
действительны, но 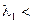 0, а
0, а 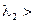 0. Спираль соответствует случаю, когда
0. Спираль соответствует случаю, когда 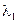 и
и 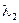 комплексно-сопряженные.
комплексно-сопряженные.
Устойчивость решения линеаризованной системы определяется знаком 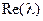 . Когда действительная часть одного из чисел
. Когда действительная часть одного из чисел 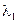 или
или 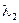 положительна, движение вблизи этой точки равновесия неустойчиво.
положительна, движение вблизи этой точки равновесия неустойчиво.
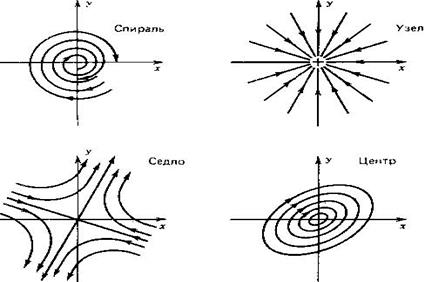
Рисунок 1.60 - Классические фазовые портреты окрестностей четырех различных типов точек равновесия системы двух дифференциальных уравнений, не содержащих явной зависимости от времени
Если корни не являются чисто мнимыми, то локальное движение, описываемое линеаризованной системой, подобно движению исходной нелинейной системы.
Чисто колебательное движение линеаризованной системы 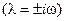 делает необходимым дальнейший анализ для выяснения вопроса об устойчивости нелинейной системы. Эти идеи, изложенные для системы второго порядка, можно обобщить на случай фазового пространства большей размерности.
делает необходимым дальнейший анализ для выяснения вопроса об устойчивости нелинейной системы. Эти идеи, изложенные для системы второго порядка, можно обобщить на случай фазового пространства большей размерности.
