А. Работа, энергия. Законы сохранения

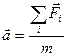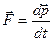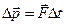; ( ) – второй закон Ньютона;

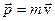– импульс тела;

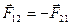– третий закон Ньютона;

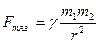– закон всемирного тяготения;

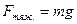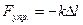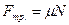; ; – силы тяжести, упругости и трения;

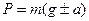– вес тела;

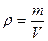– плотность тела;

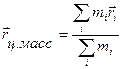– радиус-вектор центра масс.

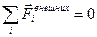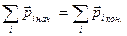Если , то – закон сохранения импульса;

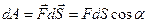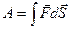; – работа силы;

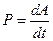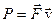; мощность;

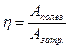– коэффициент полезного действия;

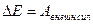; Е_полн.1=Е_полн.2+А_{системы против внешних сил} – закон изменения полной энергии системы;

Е_мех.1=Е_мех.2+А_{системы против внешних сил}+А_{системы против диссипативных сил} – закон изменения механической энергии;

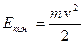– кинетическая энергия поступательного движения;

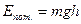– потенциальная энергия тела, поднятого над Землей на небольшую высоту (h<<R_Земли);

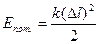– потенциальная энергия упруго деформированного тела; 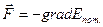( 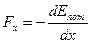) – связь потенциальной энергии и консервативной силы.

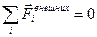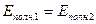Если , то – закон сохранения полной энергии.

Если 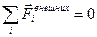и отсутствуют диссипативные силы, то 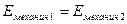– закон сохранения механической энергии.

Б. Упругие свойства твердых тел

ε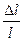_׀׀= – относительное удлинение;

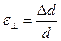– относительное поперечное сжатие;

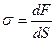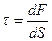( ) – нормальное (тангенциальное) механическое напряжение;

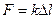; ε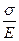_׀׀= – закон Гука;

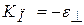/ ε_׀׀ – коэффициент Пуассона;

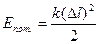– потенциальная энергия упруго деформированного тела;

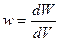– объёмная плотность энергии;

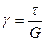– закон Гука для деформации сдвига; где γ – деформация сдвига (угол сдвига);

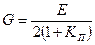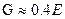; – связь между модулем Юнга и модулем сдвига.

Таблица 1. Механические свойства твёрдых тел

Вещество	Плотность ρ, кг/м3	Модуль Юнга, Е.10-10 Па	Предел прочности, σпр.10-8 Па
Алюминий		6.9	1.1
Железо		19.6
Латунь		-	-
Медь		11.8	2.4
Платина		-	-
Сталь		21.6	7.85
Цинк		-	-

Примеры решения задач

Задача 4.

С поверхности Земли вертикально вверх пущена ракета со скоростью 5 км/с. На какую высоту она поднимется?

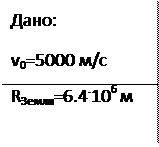Решение

На ракету действует сила притяжения Земли, которая по закону всемирного тяготения равна:

,

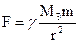где m – масса ракеты, М_З – масса Земли, r=R_Земли+h – расстояние до центра Земли. Элементарная работа против силы тяжести при перемещении ракеты вверх на dr равна: dA=Fdr; полная работа при перемещении ракеты от поверхности Земли до высоты h рассчитывается интегрированием:

.

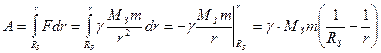По закону сохранения энергии кинетическая энергия, которой обладала ракета на Земле, будет израсходована на работу против силы притяжения: 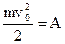. Тогда получим уравнение:

.

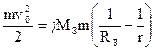После сокращения на m и подстановки r=R_Земли+h получим выражение для высоты:

.

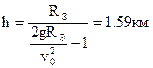Здесь учтено, что 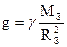- ускорение свободного падения на поверхности Земли.

Ответ: h=1.59 км.

Задача 5.

Однородный медный стержень длиной 1 м равномерно вращается вокруг горизонтальной оси, проходящей через один из его концов. При какой частоте вращения стержень разорвется?

Решение

Найдем зависимость силы натяжения F стержня от координаты x. На расстоянии x от оси вращения выделим фрагмент стержня бесконечно малой длины dx и массой

dm=ρSdx.

На него действуют силы: сила натяжения стержня F – вверх, сила натяжения стержня F+dF (со стороны нижней части стержня) – вниз и сила тяжести gdm – тоже вниз (рис.2). Запишем второй закон Ньютона для массы dm:

adm= F–(F+dF)– gdm,

где а=ω²x – центростремительное ускорение. Отсюда

dF=–dm(g+ ω²x)= –ρSdx(g+ ω²x),

или:

.

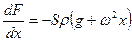Зависимость F(x) теперь можно найти, интегрируя предыдущее выражение или найдя первообразную от выражения ( 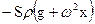) и учтя очевидное граничное условие: F(l)=0:

.

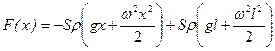Максимальное натяжение будет при x=0:

,

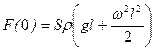а соответствующее механическое напряжение приравняем к пределу прочности:

.

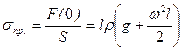Решаем полученное уравнение относительно угловой скорости и затем находим частоту:

.

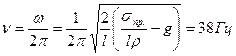Ответ: ν=38 Гц.

61. Камень, пущенный по поверхности льда со скоростью 2 м/с, прошел до полной остановки расстояние 20.4 м. Найти коэффициент трения камня по льду.

62. Граната, летящая со скоростью 10 м/с, разорвалась на два осколка. Больший осколок, масса которого составляла 60% массы всей гранаты, продолжал двигаться в прежнем направлении, но с увеличенной скоростью, равной 25 м/с. Найти скорость меньшего осколка.

63. На железнодорожной платформе установлено орудие. Масса платформы с орудием 15 тонн. Орудие стреляет под углом 60⁰ к горизонту в направлении движения. Какую скорость приобретет платформа вследствие отдачи, если масса снаряда 20 кг, а его скорость 600 м/с?

64. Камень шлифовального станка имеет на рабочей поверхности скорость 30 м/с. Обрабатываемая деталь прижимается к камню с силой 100 Н, коэффициент трения 0.2. Какая мощность затрачивается на шлифовку?

65. Пуля массой 10 г, летящая с горизонтальной скоростью 400 м/с, попадает в мешок с ватой массой 4 кг, висящий на длинной нити. Определить, на какую высоту поднимется мешок, если пуля застрянет в нем, и долю кинетической энергии, которая будет израсходована на пробивание ваты.

66. Шар массой 10 кг сталкивается с шаром массой 4 кг. Скорость первого шара 4 м/с, второго – 12 м/с. Найти общую скорость шаров после удара в двух случаях: 1) когда малый шар догоняет большой шар, движущийся в том же направлении; 2) когда шары движутся навстречу друг другу. Удар прямой, центральный, абсолютно неупругий.

67. Если на верхний конец вертикально расположенной пружины положить груз, то она сожмется на 3 мм. На сколько сожмет пружину тот же груз, упавший на верхний конец пружины с высоты 8 см?

68. Молот массой 5 кг ударяет по небольшому куску железа, лежащему на наковальне. Масса наковальни 100 кг. Удар абсолютно неупругий. Определить КПД удара молота при данных условиях. Массой куска железа пренебречь.

69. Тело массой 0.5 кг движется прямолинейно, причем координата изменяется по закону x=A–Bt+5t²–t³ (время – в секундах, координата – в метрах). Найти силу, действующую на тело в конце первой секунды движения.

70. Стальной шарик массой 20 г, падая с высоты 1 м на стальную плиту, отскакивает от нее на высоту 81 см. Найти импульс силы, полученный плитой за время удара, и количество теплоты, выделившейся при ударе.

71. Какую работу нужно выполнить для того, чтобы равномерно передвинуть по полу ящик массой 50 кг на 4.5 м, нажимая на него руками под углом 30 градусов к горизонту? Коэффициент трения 0.2.

72. Пуля массой 9 г, летящая со скоростью 500 м/с, попадает в доску, установленную перпендикулярно направлению полета пули, и углубляется в нее на 6 см. Определить среднюю силу сопротивления доски движению пули.

73. Две пружины жесткостью 0.5 кН/м и 1 кН/м скреплены параллельно. Определить потенциальную энергию данной системы при абсолютной деформации 4 см. Решить ту же задачу для последовательно соединенных пружин.

74. Самолет массой 2 тонны летит на высоте 500 м со скоростью 80 м/с. Летчик выключает двигатель, и самолет в планирующем полете достигает поверхности земли, касаясь ее со скоростью 40 м/с. Определить работу сил сопротивления во время спуска самолета.

75. При растяжении медной проволоки, поперечное сечение которой равно 1.5 мм², начало остаточной деформации наблюдалось при нагрузке 4.5 кг. Каков предел упругости материала проволоки?

76. Каким должен быть предельный диаметр стального троса, чтобы он выдержал нагрузку 1 т?

77. Найти относительное изменение плотности цилиндрического медного стержня при сжатии его давлением 10⁸ Па. Коэффициент Пуассона для меди принять равным 0.34.

78. К стальной проволоке радиусом 1 мм подвешен груз 100 кг. На какой наибольший угол можно отклонить проволоку с грузом, чтобы она не разорвалась при прохождении этим грузом положения равновесия?

79. Какой наибольший груз может выдержать стальная проволока диаметром 1мм, не выходя за предел упругости 294 МПа? Какую долю первоначальной длины составляет удлинение проволоки при этом грузе?

80. К вертикальной проволоке длиной 5м и площадью поперечного сечения 2 мм² подвешен груз массой 5.1кг. В результате проволока удлинилась на 0.6 мм. Найти модуль Юнга материала проволоки.

81. К стальному стержню длиной 3 м и диаметром 2 см подвешен груз массой 25 тонн. Определить напряжение в стержне, относительное и абсолютное удлинения стержня.

82. Какую работунужно совершить, чтобы растянуть на 1 мм стальной стержень длиной 1 м и площадью поперечного сечения, равной 1 см²?

83. Стержень из стали длиной 2 м и площадью поперечного сечения 2 см² растягивается некоторой силой, причем удлинение равно 0.4 см. Вычислить потенциальную энергию растянутого стержня и объемную плотность энергии.

84. На какую высоту поднимается камень массой 30г, выпущенный вертикально вверх из рогатки, резиновый жгут которой сечением 0.2 см² и длиной 30 см был растянут на 20 см? Сопротивление воздуха не учитывать. Модуль Юнга для резины 7.8 МПа.

85. Определить относительное удлинение алюминиевого стержня, если при его растяжении затрачена работа6.9 Дж. Длина стержня 1 м, площадь поперечного сечения 1 мм² модуль Юнга для алюминия 69 ГПа.

86. Горизонтальный железный стержень длиной 150 см вращается около вертикальной оси, проходящей через его середину. При какой частоте оборотов он может разорваться?

87. Гирька весом 4.9 Н, привязанная к резиновому шнуру, описывает в горизонтальной плоскости окружность. Частота вращения гирьки 2 Гц. Угол отклонения резинового шнура от вертикали равен 30°. Найти длину нерастянутого резинового шнура. Для растяжения шнура на 1 см требуется сила 6.0 Н.

88. Найти энергию упругой деформации стального стержня массой 3.1 кг, который растянут так, что его относительное удлинение равно 1.0×10^-3.

89. Железная проволока длиной 5 м висит вертикально. На сколько изменится объем проволоки, если к ней привязать гирю массой 10 кг? Коэффициент Пуассона для железа принять равным 0.3.

90. Определить работу растяжения стальной проволоки длиной 2 м и радиусом 3 мм под действием груза 200 кг.