Программируем функцию для вычисления факториала

Постановка задачи

Проверим численным методом «справедливость» формулы бинома Ньютона. Эта формула была известна ещё индийским и исламским математикам.

Определения:

1. Факториалчисла n (лат. factorialis — действующий, производящий умножающий; обозначается n!, произносится эн факториа́л) — произведение всех натуральных чисел от 1 до n включительно:

Например:

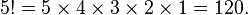
По определению полагают 0! = 1. Факториал определён только для целых неотрицательных чисел.

2. Бином Ньютона - формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных

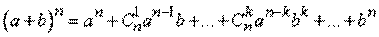
где

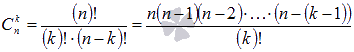
–биномиальные коэффициенты (число всех возможных сочетаний, которые можно образовать из n элементов по k), 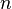— неотрицательное целое число, а и b — какие угодно числа.

Выражение, которое находится в правой части формулы бинома Ньютона, называют разложением выражения (a+b)ⁿ, а выражение 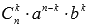называют (k+1)-ым членом разложения, k=0,1,2,…,n.

Ньютон вывел формулу бинома для более общего случая, когда показатель степени – произвольное рациональное число (возможно, отрицательное). В этом случае бином представляет собой бесконечный ряд.

Частными случаями бинома Ньютона при n = 2 и n = 3 являются известные формулы для квадрата и куба суммы а и b:

(а + b)² = а² + 2ab + b² ;

(а + b)³ = а³ + 3a²b + 3ab² + b³;

Пример:
(a + b)⁵ = a⁵ + C¹₅ a⁴b + C²₅ a³b² + C³₅ a²b³ + C⁴₅ ab⁴ + C⁵₅ b⁵ = a⁵ + 5a⁴b + 10a³b² + 10a²b³ + 5ab⁴ + b⁵

Треугольник Паскаля.

Биномиальные коэффициенты для различных n удобно представлять в виде таблицы, которая называется арифметический треугольник Паскаля. В общем виде треугольник Паскаля имеет следующий вид:

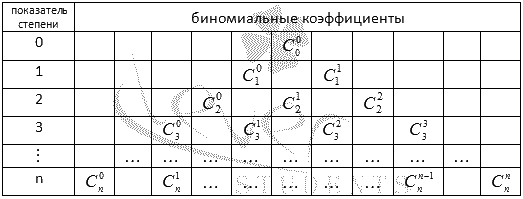
Треугольник Паскаля чаще встречается в виде значений коэффициентов бинома Ньютона для натуральных n:

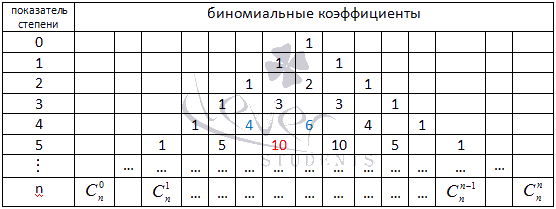
Боковые стороны треугольника Паскаля состоят из единиц. Внутри треугольника Паскаля стоят числа, получающиеся сложением двух соответствующих чисел над ним. Например, значение десять (выделено красным) получено как сумма четверки и шестерки (выделены голубым). Это правило справедливо для всех внутренних чисел, составляющих треугольник Паскаля, и объясняется свойствами коэффициентов бинома Ньютона.

Разрабатываем программу

1. Создаем проект и сохраняем его (Save Project As…)

ФайлUnit 1.cpp – сохраняем с именем Main

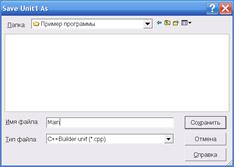
Файл Project1сохраняем под именем, как хотим называть файл – exe (Binom).

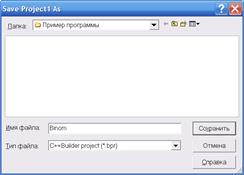
Компилируем программу и убеждаемся, что проект создан правильно

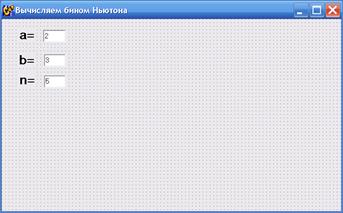
3. Помещаем на форму три компонента Edit из закладки «Standart» и в свойстве «Text» компонентов записываем нужные нам числа

Создаем новый модуль Unit

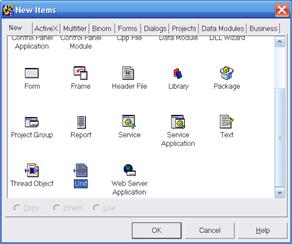
и сохраняем его под именем «Function» ( в меню пункт «Save»)

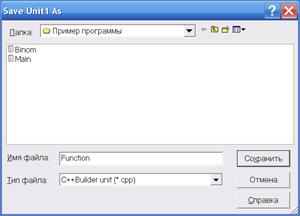
Имеем такой модуль

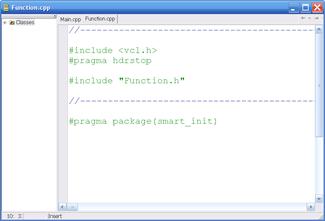
Программируем функцию для вычисления факториала

int Factorial ( int n )

{

int F =1;

for ( int i =2; i < n+1; i ++)

F = F*i;

return F;

}