Метод динамического программирования

Согласно результатам теоремы 1, пользуясь условиями (9.2.5), (9.2.6), мы можем последовательно определить функции 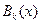и их области определения .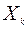

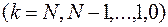Действительно, 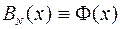, 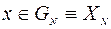– известны.

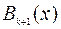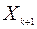
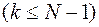Пусть известны и . Для определения нужно решить задачу минимизации функции

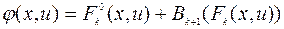
по переменным 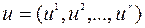на известном множестве

.

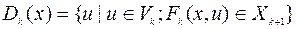Для решения этой задачи могут быть использованы методы НЛП. Функция определена в точке 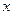тогда и только тогда, когда 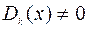. Следовательно, при определении значения функции одновременно находится и область ее определения

.

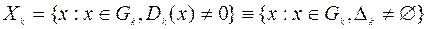Так как 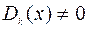хотя бы при одном , то .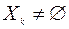

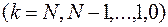Предположим, что из условий (9.2.5), (9.2.6) найдены функции и пусть также известны функции 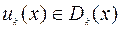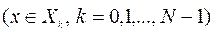на которых достигается нижняя грань в правой части (9.2.5). Тогда несложно выписать решение задач (9.1.5)-(9.1.8) и (9.2.1)-(9.2.4).

Оптимальное управление – 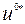, оптимальная траектория – 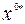задачи (9.1.5)–(9.1.8) определяются следующим образом: сначала из условия

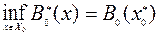(9.3.1)

находим 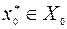. Затем, используя зависимости 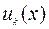и (9.1.6) последовательно определяем оптимальное управление и оптимальную траекторию

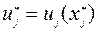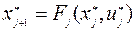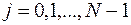, , . (9.3.2)

Оптимальное управление – 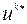, оптимальная траектория – 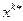задачи (9.2.1)–(9.2.4) определяются по формулам, аналогичным (9.3.2), при этом фиксируется начальное состояние:

1) 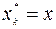; 2) 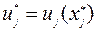, , 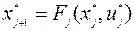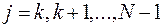. (9.3.3)

Сформулируем отмеченные результаты в виде соответствующих теорем. Первая из теорем устанавливает взаимосвязь оптимального решения и рекуррентных соотношений Беллмана.

Теорема 2. Пусть из соотношений (9.2.6), (9.2.5) последовательно определены функции и их области определения 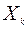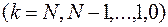, а также функции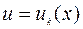 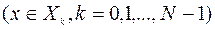, на которых достигается нижняя грань в уравнении (9.2.5), и пусть 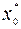определено условием (9.3.1). Тогда оптимальное управление 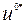и оптимальная траектория 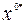задачи (9.1.5)–(9.1.8) определяются соотношениями (9.3.1)–(9.3.2).

В теории оптимального управления и ее приложениях важное место занимает так называемая проблема синтеза, заключающаяся в построении функции 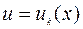, выражающей собой оптимальное управление при условии, что в момент 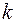объект находится в точке 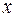фазового пространства. Следующая теорема показывает, что решение уравнения Беллмана (9.2.5) равносильно решению проблемы синтеза для задачи (9.2.5)-(9.2.8). А именно, функция 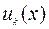, на которой достигается нижняя грань в (9.2.5), является синтезирующей: если в момент 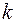объект находится в точке 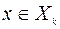, то дальнейшее оптимальное движение объекта определяется условиями:

, .

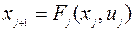
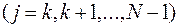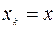Теорема 3. Пусть из соотношений (9.2.6), (9.2.5) последовательно определены функции и их области определения 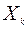, а также функции 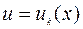, на которых достигается нижняя грань в уравнении (9.2.5). Тогда оптимальное управление 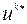и оптимальная траектория 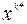задачи (9.2.1)–(9.2.4) определяются формулами (9.3.3).

Согласно результатам теоремы 3 оптимальное управление 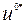задачи (9.1.5)–(9.1.8) обладает тем свойством, что для произвольного 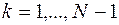оптимальное управление 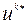и оптимальная траектория 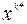* задачи (9.2.1)–(9.2.4)при заданном начальном состоянии 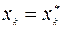совпадают с отрезками оптимального управления 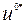и оптимальной траекторией 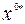задачи (9.1.5)–(9.1.8). Последнее утверждение является одной из формулировок принципа оптимальности.

Существуют задачи типа (9.1.5)-( 9.1.8), когда нижняя грань в (9.2.5) или (9.3.1) не достигается. В таких задачах приходится пользоваться величинами, лишь приближенно реализующими нижнюю грань.