Скалярное произведение векторов
10.1. Найти скалярное произведение векторов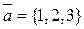 
и 
.
10.2. Даны точки 
. Найти косинус угла между векторами 
и 
.
10.3. Найти косинус угла между векторам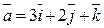и 
и 
.
10.4. Даны векторы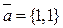 
, 
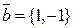и их представление через векторы 
и 
: 
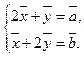. Найти косинус угла между векторами и .
10.5. Найти проекцию вектора 
на направление вектора 
.
10.6. Даны векторы 
, 
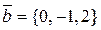. При каком 
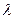векторы 
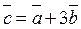и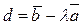 
ортогональны?
10.7. Даны вершины треугольника A(-3.-2,0), B(0,-2,4) и C(4,-2,1). Найти угол 
.
10.8. Найти вектор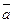 
, коллинеарный вектору 
и удовлетворяющий условию 
.
10.9. Доказать, что если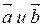 
- единичные векторы, то их линейные комбинации
и 
, где 
, перпендикулярны между собой тогда и только тогда, когда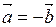 
.
10.10. Используя скалярное произведение векторов, доказать теорему косинусов.
10.11. Выразить длины медиан треугольника через длины его сторон.
10.12. Доказать, что сумма квадратов диагоналей параллелограмма равна сумме квадратов длин его сторон.
10.13. Боковые стороны трапеции перпендикулярны между собой. Доказать, что сумма квадратов длин ее диагоналей равна сумме квадратов длин оснований.
10.14. Доказать, что сумма квадратов длин диагоналей любого четырехугольника равна сумме квадратов длин его сторон без учетверенного квадрата длины отрезка, соединяющего середины диагоналей.
10.15. Суммы квадратов длин противоположных ребер тетраэдра равны между собой. Доказать, что противоположные ребра перпендикулярны друг другу.
Занятие № 11.
Векторное и смешанное произведение векторов.
11.1. Вычислить площадь треугольника с вершинами A(4,6,-2), B(7,4,4), C(1,1,6).
11.2. Найти высоту и площадь параллелограмма, построенного на векторах 
и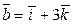 
.
11.3. Даны точки A(2,-1,3), B(1,2,0) и C(3,2,2). Найти координаты векторных произведений: а)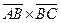 
; б) 
.
11.4. Вычислить площадь параллелограмма, построенного на векторах 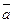и 
:
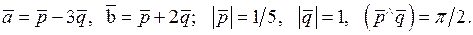
11.5. Вычислить площадь параллелограмма, построенного на векторах 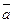и :
11.6. Найти координаты вектора , если известно, что он перпендикулярен векторам 
и 
, образует с ортом 
тупой угол и 
.
11.7. Определить являются ли векторы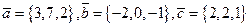 
компланарными.
11.8. Показать, что векторы 
, 
, 
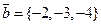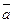компланарны и разложить вектор по векторам и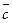 
.
11.9. Определить, лежат ли точки А(1,0,1), В(4,4,6), С(2,2,3), D(10,14,17) в одной плоскости?
11.10. При каком 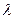векторы 
, 
, 
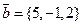компланарны?
11.11. Найти объем параллелепипеда, построенного на векторах 
, 
, 
.
11.12. Даны вершины тетраэдра A(5,2,1), B(2,5,1), С(1,2,5) и D(0,0,1). Вычислить объем тетраэдра, площадь грани ABC и высоту, опущенную на эту грань.
11.13. Даны три вершины тетраэдра A(3,0,1), B(2,1,3), С(2,-1,-1). Найти координаты четвертой вершины D, если известно, что она лежит на оси ординат, а объем тетраэдра равен 5.
11.14. Найти смешанное произведение векторов:
а) 
;
б) 
;
в) 
.
11.15. Дана треугольная призма 
. Найти ее объем, если:
а) 
;
б) 
.
Занятие № 12.
Прямая на плоскости.
12.1. Вычислить угловой коэффициент k прямой, проходящей через две точки А(5, -3) и В(-1, 6).
12.2. Составить уравнение прямой, параллельной двум прямым 
, 
и проходящей посередине между ними.
12.3. Дана прямая 
. Составить уравнение прямой, проходящей через точку А(2, 1) параллельно данной прямой.
12.4. Дана прямая 
. Составить уравнение прямой, перпендикулярной к данной прямой и проходящей через точку А(2, 3).
12.5. Даны уравнения двух сторон прямоугольника 
, 
и уравнение одной из его диагоналей 
. Найти вершины прямоугольника.
12.6. Вычислить величину отклонения d и расстояние d точки А(-2, 3) от прямой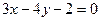 
.
12.7. Привести общее уравнение прямой 
к нормальному виду.
12.8. Даны вершины треугольника: А(-10, -13), В(-2, 3) и С(2, 1). Вычислить длину перпендикуляра, опущенного из вершины В на медиану, проведенную из вершины С.
12.9. Установить, лежат ли точка Р(1, -3) и начало координат по одну или по разные стороны прямой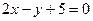 
.
12.10. Даны две смежные вершины квадрата А(2, 0) и В(-1, 4). Составить уравнение его сторон.
12.11. Составить геометрическое место точек, равноудаленных от параллельных прямых 
и 
.
12.12. Составить уравнение прямой, проходящей через точку А(2, 3) и отсекающей на координатных осях отрезки равной длины, считая каждый отрезок от начала координат.
12.13. Найти угол между двумя прямыми:
а)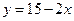 
и 
;
б) 
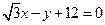и 
.
12.14. Найти уравнение прямой, проходящей через начало координат и образующей с прямой у = 2х - 4 угол 45°.
12.15. Дан треугольник с вершинами А(7,0), В(3,-4), С(2,3). Найти уравнения стороны АВ, высоты CD, биссектрисы BE, медианы CF.
Занятие № 13.
Кривые второго порядка.
13.1. Составить уравнение окружности, касающейся двух параллельных прямых: 
, 
, причем одной из них – в точке А(2, 1).
13.2. Составить уравнение окружности, касающейся осей координат, если центр окружности лежит в точке с координатами 
.
13.3. Дана окружность 
. Из ее точки А(2,0) проведены всевозможные хорды. Определить геометрическое место середин этих хорд.
13.4. Дан эллипс 
найти:
1) его полуоси,
2) фокусы,
3) эксцентриситет,
4) уравнение директрис.
13.5. Составить уравнение эллипса, фокусы которого лежат на оси абсцисс, симметрично относительно начала координат, зная, что
1) его полуоси равны 3 и 2;
2) его малая ось равна 24, а расстояние между фокусами 2с=10.
3) его большая ось равна 20, а расстояние между фокусами 2с=12,
4) его малая полуось равна 10, а эксцентриситет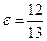 
,
5) его большая ось равна 20, а эксцентриситет 
.
6) расстояние между его директрисами равно 10 и расстояние между фокусами 2с=8,
7) его большая ось равна 8, а расстояние между директрисами равно 16,
8) его малая ось равна 4 расстояние между директрисами равно 10,
9) расстояние между его директрисами равно 16 и 
.
13.6. Найти острый угол между асимптотами гиперболы 
.
13.7. Составить уравнение гиперболы, фокусы которой расположены на оси абсцисс, симметрично относительно начала координат, зная, что
1) ее оси 2а=4 и 2b=6,
2) расстояние между фокусами 2с=16 и ось 2b=12,
3) расстояние между фокусами 2с=6 и эксцентриситет 
,
4) расстояние между директрисами равно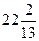 
и расстояние между фокусами 2с = 26;
5) расстояние между директрисами равно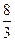 
и эксцентриситет ;
6) расстояние между директрисами равно 
, а уравнения асимптот имеют вид 
.
13.8. Составить уравнение параболы, вершина которой находится в начале координат, зная, что парабола расположена в правой полуплоскости симметрично относительно оси 
и ее параметр р=3.
13.9. Составить уравнение параболы, которая имеет фокус F (0,-3) и проходит через начало координат, зная, что ее осью служит ось 
.
13.10. Найти координаты фокуса параболы:
1) 
;
2) 
,
3) 
;
4) 
.
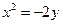13.11. Найти вершину, фокус, ось и директрису параболы 
.
Занятие № 14.