Обратная матрица. Вычисление обратной матрицы

Алгоритм нахождения обратной матрицы

1. Определяют, квадратная ли матрица. Если нет, то обратной матрицы для нее не существует.

2. Вычисление определителя матрицы A. Если он не равен нулю, продолжаем решение, иначе - обратной матрицы не существует.

3. Нахождение транспонированной матрицы A^T.

4. Определение алгебраических дополнений. Заменяют каждый элемент матрицы его алгебраическим дополнением.

5. Составление обратной матрицы из алгебраических дополнений: каждый элемент полученной матрицы делят на определитель исходной матрицы. Результирующая матрица является обратной для исходной матрицы.

6. Делают проверку: перемножают исходную и полученную матрицы. В результате должна получиться единичная матрица.

Решение систем линейных уравнений по формулам Крамера.

Система из двух уравнений с двумя неизвестными

решается с помощью формул Крамера:

, ,

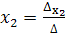где 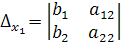и , .

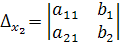При решении системы возможны три случая:

1. Определитель системы 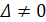. Тогда система имеет единственное решение, определяемое формулами Крамера.

2. Определитель системы 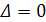. Если при этом хотя бы один из определителей и не равен нулю, то система не имеет решений.

3. Если , и 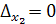, то одно из уравнений есть следствие другого, система сводится к одному уравнению с двумя неизвестными и имеет бесчисленное множество решений.

Пример. Решить систему уравнений .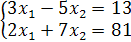

Решение. Вычислим определитель системы , и дополнительные определители ,

Система имеет единственное решение

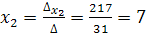, Ответ: .

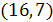Решение систем линейных уравнений методом Гаусса.

смысл метода: последовательно исключаем переменную за переменной, пока в одной из строк не будет однозначно определена переменная x_i. Идею можно проиллюстрировать на простом примере:
x₁ - x₂ = 3
-x₁ + 2x₂ = 1
=========== (складываем строки)
-x₂ + 2x₂= 3 + 1 = 4 или x₂ = 4
Откуда, x₁ = 7

Суть метода можно понять, проанализировав пример решения.
ПРИМЕР. Запишем систему в виде расширенной матрицы:

-1 -1

Далее умножаем 2-ую строку на (2) и добавляем к первой:

-1

Добавим 3-ую строку к 2-ой:

Умножим первую строчку на (3), 2-ую строку умножаем на (-1). Следующее действие: складываем первую и вторую строки:

Теперь исходную систему можно записать как:
x₃ = 51/17
x₂ = [27 - 7x₃]/3
x₁ = [14 - (2x₂ + 3x₃)]
Из 1-ой строки выражаем x₃: 51/17 = 3
Из 2-ой строки выражаем x₂: (27 - 7*3)/3 = 2
Из 3-ой строки выражаем x₁: (14 - 2*2 - 3*3) = 1

Матричное решение систем линейных уравнений.

В этой статье поговорим о матричном методе решения систем линейных алгебраических уравнений вида , которые в матричной форме записываются как 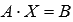, где - основная матрица системы, 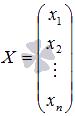- матрица-столбец неизвестных переменных, - матрица свободных членов.