Знаки тригонометрических функций
| sin α | cos α | tg α | ctg α | |
| 0< α <π/2 | + | + | + | + |
| π/2< α < π | + | – | – | – |
| π< α <3π/2 | – | – | + | + |
| 3π/2< α <2π | – | + | – | – |
Значения функций характерных углов
| радианы | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π | |
| градусы | 00 | 300 | 450 | 600 | 900 | 1800 | 2700 | 3600 |
| sin α | ½ | √2/2 | √3/2 | –1 | ||||
| cos α | √3/2 | √2/2 | ½ | –1 | ||||
| tg α | √3/3 | √3 | ∞ | ∞ | ||||
| ctg α | ∞ | √3 | √3/3 | ∞ | ∞ |
Формулы приведения. Чётность.
| аргумент | функция | sin | cos | tg | ctg |
| –α | –sinα | cosα | –tgα | –ctgα | |
| π/2 ± α | cosα | 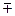 sinα sinα | 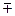 ctgα ctgα | 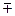 tgα tgα | |
| π ± α | 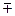 sinα sinα | –cosα | 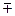 tgα tgα | 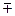 ctgα ctgα |
Основные соотношения
sin2α + cos2α = 1; tgα · ctgα = 1; tgα = sinα/cosα = 1/ctgα;
ctgα = cosα/sinα = 1/tgα; 1 + tg2α = 1/cos2α; 1 + ctg2α = 1/sin2α; secα = 1/cosα; cosecα = 1/sinα;
Периодичность
функции sinα и cosα имеют период 2π, а функции tgα и ctgα – период π.
sin(α + 2πn) = sinα, n 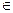 Z; cos(α + 2πn) = cosα, n
Z; cos(α + 2πn) = cosα, n 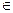 Z; tg(α + πn) = tgα, n
Z; tg(α + πn) = tgα, n 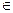 Z; ctg(α + πn) = ctgα, n
Z; ctg(α + πn) = ctgα, n 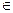 Z;
Z;
Формулы для суммы и разности аргументов.
sin(α ± β) = sinα · cosβ ± cosα · sinβ; cos(α ± β) = cosα · cosβ 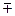 sinα · sinβ;
sinα · sinβ;
tg(α ± β) = (tgα ± tgβ) / (1 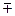 tgα · tgβ); ctg(α ± β) = (ctgα · ctgβ
tgα · tgβ); ctg(α ± β) = (ctgα · ctgβ 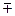 1) / (ctgβ ± ctgα);
1) / (ctgβ ± ctgα);
Функции двойных углов
sin2α = 2sinα · cosα; cos2α = cos2α – sin2α = 1–2sin2α = 2cos2α – 1;
tg2α = 2tgα / (1–tg2α); ctg2α = (ctg2α – 1) / 2ctgα;
Функции половинного угла
sin(α/2) = ± 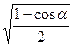 cos(α/2) = ±
cos(α/2) = ±  tg(α/2) = ±
tg(α/2) = ± 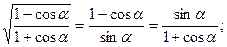
2sin2(α/2) = 1 – cosα; 2cos2(α/2) = 1 + cosα; sin2α = (1–cos2α) / 2
Функции полного угла
sinα = 2tg(α/2) / (1+ tg2(α/2)); cosα = (1–tg2(α/2)) / (1+tg2(α/2)); tgα = 2tg(α/2) / (1–tg2(α/2));
Функции тройного угла
sin3α = 3sinα – 4sin3α; cos3α = 4cos3α – 3cosα;
Произведения тригонометрических функций
sinα · cosβ = ½ · (sin(α + β) + sin(α – β)); cosα · cosβ = ½ · (cos(α + β) + cos(α – β));
sinα · sinβ = ½ · cos(α – β) – cos(α + β));
Сумма и разность тригонометрических функций
sinα + sinβ = 2 · sin((α + β)/2) · cos((α – β)/2); sinα – sinβ = 2 · sin((α – β)/2) · cos((α + β)/2);
cosα + cosβ = 2 · cos((α + β)/2) · cos((α – β)/2); cosα – cosβ = 2 · sin((α + β)/2) · sin((α – β)/2);
tgα ± tgβ = sin(α ± β) / (cosα · cosβ); cosα ± sinα =  ;
;
Тригонометрические уравнения
sinα = a, α = arcsin a + 2π·n, n 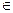 Z;
Z;
α = π – arcsin a + 2π·n, n 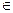 Z;
Z;
cosα = a, α = ± arccos a + 2π n, n 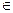 Z;
Z;
tgα = a, α = arctg a + π·n, n 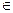 Z;
Z;
ctgα = a, α = arcctg a + π·n, n 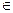 Z.
Z.
Частные случаи
sin x = ±1, x = ± π/2 + 2π, n 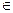 Z; sin x = 0, x = πn, n
Z; sin x = 0, x = πn, n 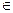 Z;
Z;
cos x = –1, x = π + 2πn, n 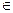 Z; cos x = 0, x = π/2 + πn, n
Z; cos x = 0, x = π/2 + πn, n 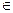 Z; cos x = 1, x = 2πn, n
Z; cos x = 1, x = 2πn, n 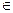 Z;
Z;
Обратные тригонометрические функции отрицательного аргумента
arcsin(–α) = –arcsinα; arccos(–α) = π – arccosα; arctg(–α) = –arctgα; arcctg(–α) = = π–arcctgα;
Таблица первообразных
| Функция. | Первообразная. |
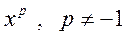 | 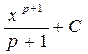 |
 | 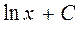 |
| ex | ex+C |
| sin x | – cosx +C |
| cos x | sinx + C |
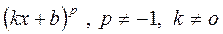 | 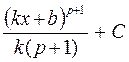 |
 |  |
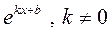 |  |
sin(kx + b), 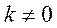 | 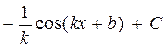 |
cos(kx+b), 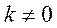 | 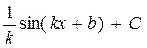 |
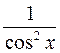 | tgx + C |
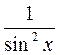 | −ctgx + C |
ГЕОМЕТРИЯ
МЕТОД КООРДИНАТ
Пусть на (i, j, k) заданы 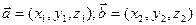 , тогда операции над ними будут равны:
, тогда операции над ними будут равны:

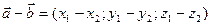 ;
; 


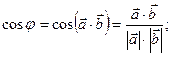
 Пусть A ( x1; y1; z1); B (x2; y2; z2); тогда:
Пусть A ( x1; y1; z1); B (x2; y2; z2); тогда:
вектор 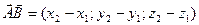 ; модуль вектора
; модуль вектора 
ТРЕУГОЛЬНИК
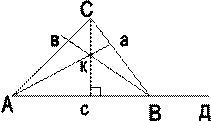 внешний угол СВД =
внешний угол СВД = 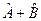 ; К – точка пересечения высот (ортоцентр треугольника). ha, hb, hc – высоты треугольника на соответствующие стороны.
; К – точка пересечения высот (ортоцентр треугольника). ha, hb, hc – высоты треугольника на соответствующие стороны.

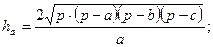 где полупериметр
где полупериметр 
 .
.
 М – точка пересечения медиан треугольника (центр тяжести).
М – точка пересечения медиан треугольника (центр тяжести).
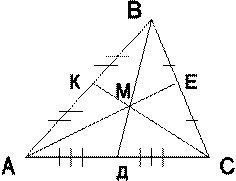 ma, mb, mc – медианы на соответствующие стороны. МВ:МД=МА:МЕ=МС:МК=2/1
ma, mb, mc – медианы на соответствующие стороны. МВ:МД=МА:МЕ=МС:МК=2/1

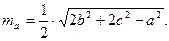
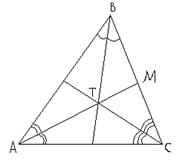
 Т – точка пересечения биссектрис треугольника (центр вписанной окружности). La, Lb, Lc – биссектрисы соответствующих углов. ВМ:МС = АВ:АС
Т – точка пересечения биссектрис треугольника (центр вписанной окружности). La, Lb, Lc – биссектрисы соответствующих углов. ВМ:МС = АВ:АС
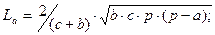

|

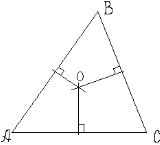

 где SΔ – площадь треугольника; p – периметр треугольника; hc –
где SΔ – площадь треугольника; p – периметр треугольника; hc –
высота опущенная на соответствующую сторону с. На всех 4–х нарисованных треугольниках стороны одинаково обозначены, просто на 1–м они обозначены, а на остальных они опущены для упрощения рисунка. И вообще подразумевается, что все 4 треугольника абсолютно одинаковые.
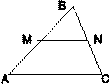 MN – средняя линяя треугольника. MN=0.5AC; MN║AC.
MN – средняя линяя треугольника. MN=0.5AC; MN║AC.
ТЕОРЕМА СИНУСОВ

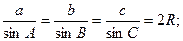 где R – радиус описанной окружности.
где R – радиус описанной окружности.

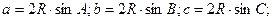
 ТЕОРЕМА КОСИНУСОВ
ТЕОРЕМА КОСИНУСОВ

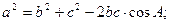
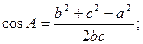

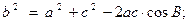


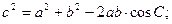

ПЛОЩАДЬ ТРЕУГОЛЬНИКА

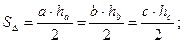 где
где  – длины сторон треугольника, а
– длины сторон треугольника, а  – высоты, опущенные на соответствующие стороны.
– высоты, опущенные на соответствующие стороны. 
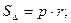
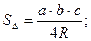
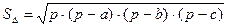 – формула Герона.
– формула Герона.
