Тейлор (1685-1731) – английский математик

Теорема Тейлора. 1) Пусть функция f(x) имеет в точке х = а и некоторой ее окрестности производные порядка до (n+1) включительно.{ Т.е. и все предыдущие до порядка n функции и их производные непрерывны и дифференцируемы в этой окрестности}.

2) Пусть х- любое значение из этой окрестности, но х ¹ а.

Тогда между точками х и а найдется такая точка e, что справедлива формула:

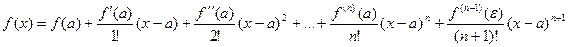
- это выражение называется формулой Тейлора, а выражение:

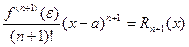
называется остаточным членом в форме Лагранжа.

Доказательство. Представим функцию f(x) в виде некоторого многочлена P_n(x), значение которого в точке х = а равно значению функции f(x), а значения его производных равно значениям соответствующих производных функции в точке х = а.

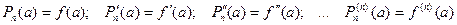(1)

Многочлен P_n(x) будет близок к функции f(x). Чем больше значение n, тем ближе значения многочлена к значениям функции, тем точнее он повторяет функцию.

Представим этот многочлен с неопределенными пока коэффициентами:

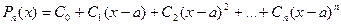(2)

Для нахождения неопределенных коэффициентов вычисляем производные многочлена в точке х = а и составляем систему уравнений:

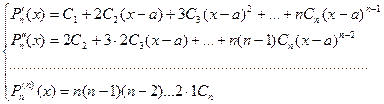(3)

Решение этой системы при х = а не вызывает затруднений, получаем:

…………………….

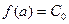
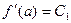
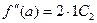
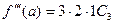
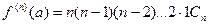
Подставляя полученные значения C_i в формулу (2), получаем:

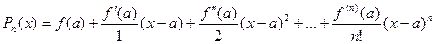
Как было замечено выше, многочлен не точно совпадает с функцией f(x), т.е. отличается от нее на некоторую величину. Обозначим эту величину R_n+1(x). Тогда:

f(x) = P_n(x) + R_n+1(x)

Теорема доказана.

Рассмотрим подробнее величину R_n+1(x).

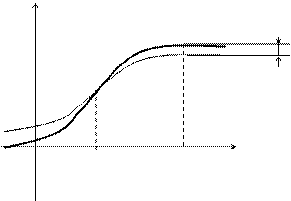
y Как видно на рисунке, в

точке х = а значение мно-

f(x) R_n+1(x) гочлена в точности совпа-

дает со значением функции.

P_n(x) Однако, при удалении от точ-

ки х = а расхождение значе- ний увеличивается.

0 a x x

Иногда используется другая запись для R_n+1(x). Т.к. точка eÎ(a, x), то найдется такое число q из интервала 0 < q < 1, что e = a + q(x – a).

Тогда можно записать:

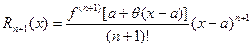
Тогда, если принять a = x₀, x – a = Dx, x = x₀ + Dx, формулу Тейлора можно записать в виде:

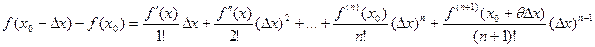
где 0 < q < 1

Если принять n =0, получим: f(x₀ + Dx) – f(x₀) = f¢(x₀ + qDx)×Dx – это выражение называется формулой Лагранжа. (Жозеф Луи Лагранж (1736-1813) французский математик и механик).

Формула Тейлора имеет огромное значение для различных математических преобразований. С ее помощью можно находить значения различных функций, интегрировать, решать дифференциальные уравнения и т.д.

При рассмотрении степенных рядов будет более подробно описаны некоторые особенности и условия разложения функции по формуле Тейлора.

Формула Маклорена.

Колин Маклорен (1698-1746) шотландский математик.

Формулой Маклоренаназывается формула Тейлора при а = 0:

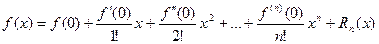
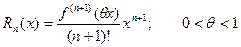
Мы получили так называемую формулу Маклорена с остаточным членом в форме Лагранжа.

Следует отметить, что при разложении функции в ряд применение формулы Маклорена предпочтительнее, чем применение непосредственно формулы Тейлора, т.к. вычисление значений производных в нуле проще, чем в какой- либо другой точке, естественно, при условии, что эти производные существуют.

Однако, выбор числа а очень важен для практического использования. Дело в том, что при вычислении значения функции в точке, расположенной относительно близко к точке а, значение, полученное по формуле Тейлора, даже при ограничении тремя – четырьмя первыми слагаемыми, совпадает с точным значением функции практически абсолютно. При удалении же рассматриваемой точки от точки а для получения точного значения надо брать все большее количество слагаемых формулы Тейлора, что неудобно.

Т.е. чем больше по модулю значение разности (х – а) тем более точное значение функции отличается от найденного по формуле Тейлора.

Кроме того, можно показать, что остаточный член R_n+1(x) является бесконечно малой функцией при х®а, причем долее высокого порядка, чем (х – а)^m, т.е.

.

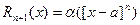Таким образом, ряд Маклорена можно считать частным случаем ряда Тейлора.

Представление некоторых элементарных функций

по формуле Тейлора.

Применение формулы Тейлора для разложения функций в степенной ряд широко используется и имеет огромное значение при проведении различных математических расчетов. Непосредственное вычисление интегралов некоторых функций может быть сопряжено со значительными трудностями, а замена функции степенным рядом позволяет значительно упростить задачу. Нахождение значений тригонометрических, обратных тригонометрических, логарифмических функций также может быть сведено к нахождению значений соответствующих многочленов.

Если при разложении в ряд взять достаточное количество слагаемых, то значение функции может быть найдено с любой наперед заданной точностью. Практически можно сказать, что для нахождения значения любой функции с разумной степенью точности (предполагается, что точность, превышающая 10 – 20 знаков после десятичной точки, необходима очень редко) достаточно 4-10 членов разложения в ряд.

Применение принципа разложения в ряд позволяет производить вычисления на ЭВМ в режиме реального времени, что немаловажно при решении конкретных технических задач.

Функция f(x) = e^x.

Находим: f(x) = e^x, f(0) = 1

f¢(x) = e^x, f¢(0) = 1

……………………

f⁽ⁿ⁾(x) = e^x, f⁽ⁿ⁾(0) = 1

Тогда: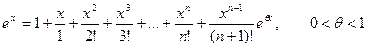

Пример: Найдем значение числа е.

В полученной выше формуле положим х = 1.

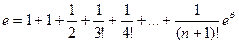
Для 8 членов разложения: e = 2,71827876984127003

Для 10 членов разложения: e = 2,71828180114638451

Для 100 членов разложения: e = 2,71828182845904553

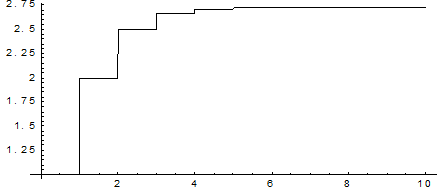
На графике показаны значения числа е с точностью в зависимости от числа членов разложения в ряд Тейлора.

Как видно, для достижения точности, достаточной для решения большинства практических задач, можно ограничиться 6-7 – ю членами ряда.

Функция f(x) = sinx.

Получаем f(x) = sinx; f(0) = 0

f¢(x) = cosx = sin( x + p/2); f¢(0) = 1;

f¢¢(x) = -sinx = sin(x + 2p/2); f¢¢(0) = 0;

f¢¢¢(x) = -cosx = sin(x + 3p/2); f¢¢¢(0)=-1;

…………………………………………

f⁽ⁿ⁾(x) = sin(x + pn/2); f⁽ⁿ⁾(0) = sin(pn/2);

f⁽ⁿ⁺¹⁾(x) = sin(x + (n + 1)p/2); f⁽ⁿ⁺¹⁾(e) = sin(e + (n + 1)p/2);

Итого: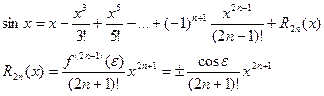

Функция f(x) = cosx.

Для функции cosx, применив аналогичные преобразования, получим:

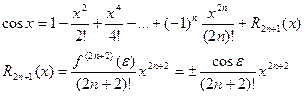
Функция f(x) = (1 + x)^a.

(a - действительное число)

…………………………………………………..

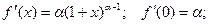
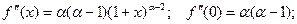
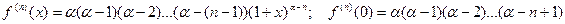
Тогда:

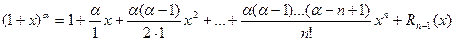
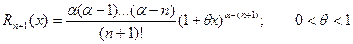
Если в полученной формуле принять a = n, где n- натуральное число и f⁽ⁿ⁺¹⁾(x)=0, то R_n+1 = 0, тогда

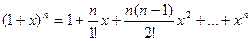
Получилась формула, известная как бином Ньютона.

Пример: Применить полученную формулу для нахождения синуса любого угла с любой степенью точности.

На приведенных ниже графиках представлено сравнение точного значения функции и значения разложения в ряд Тейлора при различном количестве членов разложения.

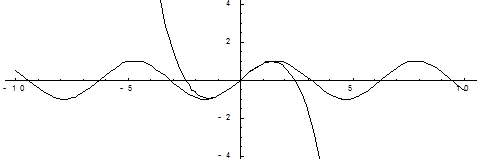
Рис. 1. Два члена разложения

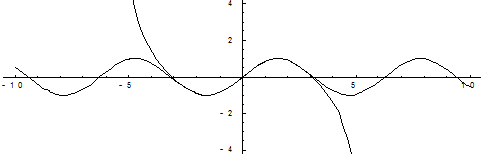
Рис. 2. Четыре члена разложения

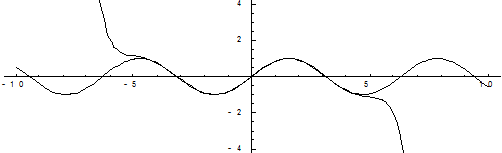
Рис. 3. Шесть членов разложения

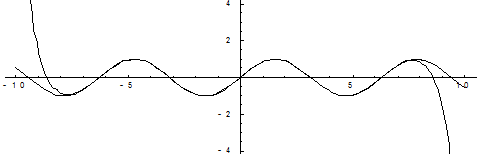
Рис. 4. Десять членов разложения

Чтобы получить наиболее точное значение функции при наименьшем количестве членов разложения надо в формуле Тейлора в качестве параметра а выбрать такое число, которое достаточно близко к значению х, и значение функции от этого числа легко вычисляется.

Для примера вычислим значение sin20⁰.

Предварительно переведем угол 20⁰ в радианы: 20⁰ = p/9.

Применим разложение в ряд Тейлора, ограничившись тремя первыми членами разложения:

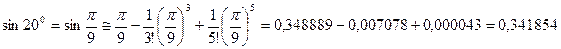
В четырехзначных таблицах Брадиса для синуса этого угла указано значение 0,3420.

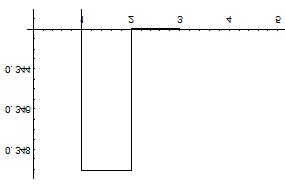
На графике показано изменение значений разложения в ряд Тейлора в зависимости от количества членов разложения. Как видно, если ограничиться тремя членами разложения, то достигается точность до 0,0002.

Выше говорилось, что при х®0 функция sinx является бесконечно малой и может при вычислении быть заменена на эквивалентную ей бесконечно малую функцию х. Теперь видно, что при х, близких к нулю, можно практически без потери в точности ограничиться первым членом разложения, т.е. sinx @ x.

Пример: Вычислить sin28⁰13¢15¢¢.

Для того, чтобы представить заданный угол в радианах, воспользуемся соотношениями:

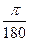1⁰ = ; 28⁰ ;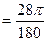

1¢ ; ;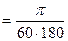

; ;

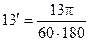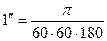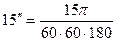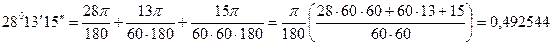рад

Если при разложении по формуле Тейлора ограничиться тремя первыми членами, получим: sinx = .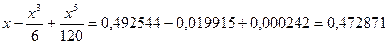

Сравнивая полученный результат с более точным значением синуса этого угла,

sin 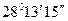= 0,472869017612759812,

видим, что даже при ограничении всего тремя членами разложения, точность составила 0,000002, что более чем достаточно для большинства практических технических задач.

Функция f(x) = ln(1 + x).

Получаем: f(x) = ln(1 + x); f(0) = 0;

f¢(x) = ;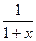

………………………………………

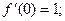
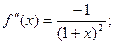
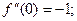
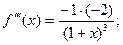
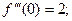
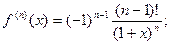
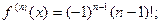
Итого: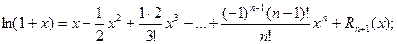

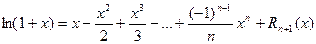
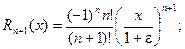
Полученная формула позволяет находить значения любых логарифмов (не только натуральных) с любой степенью точности. Ниже представлен пример вычисления натурального логарифма ln1,5. Сначала получено точное значение, затем – расчет по полученной выше формуле, ограничившись пятью членами разложения. Точность достигает 0,0003.

ln1,5 = 0,405465108108164381

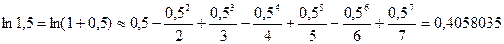
Разложение различных функций по формулам Тейлора и Маклорена приводится в специальных таблицах, однако, формула Тейлора настолько удобна, что для подавляющего большинства функций разложение может быть легко найдено непосредственно.

Ниже будут рассмотрены различные применения формулы Тейлора не только к приближенным представлениям функций, но и к решению дифференциальных уравнений и к вычислению интегралов.

Применение дифференциала к приближенным вычислениям.

Дифференциал функции y = f(x) зависит от Dх и является главной частью приращения Dх.

Также можно воспользоваться формулой

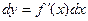
Тогда абсолютная погрешность

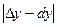
Относительная погрешность

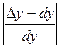
Более подробно применение дифференциала к приближенным вычислениям будет описано ниже.

При использовании компьютерной версии “Курса высшей математики” возможно запустить программу, которая производит разложение любой функции в ряды Тейлора и Маклорена, а также вычисляет значение функции в заданной точке, выводит погрешность вычислений.

Для запуска программы дважды щелкните на значке

Примечание: Для запуска программы необходимо чтобы на компьютере была установлена программа Maple (Ó Waterloo Maple Inc.) любой версии, начиная с MapleV Release 4.

Теоремы о среднем.

Теорема Ролля.

(Ролль (1652-1719)- французский математик)

Если функция f(x) непрерывна на отрезке [a, b], дифференцируема на интервале (а, b) и значения функции на концах отрезка равны f(a) = f(b), то на интервале (а, b) существует точка e, a < e < b, в которой производная функция f(x) равная нулю,

f¢(e) = 0.

Геометрический смысл теоремы Ролля состоит в том, что при выполнении условий теоремы на интервале (a, b) существует точка e такая, что в соответствующей точке кривой y = f(x) касательная параллельна оси Ох. Таких точек на интервале может быть и несколько, но теорема утверждает существование по крайней мере одной такой точки.

Доказательство. По свойству функций, непрерывных на отрезке функция f(x) на отрезке [a, b] принимает наибольшее и наименьшее значения. Обозначим эти значения М и m соответственно. Возможны два различных случая М = m и M ¹ m.

Пусть M = m. Тогда функция f(x) на отрезке [a, b] сохраняет постоянное значение и в любой точке интервала ее производная равна нулю. В этом случае за e можно принять любую точку интервала.

Пусть М = m. Так значения на концах отрезка равны, то хотя бы одно из значений М или m функция принимает внутри отрезка [a, b]. Обозначим e, a < e < b точку, в которой f(e) = M. Так как М- наибольшее значение функции, то для любого Dх ( будем считать, что точка e + Dх находится внутри рассматриваемого интервала) верно неравенство:

Df(e) = f(e + Dx) – f(e) £ 0

При этом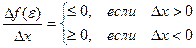

Но так как по условию производная в точке e существует, то существует и предел .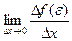

Т.к. 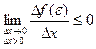и 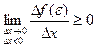, то можно сделать вывод:

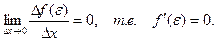
Теорема доказана.

Теорема Ролля имеет несколько следствий:

1) Если функция f(x) на отрезке [a, b] удовлетворяет теореме Ролля, причем

f(a) = f(b) = 0, то существует по крайней мере одна точка e, a < e < b, такая, что f¢(e) = 0. Т.е. между двумя нулями функции найдется хотя бы одна точка, в которой производная функции равна нулю.

2) Если на рассматриваемом интервале (а, b) функция f(x) имеет производную (n-1)- го порядка и n раз обращается в нуль, то существует по крайней мере одна точка интервала, в котором производная (n – 1) – го порядка равна нулю.

Теорема Лагранжа.

(Жозеф Луи Лагранж (1736-1813) французский математик)

Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема на интервале (а, b), то на этом интервале найдется по крайней мере одна точка e

a < e < b, такая, что .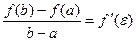

Это означает, что если на некотором промежутке выполняются условия теоремы, то отношение приращения функции к приращению аргумента на этом отрезке равно значению производной в некоторой промежуточной точке.

Рассмотренная выше теорема Ролля является частным случаем теоремы Лагранжа.

Отношение 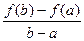равно угловому коэффициенту секущей АВ.

у

В

А

0 а e b x

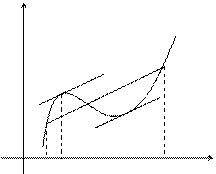
Если функция f(x) удовлетворяет условиям теоремы, то на интервале (а, b) существует точка e такая, что в соответствующей точке кривой y = f(x) касательная параллельна секущей, соединяющей точки А и В. Таких точек может быть и несколько, но одна существует точно.

Доказательство. Рассмотрим некоторую вспомогательную функцию

F(x) = f(x) – y_{сек АВ}

Уравнение секущей АВ можно записать в виде:

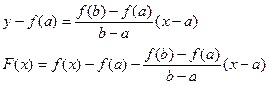
Функция F(x) удовлетворяет теореме Ролля. Действительно, она непрерывна на отрезке [a, b] и дифференцируема на интервале (а, b). По теореме Ролля существует хотя бы одна точка e, a < e < b, такая что F¢(e) = 0.

Т.к. 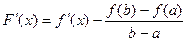, то 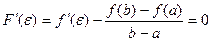, следовательно

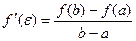
Теорема доказана.