Приведение двух квадратичных форм к каноническому виду

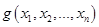Рассмотрим две вещественные квадратичные формы и . Можно ли заданные формы единым преобразованием привести к каноническому виду? Эту задачу помогают решить результаты, относящиеся к линейным операторам. Мы рассмотрим случай, когда одна из этих квадратичных форм, например 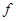, является положительно определенной. Тогда выполняем сначала преобразование 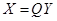, которое приводит форму 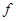к нормальному виду (сумме квадратов переменных). При этом форма перейдет в новую форму от переменных . На следующем шаге выполняется ортогональное преобразование 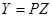, которое приводит форму к каноническому виду. Квадратичная форма 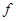при этом не изменится, так как ее матрица является единичной, а .

Итак, результирующим преобразованием, которое приведет обе квадратичные формы к каноническому виду, причем положительно определенную представит в виде суммы квадратов, будет .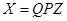

Задача 5.1.Для заданной пары квадратичных форм найти невырожденное линейное преобразование, которое приводит эти формы к каноническому виду.

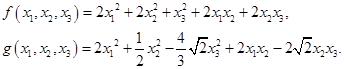
Решение.

Перепишем формы 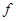и в виде и , где 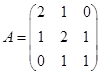, 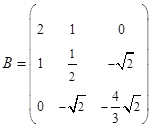- матрицы соответствующих квадратичных форм.

Так как 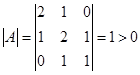, то согласно критерию Сильвестра, форма 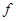является положительно определенной. Поэтому по ней можно восстановить соответствующую билинейную форму и ввести в скалярное произведение .

Оно удовлетворяет всем аксиомам скалярного произведения (положительная определенность формы необходима для выполнения аксиомы 4 , а именно ).

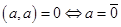Рассмотрим стандартный базис в : .

Используя введенное скалярное произведение, ортогонализируем его:

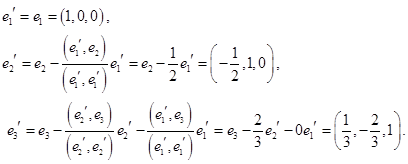
Нормируем вектора и получаем ОНБ в , в котором билинейная форма (следовательно, и квадратичная форма 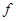) будет иметь единичную матрицу.

Матрица перехода от старого базиса к новому задает матрицу 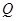невырожденного преобразования переменных 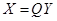квадратичных форм 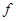и .

.

Действительно,

.

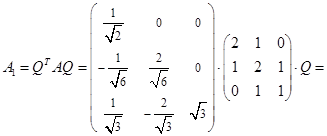
Аналогично,

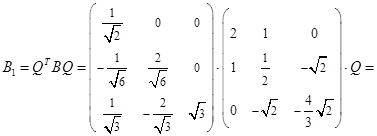
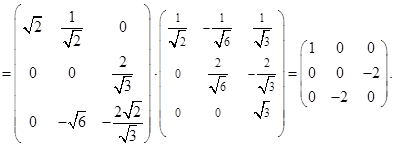
Далее используем метод приведения квадратичной формы к главным осям.

Характеристический многочлен

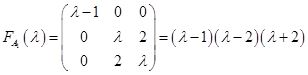имеет три корня 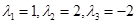, которым соответствуют следующие собственные вектора: 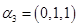. Они являются попарно ортогональными, так как соответствуют разным собственным значениям, и образуют собственный ортогональный базис. Осталось его пронормировать:

.

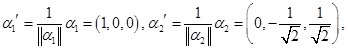
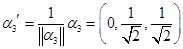Теперь составляем ортогональную матрицу, столбцами которой являются векторы , ,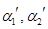

.

Тогда матрица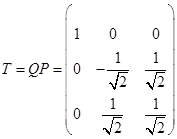

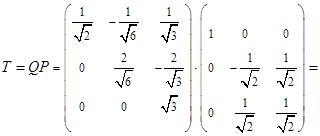
и будет искомой матрицей невырожденного линейного преобразования переменных

приводящего формы 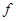и к каноническому виду

,

.

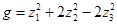Задача решена.

Список литературы

1. Завало С.Т., Костарчук В.Н., Хацет Б.И.Алгебра и теория чисел, ч.1. –К.: Вища школа, 1980.

2. Кострикин А. И. Введение в алгебру. - М.: Наука, 1977 .

3.Курош А.Г. Курс высшей алгебры. – М.: Наука, 1975.

4. Проскуряков. Сборник задач по линейной алгебре.М., Наука, 1974.