Методические указания по выполнению контрольной работы

Колледж ВятГУ

МАТЕМАТИКА

Методические указания для обучающихся заочной формы обучения

по специальности 38.02.06 Финансы

среднего профессионального образования

(по программе базовой подготовки)

Киров

РАССМОТРЕНО И ОДОБРЕНО к применению на заседании ПЦК специальности 38.02.06 Финансы, протокол №1 от 31.08.2015 г. председатель ПЦК _________/_______________

Разработана на основе федерального государственного образовательного стандарта по специальности среднего профессионального образования 38.02.06 Финансы Заместитель директора по УМР ______________ Г.П.Логинова 01.09.2015 г.

Организация разработчик: колледж ВятГУ

Разработчик: Балдина Юлия Николаевна, преподаватель колледжа ВятГУ

Аннотация

Пособие предназначено для оказания помощи студентам заочного отделения при выполнении домашней контрольной работы по математике или по элементам высшей математики.

Содержание

Теория пределов

Изучить по учебной литературе вопросы:

1. Определение предела функции.

2. Свойства пределов функций.

3. Вычисление пределов функций при наличии неопределенности типа 0/0.

4. Вычисление пределов функций, являющихся неопределенностями типа ¥/¥.

5. Понятие разрыва функции. Типы разрывов.

6. Асимптоты графиков функций, их виды и уравнения.

7. Первый и второй замечательные пределы.

Функция одной переменной

Примеры решения задач

1. Вычислить пределы функций:

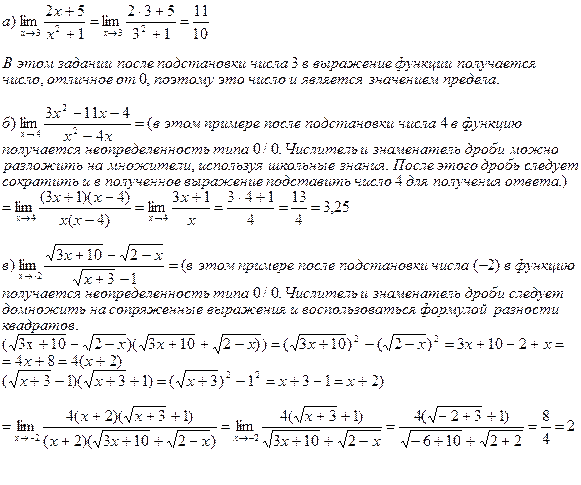
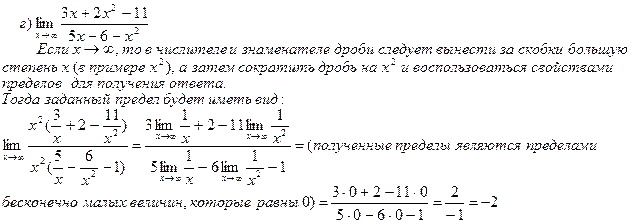
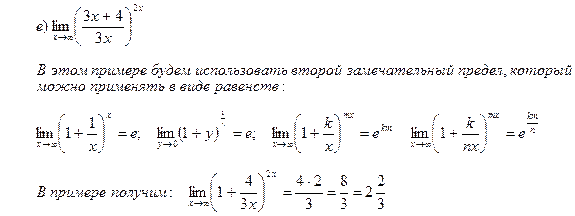
2. Составить уравнения асимптот к графику функции:

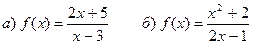
Решение

а) Графики функций могут иметь асимптоты трех видов: горизонтальные, вертикальные и наклонные.

Для определения горизонтальной асимптоты следует вычислить предел функции при условии, что х®¥. Если такой предел существует, то график функции имеет горизонтальную асимптоту.

В примере 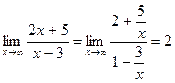График функции имеет горизонтальную асимптоту с уравнением у=2.

Для определения вертикальной асимптоты следует определить значения, при которых функция не существует и найти левые и правые пределы функции. Если хотя бы один из пределов бесконечен, то имеется вертикальная асимптота.

В примере функция не существует при х=3.

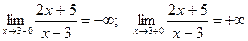Так как оба предела бесконечны, то имеется

вертикальная асимптота с уравнением х=3.

Для определения наклонной асимптоты с уравнением y=kx +b находят

Если первый предел не существует или равен 0, то нет наклонной асимптоты.

В примере

Так как k=0, то наклонной асимптоты не имеется.

б)

Выполним последовательно значения пределов:

График функции не имеет горизонтальной асимптоты.

Функция не существует при х=0,5

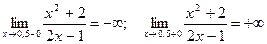График функции имеет вертикальную асимптоту

с уравнением х=0,5

Вычислим 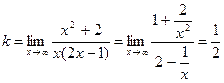График функции имеет наклонную асимптоту.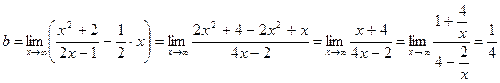

Наклонная асимптота имеет уравнение у=0,5х + 0,25

3. Исследовать функцию на четность.

Алгоритм исследования функции у = f(х) на четность

1. Установить, симметрична ли область определения функции. Если нет, то объявить, что функция не является ни четной, ни нечетной. Если да, то переходить ко второму шагу алгоритма

2. Найти f(-х).

3. Сравнить f (x)= f (-x)

а) если f(-х) = f(х), то функция — четная,

б) если f(-х) = -f(х), то функция — нечетная;

в) если хотя бы в одной точке х є Х выполняется соотношение f(-х) = f(х) и хотя бы в одной точке х є X выполняется соотношение f(-х) = -f(х), то функция не является ни четной, ни нечетной.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ

Контрольная работа выполняется по вариантам:

Буква фамилии	Варианты
А-Д
Е-К
Л-О
П-У
Ф-Я

Требования к оформлению:

1. Оформление каждой задачи с нового листа.

2. Должна быть приведена формулировка теоремы или формулы, которую вы используете, с обоснованием, почему именно эта теорема применяется.

3. Оформление задачи завершается выписыванием ответа.

4. В конце работы привести список использованной литературы.