Числовые последовательности
Числовая последовательность представляет собой некоторое множество чисел, каждому из которых присвоен определенный номер. Примерами последовательностей могут служить: последовательность всех членов арифметической и геометрической прогрессий; последовательность приближенных значений числа 
, т.е. 
, 
, 
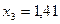, и т. д., последовательность периметров правильных n–угольников, вписанных в данную окружность и т.д.
Определение
Если каждому числу n из натурального ряда чисел 1,2,3, …, n, …, поставлено в соответствие вещественное число 
, то множество вещественных чисел
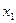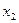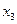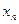 ,  ,  ,…,  ,…,… | (4.1.1) |
называется числовой последовательностью или просто последовательностью.
Числа 
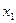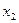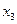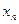, , ,…, будем называть элементами или членами последовательности (4.1.1), символ – общим элементом или членом последовательности, а число n – его номером. Сокращенно последовательность (4.1.1) будем обозначать символом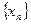 
Например, символ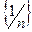 
обозначает последовательность чисел 
.
Геометрически последовательность можно изобразить на числовой оси в виде последовательности точек, координаты которых равны соответствующим членам последовательности.
Над числовыми последовательностями можно производить все арифметические операции, определяемые ниже.
Пусть даны последовательност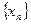и и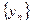 
. Тогда
1. Суммой (разностью) последовательносте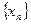й и 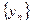назовем последовательность 
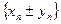с элементами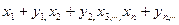 
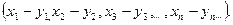
2. Произведением последовательности {xn} на число m назовем последовательность 
с элементами 
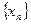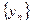3. Произведением последовательностей и назовем последовательность 
с элементами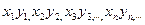 
4. Частным последовательносте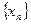й и 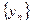назовем последовательность 
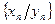с элементами 
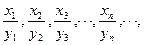, если все члены последовательности 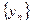отличны от нуля.
Ограниченные и неограниченные последовательности
Определение
Последовательность называется ограниченной сверху (снизу), если существует такое число M (число m), что любой элемент 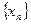этой последовательности удовлетворяет неравенству 
.
Определение
Последовательность 
называется ограниченной, если она ограниченна сверху и снизу, т.е. существуют такие числа mи M, что любой элемент этой последовательности удовлетворяет неравенству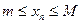 
.
Пусть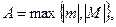 
, тогда условие ограниченности последовательности можно записать в форме 
.
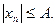Определение
Последовательность называется неограниченной, если для любого положительного числа A существует элемент 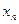этой последовательности, удовлетворяющий неравенству 
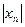>A, (т.е. либо 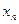>A, либо 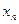<–A).
Из выше перечисленных определений следует, что все элементы ограниченной сверху последовательности принадлежат промежутку (– ¥, M); а ограниченной снизу – лежат в промежутке (m, + ¥). Все элементы ограниченной последовательности принадлежат отрезку [m, M].
Пример
1. Последовательность 
является ограниченной.
2. Последовательность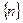 
является неограниченной сверху, но ограниченной снизу.
3. Последовательность 
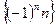является неограниченной.
Бесконечно большие и бесконечно малые последовательности
Определение
Последовательность называется бесконечно большой, если для любого положительного числа A существует такой номер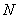 
, что для всех элементов последовательности с номерами 
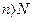выполняется неравенство 
.
Определение
Последовательность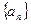 
называется бесконечно малой, если для любого положительного числа e существует такой номер 
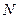, что для всех элементов последовательности с номерами 
выполняется неравенство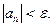 
Теперь докажем теорему, устанавливающую связь между бесконечно малыми и бесконечно большими последовательностями.
Теорема
Если 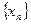– бесконечно большая последовательность и все ее члены отличны от нуля, то последовательность 
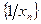бесконечно малая. Если все элементы бесконечно малой последовательности 
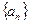отличны от нуля, то последовательность 
бесконечно большая.
Основные свойства бесконечно малых последовательностей
Теорема
Сумма и разность двух бесконечно малых последовательностей являются бесконечно малыми последовательностями.
Следствие
Алгебраическая сумма любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.
Теорема
Произведение двух бесконечно малых последовательностей есть бесконечно малая последовательность.
Следствие
Произведение конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.
Теорема
Произведение бесконечно малой последовательности на ограниченную последовательность является бесконечно малой последовательностью.
Следствие
Произведение бесконечно малой последовательности на постоянное число является бесконечно малой последовательностью.
4.2. Сходящиеся последовательности. Понятие предела
сходящейся последовательности
Определение
Число a называется пределом последовательности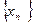 
, если для любого положительного числа e существует такой номер N, что при всех n>N выполняется неравенство
 | (4.2.1) |
Последовательность, имеющая предел, называется сходящейся. Если предел последовательности равен числу a, это записывается так: 
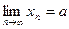, или 
при 
.
Последовательность, не имеющая предела, называется расходящейся.
Замечание 1
Пусть последовательность 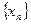имеет своим пределом число а. Тогда последовательность 
есть бесконечно малая, так как для любого 
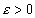существует такой номер N, что при выполняется неравенство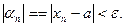 
Следовательно, любой элемент 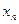сходящейся последовательности, имеющей предел а, можно представить в виде:
 | (4.2.2) |
где 
– элемент бесконечно малой последовательности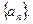 
.
Определение
Интервал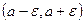 
называют e–окрестностью точки а.
Определение
Последовательность 
называется сходящейся, если существует такое число a, что в любой его e–окрестности находятся все элементы этой последовательности, начиная с некоторого номера, зависящего от e.
Интересно дать геометрическую интерпретацию этого определения. Поскольку последовательность определяет собой бесконечное множество чисел, то, если она сходится, в любой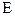 
–окрестности остается конечное число элементов. Поэтому предел последовательности часто называют точкой сгущения.
Замечание 2
Бесконечно большая последовательность не имеет предела. В этом случае говорят, что она имеет бесконечный предел: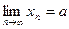
Замечание 3
Очевидно, что всякая бесконечно малая последовательность сходится и имеет своим пределом число a=0.
Приведем примеры сходящихся и расходящихся последовательностей. Покажем, используя определение предела последовательности, что 
Возьмем любое число 
. Так как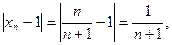 
то для удовлетворения неравенству (9.1.1) достаточно решить неравенство 
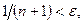откуда получаем 
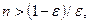
неравенство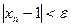 
будет выполняться при всех n>N, где 
.
Последовательность 
или –1, 1, –1, 1, … не имеет предела. Действительно, какое бы число мы ни предложили в качестве предела, 1 или –1, при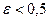 
неравенство (4.2.2), определяющее предел последовательности, не удовлетворяется: вне 
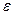– окрестности этих чисел остается бесконечное число элементов 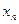: все элементы с нечетными номерами равны –1, элементы с четными номерами равны 1.
Основные свойства сходящихся последовательностей
Теорема
Если все элементы бесконечно малой последовательности 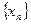равны одному и тому же числу с, то 
.
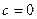Теорема
Сходящаяся последовательность имеет только один предел.
Теорема
Сходящаяся последовательность ограничена.
Замечание
Ограниченная последовательность может и не быть сходящейся. Так, последовательность 
, рассмотренная в примере 2, ограничена, но не имеет предела.
Теорема
Сумма (разность) сходящихся последовательносте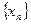й и 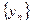есть сходящаяся последовательность, предел которой равен сумме (разности) пределов последовательносте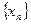й и .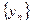
Теорема
Произведение сходящихся последовательностей и 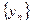есть сходящаяся последовательность, предел которой равен произведению пределов последовательносте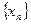й и .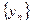
Теорема
Частное двух сходящихся последовательносте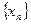й и 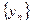при условии, что предел последовательности 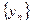отличен от нуля, есть сходящаяся последовательность, предел которой равен частному пределов последовательносте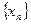й и 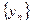.