Бұрыштық модуляция кезіндегі спектр.

Гармоникалық бұрыштық модуляция кезіндегі тербеліс спектрінің бастапқы жағдайы (1) өрнекпен анықталады. Қысқаша түрде φ₀=0 деп алып және (1) өрнегін былай жазамыз.

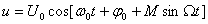. (1)

. (2)

Өрнек жиілігі ω₀ болатын 2 квадраттық тербелістің қосындысын береді (2), оның ішінде әрқайсысы амплитуда бойынша Ω жиілікпен модуляцияланған. Негізінен бұрыштық модуляция таржолақты (М<0,5 рад) және кең жолақты (M>0,5рад) болып бөлінеді. Байланыс техникасында кеңжолақты М>>1 болатын ЖМ кең қолданылады. Таржолақты бұрыштық модуляцияның спектрін анықтаудан бастайық. M << l десек, онда

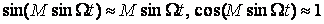, (3)

ал сондықтан

. (4)

Осылайша, таржолақты сигналдардың бұрыштық модуляциясының спектрі қарапайым АМ тербелісінің спектріне ұқсас, суретте көрсетілгендей.Ол тасушы жиілік ω₀ және 2 бүйір жиілігінен ω₀+Ω және ω₀−Ω-дан тұрады. Бүйірлік жиіліктердің амплитудасын анықтайтын бұл жердегі параметр ол модуляция индексі М болып табылады.

Таржолақты бұрыштық модуляцияның спектрінің ені, АМ кезіндегі сияқты. Ол модуляцияның екі еселенген жиілігіне тең. Спектрлердің ұқсастығына қарамастан, қарастырылып жақан тербеліс АМ тербелістен ерекшеленеді, ал ол таңбалардың арасындағы айырмашылық әсерінен болатын (яғни фаза бойынша 180 ығысу) төменгі бүйірлік жиілік құрамы (3) және (4) өрнектерінде. Бұл АМ тербелістің ФМ тербелісіне бүйірлік жиіліктердің біреуінің фаза бойынша ығысуы арқылы түрлендіруіне мүмкіндік береді. Кең жолақты бұрыштық модуляция кезінде және және өрнектері дұрыс емес. Тербеліс спектрін (2) өрнек бойынша анықтауға тура келеді. 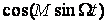және өрнектері жиіліктің периодты функциялары болып табылады, сондықтанда Фурье қатарына жіктеуге болады. Бұл функциялардың біріншісі-жұп, екіншісі-тақ

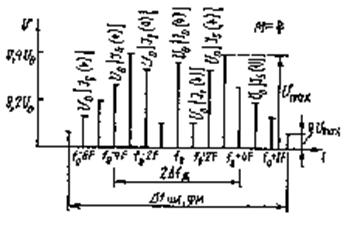
1 Сурет

Осылайша ЖМ және ФМ тербелістерінің спектрі, гармоникалық сигналмен модуляцияланған, дискреттік болып табылады, ω₀-ге қарағанда симметриялы және амплитудасы A_n=U₀J_n(M) болатын ω₀±nΩ түріндегі шексіз бүйірлік жиіліктер санынан тұрады. М=4 үшін ол 1 суретінде тұрғызылған. Спектр жетіспеушілігі 2 қарама-қарсы фактордың әсерін ескеру қажет өте тар жиіліктер жолағында бөгеуілдер әсері азаяды, бірақ бір мезгілде түсуші құраушылардың жоқтығынан сигнал бұрмалануы артады. Практикада келісілген шешімді таңдайды.

Гармоникалық бұрыштық модуляцияның сигнал спектрінің енінің 2∆f_д жиілік интервалынан айырмашылығы, сигналдың лездік жиілігінің өзгерісі болатын аралықта:

а) спектрдің теориялық ені ∆f_{чм, фм}=∞;

б) М<<1 кезіндегі практикалық мәні ∆f_{чм, фм}=2F>>2∆f_д, ал M>>1 болғанда

∆f_{чм, фм} бірнеше есе артады 2∆f_д және оған тек шамамен жуықтағанда тең деп есептелінеді (7).

Спектр енін анықтау үшін (7) жақын өрнегін қолдана отырып, модуляциялаушы сигналдың x(t)=XcosΩt параметрлерінің ФМ және ЖМ тербелістерінің спектрлеріне әсерін қарастырайық. Х модуляциялаушы сигналдың амплитудасының өзгеруі нәтижесінде ФМ және ЖМ тербелістердің спектрі бірдей өзгереді.

Х-тің артуы нәтижесінде модуляция индексі пропорционалды артады, спектрлер спектральды компоненттердің санының көбеюі әсерінен кеңейеді. Модуляциялаушы тербелістің F жиілігінің өзгеруі ФМ және ЖМ тербелістерінің спектрлерінің өзгеруіне әртүрлі әсер етеді. ФМ өзгеруі кезінде модуляция индексінің шамасына әсер етпейді, соған сәйкес спектральды құраушылар санында болады (2.а,б, суретті қара).

2 Сурет

ЖМ кезінде төмендеуінен модуляция индексі жоғарылайды, ал ол спектральды құраушылардың санының көбейуіне алып келеді (2 в,г суретті қара). Қорытындылай келе ЖМ тербелісінің спектр ені жиілікке тәуелді емес, ал ФМ кезінде F –ке пропорциональды түрде өзгереді.