Вычисление площадей плоских фигур.
При вычислении площадей плоских фигур с применением определенного интеграла мы рассмотрим следующие случаи.
1. Фигура ограничена графиком непрерывной и неотрицательной на отрезке 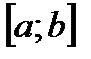
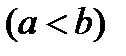 функции
функции  , осью
, осью  и прямыми
и прямыми  и
и 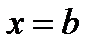 .
.
В этом случае согласно геометрическому смыслу определенного интеграла площадь S численно равна 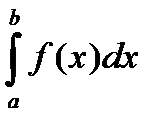 , т.е.
, т.е.  (1)
(1)
Пример 1. Вычислить площадь фигуры, ограниченной линиями  ,
,  ,
,  ,
,  (рис. 1). Применив формулу (1), найдем
(рис. 1). Применив формулу (1), найдем
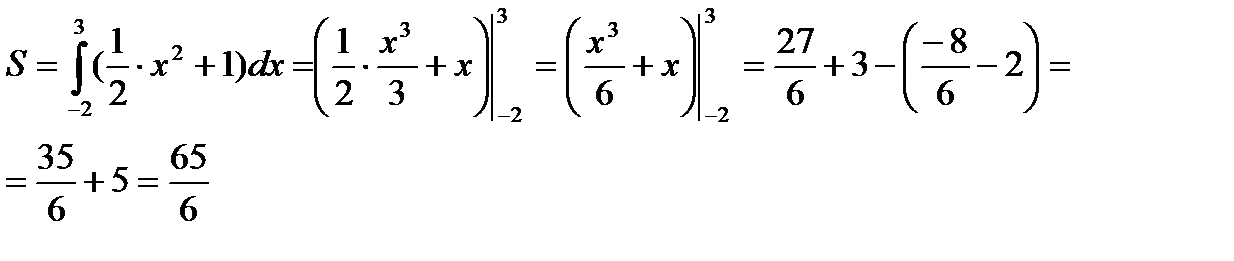

Рис. 1
2. Фигура ограничена графиком непрерывной и неположительной на отрезке 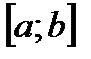 функции
функции 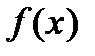 , осью
, осью 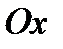 и прямыми
и прямыми 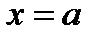 ,
,  (рис. 2).
(рис. 2).
Рассмотрим функцию  . Фигура
. Фигура 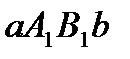 симметрична фигуре
симметрична фигуре  относительно оси
относительно оси 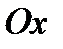 (см. рис. 2), а следовательно, их площади
(см. рис. 2), а следовательно, их площади 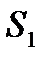 и
и  равны. Но
равны. Но
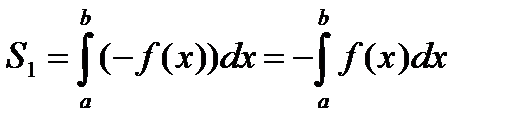 , поэтому
, поэтому 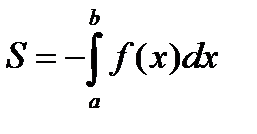 (2)
(2)
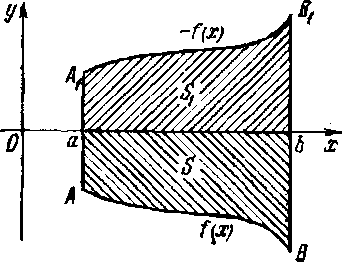
Рис. 2
Пример 2. Вычислить площадь фигуры, ограниченной линиями  ,
,  ,
, 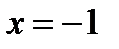 ,
, 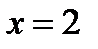 (рис. 3).
(рис. 3).
По формуле (2) находим
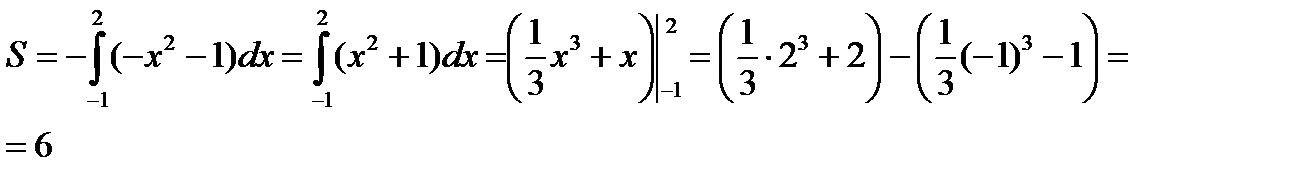

Рис. 3
3. Фигура ограничена осью 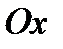 , прямыми
, прямыми 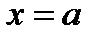 ,
,  и графиком функции
и графиком функции 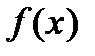 , которая непрерывна на отрезке
, которая непрерывна на отрезке 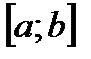 и меняет свой знак конечное число раз на этом отрезке (рис. 4). В этом случае разбивают отрезок
и меняет свой знак конечное число раз на этом отрезке (рис. 4). В этом случае разбивают отрезок 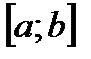 на такие частичные отрезки, на которых функция
на такие частичные отрезки, на которых функция 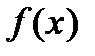 знакопостоянна (на рис. 4 имеется три таких отрезка:
знакопостоянна (на рис. 4 имеется три таких отрезка: 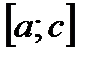 ,
, 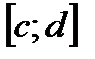 и
и 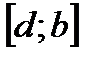 ). Очевидно, что искомая площадь S численно равна алгебраической сумме интегралов, взятых по каждому из полученных отрезков, причем знаки, с которыми эти интегралы входят в алгебраическую сумму, совпадают со знаками функции
). Очевидно, что искомая площадь S численно равна алгебраической сумме интегралов, взятых по каждому из полученных отрезков, причем знаки, с которыми эти интегралы входят в алгебраическую сумму, совпадают со знаками функции 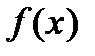 на соответствующих отрезках.
на соответствующих отрезках.
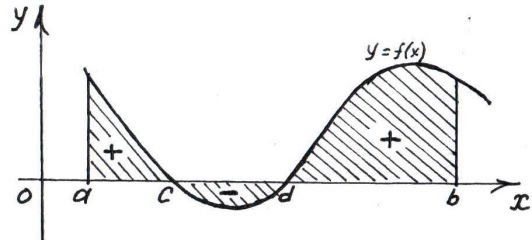
Рис. 4
Так, например, площадь фигуры, изображенной на рис. 13, вычисляется по формуле

Пример 3. Вычислить площадь фигуры, ограниченной линиями  ,
, 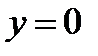 ,
, 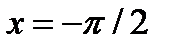 ,
,  (рис. 5).
(рис. 5).
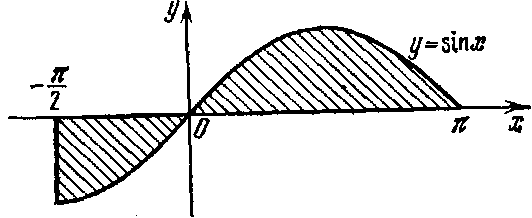
Рис. 5
Очевидно, что  для всех
для всех 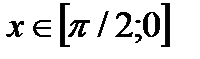 и
и  для всех
для всех 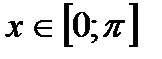 . Поэтому
. Поэтому
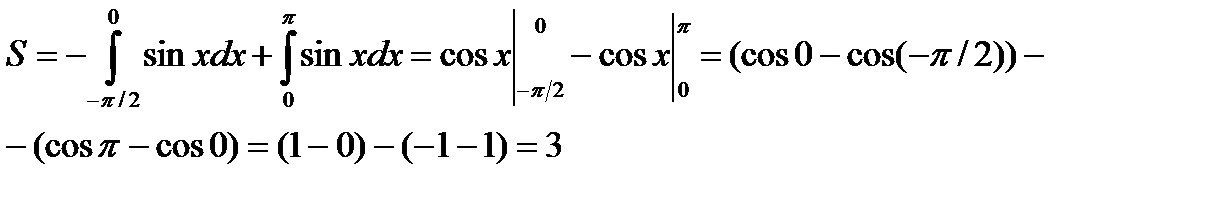
4. Фигура ограничена графиками двух непрерывных на отрезке 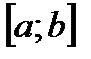 функций
функций 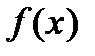 и
и 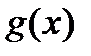 и прямыми
и прямыми  ,
, 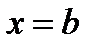 , где
, где 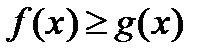 и
и 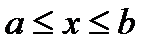 (рис. 6).
(рис. 6).


Рис. 6 Рис. 7
В этом случае искомая площадь S вычисляется по формуле
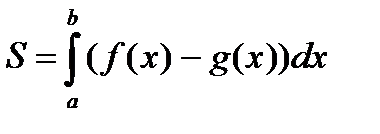 (3)
(3)
Пример 4. Вычислить площадь фигуры, ограниченной линиями 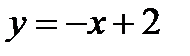 и
и  (рис. 6).
(рис. 6).
Пределы интегрирования 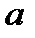 и
и  находим из системы уравнений
находим из системы уравнений 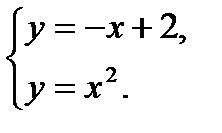
Отсюда 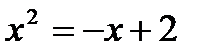 , т.е.
, т.е. 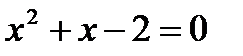 , откуда
, откуда 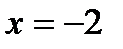 и
и  . Следовательно,
. Следовательно,  и
и 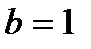 . Так как на отрезке
. Так как на отрезке  для
для 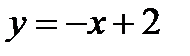 ,
,  имеем
имеем 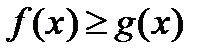 , то по формуле (3) находим
, то по формуле (3) находим
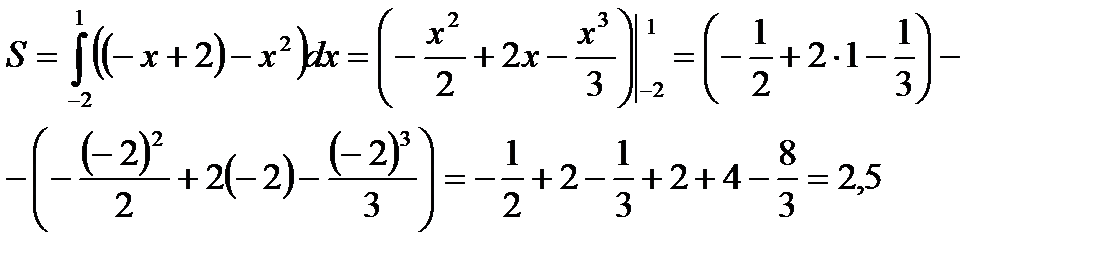
РАЗДЕЛ 6. Теория вероятностей
Элементы комбинаторики.
При решении ряда теоретических и практических задач требуется из конечного множества элементов по заданным правилам составлять различные комбинации и производить подсчет числа всех возможных таких комбинаций. Такие задачи принято называть комбинаторными, а раздел математики, занимающийся их решением, называется комбинаторикой.
Размещения.
Пусть дано множество, состоящее из  элементов. Размещением из
элементов. Размещением из 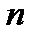 элементов по
элементов по 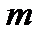 (
(  ) элементов называется упорядоченное подмножество, содержащее
) элементов называется упорядоченное подмножество, содержащее 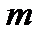 различных элементов данного множества. Из определения вытекает, что размещения из
различных элементов данного множества. Из определения вытекает, что размещения из  элементов по
элементов по 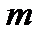 - это все
- это все 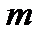 - элементные подмножества, отличающиеся составом элементов или порядком их следования.
- элементные подмножества, отличающиеся составом элементов или порядком их следования.
Число размещений из  элементов по
элементов по 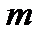 обозначается символом
обозначается символом  и вычисляется по формуле
и вычисляется по формуле  .
.
Пример.Сколько двузначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, если каждая цифра в обозначении числа встречается не более одного раза?
Решение.Задача сводится к нахождению числа размещений (без повторений) из шести элементов по два. Таким образом, искомое число равно 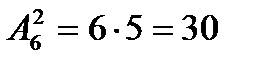 .
.
Перестановки.
Перестановкой из 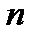 элементов называется размещение из
элементов называется размещение из 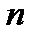 элементов по
элементов по 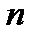 элементов. Число перестановок из
элементов. Число перестановок из 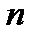 элементов обозначается символом
элементов обозначается символом 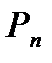 .
.
Так как каждая перестановка содержит все 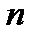 элементов множества, то различные перестановки отличаются друг от друга только порядком следования элементов. Из определения перестановок следует
элементов множества, то различные перестановки отличаются друг от друга только порядком следования элементов. Из определения перестановок следует 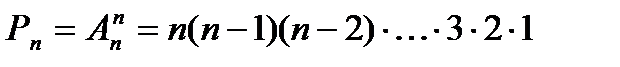 или
или 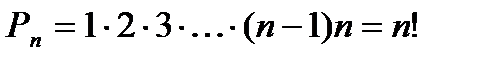
Пример. Сколькими способами можно расставлять на одной полке шесть различных книг?
Решение.Искомое число способов равно числу перестановок из 6 элементов, то есть  .
.
Сочетания.
Пусть дано множество, состоящее из  элементов. Сочетанием из
элементов. Сочетанием из 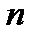 элементов по
элементов по 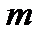 (
(  ) элементов называется любое подмножество, содержащее
) элементов называется любое подмножество, содержащее 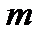 различных элементов данного множества.
различных элементов данного множества.
Число сочетаний из 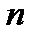 элементов по
элементов по 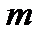 обозначается
обозначается  и вычисляется по формуле
и вычисляется по формуле 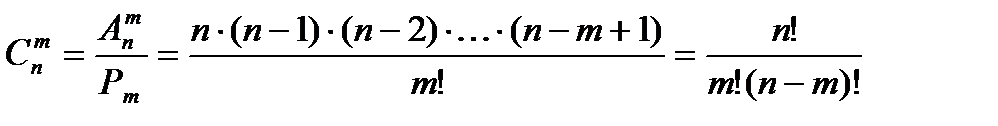 .
.
Пример. Сколько различных правильных дробей можно составить из чисел 1, 2, 3, 4, 5, 6, берущихся попарно?
Решение.Различных пар из данных чисел, в которых первый элемент меньше второго будет равно числу сочетаний из семи элементов по два, то есть  .
.
