Алгоритм дослідження функції на парність та непарність

1. Знайти область визначення функції та перевірити чи є вона симетричною відносно нуля.

2. Якщо область визначення симетрична відносно нуля, то знайти :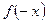

1) якщо 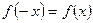, то функція є парною;

2) якщо 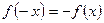, то функція є непарною.

Приклади:

1. Довести, що функція 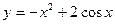є парною.

Розв’язування.1) 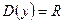- симетрична відносно нуля;

2) ,

,

.

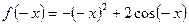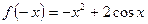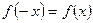Висновок: функція є парною.

2. Довести, що функція 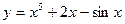є непарною.

Розв’язування.1) 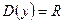- симетрична відносно нуля;

2) ,

,

,

.

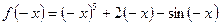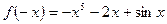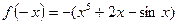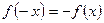Висновок: функція є непарною.

3. Дослідіть функції 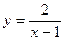та на парність або непарність.

Розв’язування.1) 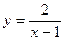, 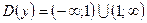не симетрична відносно нуля, отже функція є ні парною, ні непарною.

2) , , , , ,

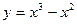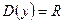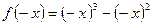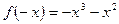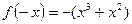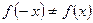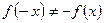, , отже функція є ні парною, ні непарною.

Відповідь. Ні парні, ні непарні.

Додаток№3

№1 Визначити, які із функцій , , 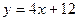, , 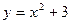, 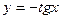є парними, які непарними.

Розв’язування.

1) , , 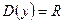, 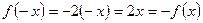непарна;

2) , , ,

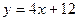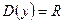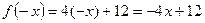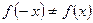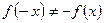, , ні парна, ні непарна;

3) 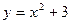, , 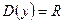, 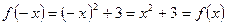парна;

4) , , 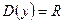, 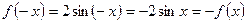непарна;

5) , , 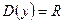, 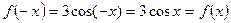парна;

6) 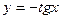, , 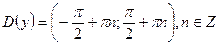, 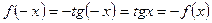непарна.

№2 Довести, що: а) функція є парною;

б) функція 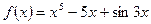є непарною.

Доведення.

а) , ;

,

,

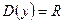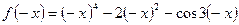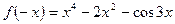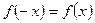, отже дана функція є парною;

б) , ;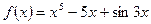

,

,

,

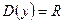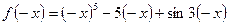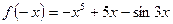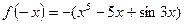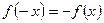, отже дана функція є непарною.

ДОВІДКОВИЙ МАТЕРІАЛ

Означення числової функції

Числовою функцією з областю визначення D називається відповідність, за якою кожному числу x з множини D ставиться у відповідність єдине число у, яка позначається y=f(x).

х-аргумент (незалежна змінна), у-функція (залежна змінна).

Властивості числових функцій