Математика және физика кафедрасы
Пәннің оқу бағдарламасы - SYLLABUS
Геометрия негіздеріпәні бойынша
5В010900- Математика мамандығына арналған
| Несие саны | |
| Курс | |
| Семестр | |
| Емтихан (семестр) | |
| Дәріс (сағат) | |
| Тәжірибелік сабақ (сағат) | |
| Студиялық сабақ (сағат) | - |
| Зертханалық сабақ (сағат) | - |
| СӨЖ (сағат) | |
| ОСӨЖ (сағат) |
Арқалық, 2016
1. Оқытушы(-лар) туралы мәлімет: Джакетова Сауле Жақсылыққызы Арқалық мемлекеттік педагогикалық институтының математика және физика кафедрасында 2005 жылдан жұмыс істейді. Арқалық мемлекеттік педагогикалық институтының аға оқытушысы, магистр
2. Байланыс ақпараты: 7-76-82, 87016192944
3. Пәннің пререквизиттері: Элементар математика, математикаға енгізу кіріспесі, аналитикалык геометрия, математикалык талдау1.
4. Пәннің постреквизиттері: математиканы окыту әдiстемесi, математика тарихы жене методологиясы.
5. Пәнді оқытудың мақсаты: Геометриядағы негізгі әдістер және тұжырымдармен болашақ мектеп оқытушыларын таныстыру.
6. Пәнді оқытудың міндеттері:
- Кеңістіктік, логикалық және алгоритмдік ойлауды дамыту.
- Негізгі методикалық көзқарастарды қалыптастыру.
- Геометрия негіздемелерінің негізгі зерттеу әдістерін меңгеру.
- Өзінше математикалық білімді кеңейту және аксиомалар жүйесімен математикалық структураларды талдай білу.
- Бізді қоршаған орта туралы көзқарасты қалыптастыру.
- Оқушыларды, өз еркімен еңбектеніп оқуға тәрбиелеу
7. Пән бойынша студенттердің дайындық деңгейіне қойылатын талаптар (оқу нәтижелері, құзыреттілікке қойылатын талаптар)
Нақты пәнді оқыту нәтижесінде келесі құзыреттіліктер қалыптастырылуы қажет:
құзыреттіліктердің сипаты
Студент пәнді меңгеру нәтижесінде:
Білуге:
- Геометрияның даму тарихы
- Евклид геометриясының ерекшеліктерін
- Лобачевский геометриясының Евклид геометриясынан айырмашылығын.
Қабілетті болуға:
- Жұмыс жасау барысында ғылыми, оқу-әдістемелік және анықтамалық әдебиеттерді қолдануда;
- Өз бетінше геометриядан есептер шығара білуі;
- Көпмәдениетті ортада көпшілікпен тіл табыса білу;
- Теоремалар дәлелеу кезінде аксиомаларды жүйелі түрде қолдана білуі.
Білікті болуға:
- Геометрияның негізі аксиомалар мен теоремаларды оқып, дәлелдей білуі;
- Евклид, Вейль, Гильберт аксиомалар жүйесінің маңызын білуге міндетті.
8. Пәннің қысқаша мазмұны:
“Геометрия негiздерi” курсы болашақ математика мұғалімдердің, жалпы математиктiң маман ретiнде калыптасуы үшiн өте кажет. Бұл курсты оқу нәтижесiнде баска пәндердi математикалык талдау, математикалык логика, математиканы окыту әдiстемесi және т.б. пәндердi сапалы түрде меңгеруге болады.
Аталған курсты мектеп геометриясын оқытатын мұғалiм өте жаксы бiлуге тнiстi. Курсты оқу нәтижесiнде болашақ окытушының геометрия пәнiне көзқарасы калыптасады. Мұғалiм әртүрлi сала бiлiм беретiн оку орындарында сабак жүргiзе алады
9. Пәннің тақырыптық-күнтізбелік жоспары:
| № | Тақырыптың атауы | Дәріс | Тәжірибелік сабақ | Студиялық сабақ | Зертханалық сабақ | СӨЖ | ОСӨЖ |
| І модуль Аксиоматиканың жалпы сұрақтары | |||||||
| 1.1 | Математикалық құрылым ұғымы. Изоморфизм. Аксиомалар жүйесінің интерпретациясы жайлы түсінік | ||||||
| 1.2 | Аксиомалар жүйесінің қарама-қайшылықсыздығы, тәуелсіздігі және толықтығы. | ||||||
| 2-модульЕвклидтік геометриясының негіздемесі | |||||||
| 2.1 | Үш өлшемді евклид кеңістігі үшін Вейль аксиомаларының қарама-қайшылықсыздығы және толықтығы. | ||||||
| 2.2 | Түзудің, жазықтықтың, сәулені, кесіндінің, бұрыштың анықтамалары. | ||||||
| 2.3 | Кейбір теоремаларды дәлелдеу Мектеп геометрия курсының аксиомалар жүйесі және оның Вейль аксиомаларымен байланысы | ||||||
| ІІІ модуль Геометрияның негізделу тарихы | |||||||
| 3.1. | Евклидке дейінгі геометрия. Евклид «Бастамалары». Евклид жүйесін сынау. V- постулат | ||||||
| 3.2. | Гильберттің аксиомалар жүйесі | ||||||
| 3.3. | Н.И. Лобачевский және оның геомтериясы. Лобачевский аксиомасы. | ||||||
| 3.4. | Лобачевский жазықтығының геометрияның жай теоремалары. Лобачевский жазықтығының аксиомалар жүйесінің қайшылықсыздығы | ||||||
| 3.5. | Топологиялық кеңістіктің анықтамасы. Жекеленушілік, байланыстылық, компактылық. Облыс. Үздіксіздік және гомеоморфизм. | ||||||
| 3.6. | Топологиялық көпбейне. Мейбус жапырағы мен проективті жазықтықтың топологиялық қасиеттері. | ||||||
| 3.7. | Беттің Эйлерлік сипаттамасы. Беттерді топологиялық жіктеу ұғымы. Көпжақтар үшін Эйлер теоремасы. | ||||||
| ІV модуль Евклидтік кеңістіктегі сызықтар мен беттер | |||||||
| 4.1. | Сызық ұғымы. Жатық қисықтар. Жанама. Қисықтың ұзындығы. Иілімі және бұралымы. | ||||||
| 4.2. | Беттің бірінші квадраттық формасы. Геодезиялық сызық ұғымы. Беттің толық иілімі. Иілімі тұрақты беттер. | ||||||
| 4.3. | Геодезиялық үшбұрыштың дефектісі. Иілімі теріс тұрақты беттер. Лобачевскийдің кіші геометриясын өрнектеу. | ||||||
| Барлығы |
10.СӨЖ тапсырмаларын орындау және тапсыру кестесі:
| № | ОСӨЖ тапсырмалары | Бақылау түрі | Тапсыру мерзімі (апта) |
| Геометрия тарихынан | Презентация дайындау | 1 апта | |
| Кесінді мен бұрышқа арналған өлшеу аксиомасы | Ұғымдарды түсініп баяндау | 2 апта | |
| Евклид геометриясындағы аксиомалар жүйесін декарттық жүзеге асыру | Конспект | 3 апта | |
| Берілген түзудің кесіндісінің бар болуы туралы аксиома тәуелсіздігі | Конспект | 4 апта | |
| Кейбір теоремаларды дәлелдеу | Ұғымдарды түсініп баяндау | 5 апта | |
| Евклид “Бастамалары”. V- постулат дәлелдеу түрлері | Презентация дайындау | 6 апта | |
| Гильберттің аксиомалар жүйесі | Реферат | 7 апта | |
| Лобачевский жазықтығындағы салуларға арналған есептер | Типтік есептер | 8 апта | |
| Жиындардың қосылуы | Реферат сөзжұмбақ | 9 апта | |
| Топологиялық кеңістіктің анықтамасы | Есептер | 10 апта | |
| Кеңістіктің орташа және толық қисықтығы | Есептер | 11 апта | |
| Мейбус жапырағы | Презентация дайындау | 12 апта | |
| Қисықтың иiлiмі және бұралымы | Реферат | 13 апта | |
| Геодезиялық сызық ұғымы. | Типтік есептер | 14 апта | |
| Геодезиялық үшбұрыштың дефектісі | Реферат сөзжұмбақ | 15 апта |
11.ОСӨЖ өткізу жоспары:
| № | ОСӨЖ тапсырмалары | Бақылау түрі |
| 1. | Геометрия тарихынан Геометрияның дамуы. Геометрияның негіздемесіндегі жұмыстар. Реттеу аксиомасы | Презентация дайындау |
| 2. | Кесінді мен бұрышқа арналған өлшеу аксиомасы Берілген түзудің кесіндісінің болатындығы туралы аксиома. Паралелльдік аксиомасы | Конспект |
| 3. | Евклид геометриясындағы аксиомалар жүйесін декарттық жүзеге асыру.Евклид геометриясындағы аксиомалар жүйесінің толықтығы | Ұғымдарды баяндау |
| 4. | Берілген түзудің кесіндісінің бар болуы туралы аксиома тәуелсіздігі.Параллельдік аксиоманың тәуелсіздігі | Конспект |
| 5. | Евклид “Бастамалары”. V- постулат дәлелдеу түрлері Евклиддік емес геометрияның ашылуы.Гильберт аксиомасының зерттелуі. Лобачевский жазықтығындағы дәлелдеуге арналған есептер | Есептер шығару |
| 6. | Лобачевский жазықтығындағы салуларға арналған есептер Клейна интерпретациясыПуанкаренің жалпы интерпретациясы | Типтік есептер шығару |
| 7. | Бар болу және жалғыздық теоремасы. Көлемдер теориясы.Жиындардық атұйықтығы жіне ашықтығы | Реферат |
| 8. | Жиындардың қосылуы. Жиындардық тұйықтығы жіне ашықтығы | Конспект |
| 9. | Қарапайым кеңістікКеңістіктегі қисықтар | Перезентация дайындау |
| 10. | Кеңістіктің орташа және толық қисықтығы Кеңістіктегі тамаша қисықтар | Конспект |
| 11. | Мейбус жапырағы мен проективті жазықтықтың топологиялық қасиеттері | Презентация дайындау |
| 12. | Көпжақтар үшін Эйлер теоремасы. | Реферат |
| 13. | Сызық ұғымы. Жатық қисықтар | Конспект |
| 14. | Беттің толық иілімі. Иілімі тұрақты беттер. | Реферат |
| 15. | Лобачевскийдің кіші геометриясын өрнектеу. | Есептер шығару |
12. Негізгі және қосымша әдебиеттер тізімі
12.1 Негізгі әдебиеттер тізімі:
1. Александров А. Д., Нецветаев Н. Ю. Геометрия: Учеб. пособие.— М.; Наука. Гл. ред. физ.-мат. лит., 1990.— 672 с:
2. Атанасян Л.С, Базылев В.Т. Геометрия. В 2-х ч. Ч. I. Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов.— М.: Просвещение, 1986.— 336 с
3. Атанасян Л.С, Базылев В.Т. Геометрия. Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов. В 2 ч. Ч. 2.— М.: Просвещение, 1987.—352 с:
4. Базылев В.Т., Дуничев К.И., В. П. Иваницкая и др. Сборник задач по геометрии : Учеб. пособие для студентов мат. и физ.-мат. фак. пед. ин-тов / Под ред. В. Т. Базылева. —М.:Просвещение, 1980. 241 с, ил.
5. Атанасян С. Л., Цаленко М. М. Задачник-практикум по геометрии : Учеб. пособие для студентов-заочников II—V курсов физ.-мат. фак. пед. ин-тов/ Моск. гос. открытый пед. ин-т.— М.: Просвещение, 1994.— 192 с:
6. Сборник задач по геометрии / Под ред. В.Т. Базылева. М., Просвещение, 1980.
12.2 Қосымша әдебиеттер тізімі:
1. Ефимов Н.В. Высшая геометрия. — 7-е изд. — М.: ФИЗМАТЛИТ, 2004. - 584 с.
2. Егоров И.П. Основания геометрии. М., Просвещение 1984г7
3. Кузютин В.Ф., Зенкевич Н.А., Еремеев В.В. Геометрия: учебник для вузов. - Лань, 2003. - 415 c.
4. Прасолов В. В., Тихомиров В.М. Геометрия.—М.: МЦНМО, 2007.—2-е изд., перераб. и доп.—328 с:
13. Студенттердің білімін, икемін, дағдысын бағалау жүйесі
Ағымдағы бақылау (семестрдің 1-7 және 8-15 апталарында өткізіледі):
1. Студенттің әр дәріс сабағына қатысуы 100 балмен, қатыспауы 0 балмен бағаланады. Орташа арифметикалық өлшемі студенттің дәріс сабақтарына қатысу көрсеткіші болып табылады.
2. Практикалық (зертханалық, студиялық) сабақтағы белсенділігі мен тапсырмаларды орындау деңгейіне байланысты әр практикалық (зертханалық, студиялық) сабақ максималды 100 балмен бағаланады. Орташа арифметикалық өлшемі студенттің практикалық (зертханалық, студиялық) тапсырмаларды орындау көрсеткіші болып табылады.
3. Үй тапсырмасын орындау деңгейіне байланысты максималды 100 балл беріледі. Орташа арифметикалық өлшемі студенттің үй тапсырмаларын орындау көрсеткіші болып табылады. Үй тапсырмасының көлемін оқытушы анықтайды.
4. СӨЖ (оның ішінде ОСӨЖ) тапсырмаларын орындау максималды 100 балмен бағаланады. Орташа арифметикалық өлшемі студенттің СӨЖ (оның ішінде ОСӨЖ) тапсырмаларын орындау көрсеткіші болып табылады.
Ағымдық бақылау (АБ) бағасы келесі формуламен есептелінеді:
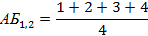
Межелік бақылау(семестрдің 7 және 15 апталарында өткізіледі):
Межелік бақылауда (МБ) студенттің білімі жазбаша жұмыс / ауызша жауап / компьютерлік тестілеу / норматив тапсыру / шығармашылық тапсырма орындау арқылы тексеріліп, максималды 100 балл қойылады.
Студенттің межедегі рейтингі (Р) келесі формуламен есептелінеді:
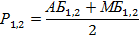
Студентті қорытынды бақылауға (емтиханға) жіберу рейтингі (Рорташа) келесі формуламен анықталады:
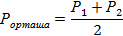
Қорытынды бақылау (емтихан) (Е) емтихан сессиясы кезінде өткізіледі. Емтихан жазбаша түрде / компьютерлік тестілеу / норматив тапсыру / шығармашылық тапсырма орындау арқылы қабылданады, максималды 100 балл қойылады.
Қорытынды баға (ҚБ) келесі формула бойынша есептелінеді:
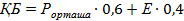
Білім алушылардың оқудағы жетістіктерін төрт балдық жүйе бойынша сандық эквивалентке сәйкес бағалаудың әріптік жүйесі
| Әріп жүйесі бойынша | Балдың сандық эквивалент | Проценттік мазмұны | Дәстүрлі жүйе бойынша бағалау |
| А | 4,0 | 95-100 | өте жақсы |
| А- | 3,67 | 90-94 | |
| В+ | 3,33 | 85-89 | жақсы |
| В | 3,00 | 80-84 | |
| В- | 2,67 | 75-79 | |
| С+ | 2,33 | 70-74 | қанағаттанарлық |
| С | 2,00 | 65-69 | |
| С- | 1,67 | 60-64 | |
| D+ | 1,33 | 55-59 | |
| D | 1,00 | 50-54 | |
| F | 0-49 | қанағаттанғысыз |
14. Межелік және қорытынды бақылау сұрақтары
І аралық бақылау сұрақтары
1. «Геометрия негіздемелері» курсының бізді қоршаған орта туралы көзқарасымызды қалыптастырудағы алатын орны.
2. Аксиомалаудың жалпы сұрақтары.
3. Математикалық структура ұғымы, изоморфизм.
4. Аксиомалар жүйесінің интерпретациясы туралы түсінік
5. Аксиомалар жүйесiнің қайшылықсыздығы тәуелсiздiгi және
6. Евклид геометриясы
7. Евклид геометриясының негiздемесi
8. Үш өлшемді евклид кеңістігіне арналған Вейль аксиомалар жуйесi
9. Вейль аксиомалар жуйесiнiң қайшылыксыздығы және толықсызы.
10. Тузудiң анықтамалары
11. Жазықтықтың анықтамалары,
12. Сәуленiң анықтамалары,
13. Кесiндiнiң анықтамалары,
14. Бұрыштың анықтамалары,
15. Кейбiр теоремаларды дәлелдеу
16. Мектеп геометрия курсының аксиомалар жүйесi
17. Мектеп геометрия курсының Вейль аксиомаларымен байланысы
18. Геометрияны негiзделудiң тарихы.
ІІ аралық бақылау сұрақтары
1. Евклидке дейiнгi геометрия.
2. Евклид “Бастамалары”. Евклид жүйесiн сынау.
3. V- постулат.
4. Гилберттiң аксиомалар жуйесi (жалпы турде Лобачевский геометриясы
5. Н.И.Лобачевский және оның геометриясы.
6. Лобачевский аксиомасы.
7. Лобачевский жазыктығында геометрияның жай теоремалары.
8. Лобачевский жазыктығының аксиомалар жүйесiнiң кайшылыксыздығы
9. Геометрия элементтері
10. Ұзындық, аудан, көлем Сызык ұғымы.
11. Жазық қисыктар.
a. Жанама. Қисықтың ұзындыгы.
12. Иiлiм және бұралым. Топологиялык кеңiстiк
13. Топологиялык кеңiстiктiң аныктамасын, мысалдар. жекеленушiлiк, байланыстылық, комлактылык
14. Облыс.
15. Үздiксiздiк жене гомеоморфизм Топологиялық көпбейне.
16. Мейбус жапырағы мен проективтi жазықтықтың топологиялық қасиеттерi
17. Беттiң Эйлерлiк сипаттамасы.
18. Беттерді топологиялық жiктеу ұғымы.
19. Көпжактар үшiн Эйлер теоремасы Түзу түсінігі
20. Жазық қисмықтар
21. Жанамалар
22. Қисық ұзындығы
23. Иілім және бұрылым Бет түсінігі
24. Жазық беттер
25. Жазықтық жанамасы және Беттiң бiрiншi квадраттық формасы.
26. Геодезиялык сызықтың ұғымы.
27. Беттiң толык иiлiмi.
28. Иiлiмi тұракты беттер.
29. Геодезиялык үшбұрыштың дефектiсi
30. Иiлiмi терiс тұракты бетте лобачевскйдiң кiшi геометриясын өрнектеу.
Емтихан сұрақтары
1. «Геометрия негіздемелері» курсының бізді қоршаған орта туралы көзқарасымызды қалыптастырудағы алатын орны.
2. Аксиомалаудың жалпы сұрақтары.
3. Математикалық структура ұғымы, изоморфизм.
4. Аксиомалар жүйесінің интерпретациясы туралы түсінік
5. Аксиомалар жүйесiнің қайшылықсыздығы тәуелсiздiгi
6. Евклид геометриясы
7. Евклид геометриясының негiздемесi
8. Үш өлшемді евклид кеңістігіне арналған Вейль аксиомалар жуйесi
9. Вейль аксиомалар жуйесiнiң қайшылыксыздығы және толықсызы.
10. Тузудiң анықтамалары
11. Жазықтықтың анықтамалары,
12. Сәуленiң анықтамалары,
13. Кесiндiнiң анықтамалары,
14. Бұрыштың анықтамалары,
15. Кейбiр теоремаларды дәлелдеу
16. Мектеп геометрия курсының аксиомалар жүйесi
17. Мектеп геометрия курсының Вейль аксиомаларымен байланысы
18. Геометрияны негiзделудiң тарихы.
19. Евклидке дейiнгi геометрия.
20. Евклид “Бастамалары”.
21. Евклид жүйесiн сынау.
22. V- постулат.
23. Гилберттiң аксиомалар жуйесi
24. Лобачевский геометриясы
25. Н.И.Лобачевский және оның геометриясы.
26. Лобачевский аксиомасы.
27. Лобачевский жазыктығында геометрияның жай теоремалары.
28. Лобачевский жазыктығының аксиомалар жүйесiнiң кайшылыксыздығы
29. Геометрия элементтері
30. Ұзындық, аудан, көлем Сызык ұғымы.
31. Жазық қисыктар.
32. Жанама. Қисықтың ұзындыгы.
33. Иiлiм және бұралым.
34. Топологиялык кеңiстiк
35. Топологиялык кеңiстiктiң аныктамасын, мысалдар. жекеленушiлiк, байланыстылық, комлактылык
36. Облыс.
37. Үздiксiздiк жене гомеоморфизм
38. Топологиялық көпбейне.
39. Мейбус жапырағы мен проективтi жазықтықтың топологиялық қасиеттерi
40. Беттiң Эйлерлiк сипаттамасы.
41. Беттерді топологиялық жiктеу ұғымы.
42. Көпжактар үшiн Эйлер теоремасы
43. Түзу түсінігі
44. Жазық қисықтар
45. Жанамалар
46. Қисық ұзындығы
47. Иілім және бұрылым Бет түсінігі
48. Жазық беттер
49. Жазықтық жанамасы
50. Беттiң бiрiншi квадраттық формасы.
51. Геодезиялык сызықтың ұғымы.
52. Беттiң толык иiлiмi.
53. Иiлiмi тұракты беттер.
54. Геодезиялык үшбұрыштың дефектiсi
55. Иiлiмi терiс тұракты бетте Лобачевскйдiң кiшi геометриясын өрнектеу.
