Расчет усилительного каскада по переменному току.

Анализ и расчет усилителей обычно ведутся с использованием эквивалентных схем по переменному току. При этом транзистор заменяется физической эквивалентной Т-образной схемой для транзистора, включенного по схеме с общим эмиттером, источник питания Е_к по переменному току коротко замкнут. Исходя из вышесказанного, общая эквивалентная схема представлена на рис.1.3.

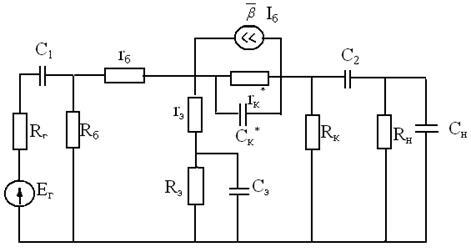
Рис.1.3

Для упрощения расчета весь диапазон рабочих частот можно разбить на три области (нижних, средних верхних частот)и рассматривать раздельно поведение АЧХ в этих областях.

1). Средние частоты.

Начнем расчет усилительного каскада с области средних частот, в которой можно считать схему, состоящей только из активных элементов и не учитывать временных и частотных искажений. Внешние емкости С₁, С₂ и С_э будем предполагать бесконечно большими, емкости С_к и С_н равными нулю, сопротивление нагрузки R_н и источника сигнала R_г чисто активными, а коэффициент передачи β действительной величиной. Тогда эквивалентная схема каскада будет такой, как показана на рис.1.4 .

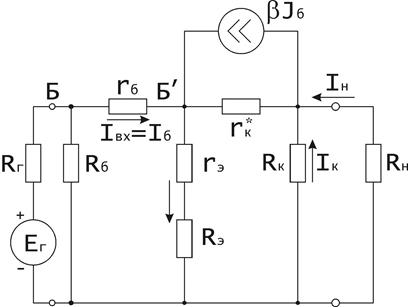
Рис.1.4

С целью упрощения расчетов в области средних частот основные параметры усилительного каскада обычно рассчитывают с помощью h-коэффициентов транзистора. В упрощенной схеме замещения (рис.1.5) транзистор формально представляется как активный четырехполюсник, на входе которого действуют напряжение U_вх и ток I_вх,, а на выходе - напряжение U_вых и ток I_вых и для транзистора известны h-коэффициенты в рабочей точке. Сопротивление R_б= R₁║R₂ ‌‌показывает наличие базового делителя, резисторы R₁, R₂ которого по переменному току соединены параллельно. Резисторы R_к, R_н также соединены параллельно и их можно заменить сопротивлением R′_н= R_к║R_н.

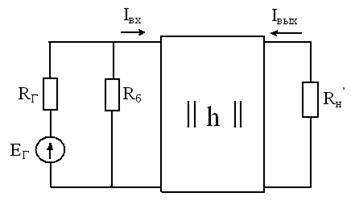
Рис. 1.5

Исходя из общих уравнений четырехполюсника и применяя их для малых сигналов (почти линейных участков), запишем для анализируемой схемы (рис.1.5) следующую систему уравнений, которая позволит определить основные параметры усилительного каскада в области средних частот:

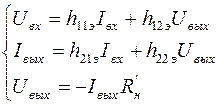(1.18)

Коэффициент усиления по току определяется как:

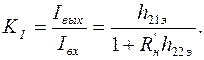(1.19)

Входное сопротивление без учета сопротивления R_б:

(1.20)

Коэффициент усиления по напряжению:

(1.21)

Выходное сопротивление:

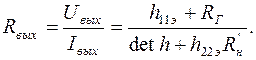(1.22)

Предыдущие расчеты были сделаны без учета влияния базового делителя на входное сопротивление усилительного каскада, а также влияния R_Г, R_к, R_вх на коэффициент усиления по току и R_к на выходное сопротивление. С учетом вышесказанного, окончательно получаем :

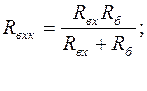(1.23)

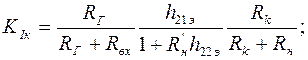(1.24)

(1.25)

Индекс к означает, что расчет ведется для полного каскада.

Выразим вышеприведенные формулы через собственные параметры транзистора. Для этого воспользуемся выражениями, связывающими h-коэффициенты с собственными параметрами транзистора:

(1.26)

Тогда

при условии 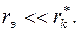(1.27)

. (1.28)

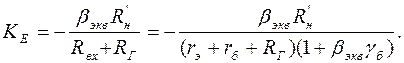(1.29)

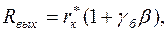где (1.30)

2). Нижние частоты.

Продолжим расчет усилительного каскада в области нижних частот. Эквивалентная схема каскада показана на рис.1.6. Здесь существенное влияние оказывают емкости С_1, С₂ и С_э. С понижением частоты реактивное сопротивление указанных емкостей увеличивается. При этом емкости С₁ и С₂ препятствуют прохождению сигнала со входа каскада на его выход, уменьшая тем самым коэффициент усиления каскада в области нижних частот. Действие блокирующей емкости несколько иное – в области нижних частот она перестает шунтировать резистор R_э и коэффициент усилкния каскада уменьшается за счет действия отрицательной обратной связи. Для того чтобы количественно оценить уменьшение усиления , вводят понятие коэффициента частотных искажений

который показывает, во сколько раз коэффициент усиления в области средних частот (К₀) больше коэффициента усиления в области нижних частот (К_н(ω) ). Так как в области нижних частот коэффициент усиления является комплексной величиной, то понимают его модуль.

Рассмотрим влияние каждой из этих емкостей поочередно, полагая остальные две емкости бесконечно большими (т.е. “закороченными”).

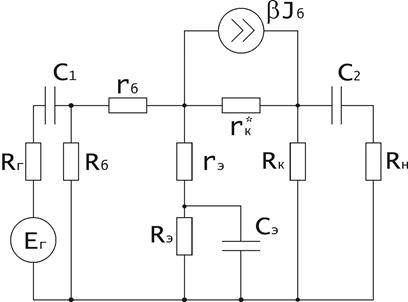
Рис. 1.6.

Положим сначала С₂ = ∞, С_э = ∞ и выясним роль С₁. В результате получим эквивалентную схему, показанную на рис1.6а. Комплексный коэффициент передачи этой цепи можно найти по следующей формуле:

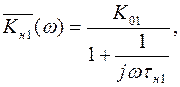(1.31)

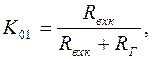
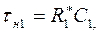
где 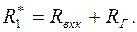(1.32)

Частотные искажения за счет влияния С₁ можно определить по формуле:

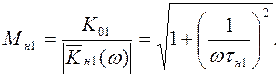(1.33)

Полагая С₁ = ∞, С_э = ∞ и рассматривая влияние С₂, получаем эквивалентную схему на рис.1.6б. Комплексный коэффициент передачи этой цепи можно найти по следующей формуле:

(1.35)

где 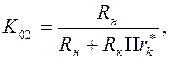(1.36)

Коэффициент частотных искажений за счет влиянии емкости С₂ определяется как:

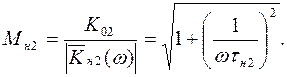(1.37)

Аналогично оценивается влияние блокирующей емкости в цепи эмиттера С_э, полагая С₁ = ∞, С₂ = ∞. При этом коэффициент частотных искажений, характеризующий влияние С_э на АЧХ усилительного каскада:

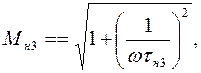где 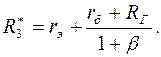(1.38)

Совместное влияние емкостей оценивается общим коэффициентом частотных искажений, который определяется как:

(1.39)

где 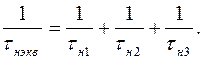(1.39а)

Нижняя частота полосы пропускания усилительного каскада связана с τ_экв следующим соотношением:

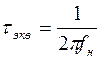. (1.40)

Для расчета емкостей конденсаторов, обеспечивающих нижнюю частоту полосы пропускания, применим метод весовых коэффициентов. Вводится весовой коэффициент

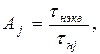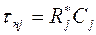где , (1.41)

Тогда (1.42)

Чтобы оптимально определить весовые коэффициенты, необходимо ввести целевую функцию. В нашем случае целевая функция вводится как:

(1.43)

Таким образом, задача сводится к отысканию локального экстремума методом Лагранжа (метод неопределенных коэффициентов). Исходя из вышесказанного, для определения весовых коэффициентов получаем следующую систему уравнений:

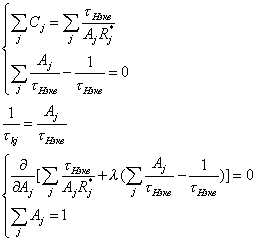(1.44)

В нашем случае j изменяется от 1 до 3 т.е.

(1.45)

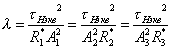
т.е.

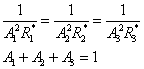
Решая эту систему относительно А, получим

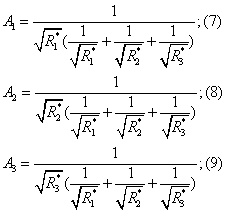(1.46)

Анализ полученных соотношений позволяет записать общую формулу для определения весовых коэффициентов при любом j:

. (1.47)

3). Верхние частоты.

Эквивалентная схема усилительного каскада в области верхних частот показана на рис.1.7.С повышением частоты уменьшается β, т.е становится комплексной величиной, увеличиваются шунтирующее действие емкости коллекторного перехода С_к^*и емкости нагрузки С_н,. Все это приводит к уменьшению усиления в области верхних частот, которое оценивают с помощью коэффициента частотных искажений

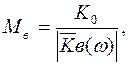(1.48)

где - модуль коэффициента усиления в области верхних частот.

Для количественного анализа и получения основных расчетных соотношений воспользуемся формулой (1.29), заменив в ней действительные величины комплексными, а именно

где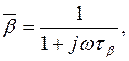

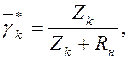
При этом будем считать нагрузку активной, постоянная времени τ_β связана с предельной частотой работы транзистора соотношением [] τ_β=(1+β)/2πf_α. Тогда комплексный коэффициент усиления в области верхних частот запишется как

(1.49)

где

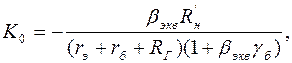(1.50)

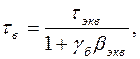
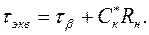(1.51)

С учетом емкостной нагрузки С_н постоянная времени τ_в запишется как

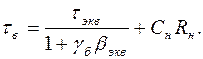(1.52)

Тогда коэффициент частотных искажений в области верхних частот для каскада

(1.53)

Верхняя частота полосы пропускания по уровню 0,707 оценивается как

. (1.54)