Методы оптимизации нелинейных функций без ограничений.

Если ограничения в задаче НЛП отсутствуют, то применяют все методы оптимизации нелинейных функций. Причём, если в задаче с ограничениями, они находятся внутри области, то решение можно найти этими методами. Говорят, что ограничения не являются активными и их можно отбросить. Рассмотрим наиболее широко применяемые методы.

1) Классический градиентный метод.

Все эти методы принадлежат к поисковым методам, т. е. оптимальное решение находится не сразу, а последовательным движением от точки к точке и заканчивается в оптимальной точке. Начинаем с начальной точки, её выбор – чтобы была ближе к оптимальной точке. Для её выбора и направления движения используют понятие градиента. Градиент – вектор, показывающий направление наибыстрейшего изменения функции. Градиент направлен по нормали к поверхности целевой функции, а в плоскости 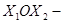по нормали к линиям уровня. Алгоритм: 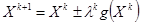. Каждая последующая точка определяется как предыдущая 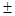длина градиента в предыдущеё точке шага (“+” – задача на максимум; “ – ” – задача на минимум). Если максимуму или минимум гладкий (большой коэффициент «тупизны»), градиент у нас уменьшается (в вершине градиент равен нулю) по модулю по мере приближения к максимуму и шаг уменьшается. Но при выборе 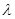надо иметь в виду следующее: если 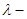мало, то идти будем долго, а если 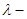большое, то можем перепрыгнуть.

В некоторых алгоритмах 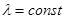, в более сложных 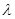зависит от 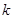. Правила остановки могут быть различными, например следующее:

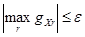
2) Покоординатный градиентный метод (метод координат спуска или подъёма).

Из некоторой начальной точки движемся вдоль некоторой координаты в сторону, где проекция градиента положительна. Движемся до тех пор, пока производная по этой координате не будет равна нулю. Затем движение идёт по второй координате аналогичным способом, и т. д. (если для двух координат, то опять по первой и по второй).

3) Метод наискорейшего спуска (подъёма).

В этом алгоритме из некоторой начальной точки движение осуществляется вдоль направления градиента до тех пор, пока производная по этому направлению не будет равна нулю. Далее из этой точки определяем градиент и т. д. Отличие здесь в том , что длина шага 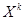определяется из условия, чтобы обеспечить:

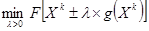
Второй и третий методы называются алгоритмами с длинным шагом. Кроме этого существуют методы, использующие вторую производную, например, метод Ньютона:

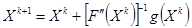
Метод поиска минимальной, не использующий понятие производной.

Метод Нелдера-Мида.

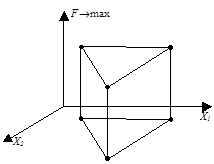Современные методы поиска минимальной (максимальной) нелинейной функции чрезвычайно разнообразны. Одним из наиболее эффективных является метод Нелдера-Мида. Идея метода состоит в том, что, вычисляется значение целевой функции в вершинах сначала правильного, а затем деформи­руемого многогранника. Многогранник – некоторое правильное тело в 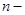мерном пространстве. Эта правильная фигура называется симплексом. В задачах для двух переменных, это правильный треугольник. Затем сравниваются значения целевых функций в вершине, а затем выполняются операции:

1) Отражение – поворот симплекса через одну из сторон;

2) Растяжение – если идём в правильном направлении;

3) Редукция – возврат назад, если перескочили максимум;

4) Сжатие – уменьшение сторон, чтобы движение было с более мелким шагом.

Алгоритм:

1) Обозначим 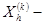самая худшая точка; 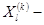самая лучшая точка.

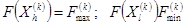
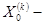центр тяжести всех вершин, исключая 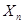. Координаты центра тяжести определяются:

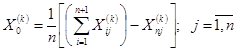
2) Затем отражаем, и получаем точку: 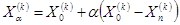. Здесь 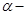коэффициент отражения; в обычном случае он равен единице.

· Если 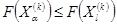, то вектор 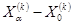растягивается в 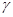раз и получаем:

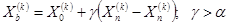
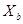
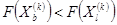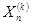Если для полученной точки , то заменяется на 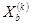, и переходим к пункту 2

· Если 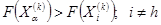, то вектор 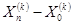сжимается в 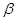раз и получаем точку:

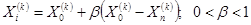
Затем точка 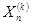заменяется на точку 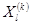, и так же переходим к пункту 2

· Если 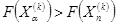, то все векторы 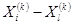уменьшаются в 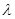раз:

Номер вершины.

Затем возвращаемся к пункту 1.

Правило остановки: