Задания для самостоятельной работы. 1. Случайная величина X задана функцией распределения

1. Случайная величина X задана функцией распределения

.

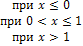Найти вероятность того, что в результате четырех независимых испытаний величина X ровно три раза примет значение, принадлежащее интервалу (0,25; 0,75).

2. Заданы математическое ожидание, а=10 и среднее квадратическое отклонение 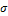=4 нормально распределенной случайной величины X. Требуется найти: а) вероятность того, что X примет значение, принадлежащее интервалу 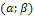, где =8, =20; б) вероятность того, что абсолютная величина отклонения «Х- а» окажется меньше =8.

3. Случайная величина X задана функцией распределения

.

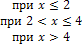Найти вероятность того, что в результате испытания величина X примет значение: а) меньшее 0,2; б) меньшее трех; в) не меньшее трех; г) не меньшее пяти.

4. Дискретная случайная величина задана законом распределения

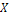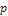	0,2	0,1	0,4	0,3

Найти функцию распределения и построить ее график.

Вопросы для самоконтроля:

1. Как задается нормальный закон распределения непрерывной случайной величины? В чем смысл его параметров?

2. Каковы особенности нормального закона распределения? Поясните их на кривой Гаусса.

3. Как находится вероятность попадания нормально распределённой случайной величины заданный промежуток?

4. Как находится вероятность заданного отклонения нормально распределённой случайной величины от её математического ожидания?