Алгоритм факторизации Ленстры на основе эллиптических кривых

Пусть n – составное число. Время разложения зависит от размера наименьшего делителя: n=p*q. Если p<<q, то найдено будет достаточно быстро.

Алгоритм хорошо распараллеливается и зависит от гладкости количества точек на выбранной кривой.

Суть алгоритма Ленстры заключается в выборе на псевдокривой EC(Z_n) произвольной базовой точки P₀ и домножении ее на всевозможные простые числа и их степени пока не получим kP₀ = ∞ (mod p) ^(*), где p–один из делителей n.

#EC – число точек: занимает интервал [p + 1 -2√p, p + 1 + 2√p].

Алгоритм:

Z_n – основное множество для координат точек эллиптической кривой EC(Z_n) : y²= x³ + ax + b, 0< a,b <p.

Инициализация: //этого в лекциях не было

1. Выберем некоторое значение B₁ , например, B₁ = 10000.

2. Выберем случайным образом числа x, y, a из [0, n − 1] .

3. Вычислим b = y²−x³−ax mod n и g = НОД(n, 4a³+27b²). Если

g = n, возвращаемся к п.2. Если 1 < g < n, тогда прекратим вычисление –

делитель найден. Иначе, определим кривую E : y²= x³+ ax + b и базовую

точку-генератор P₀(x, y).

4. Присвоим изменяемому параметру P(x, y) начальное значение, равное P₀ .

Вычисление:

С = p₁^k1 * p₂^k2 * … * p_t^kt – разложение по простым делителям.

r=max p_i^ki (i<t) – степень гладкости, причём p^r < B_1.

Берём произвольную точку P= P₀ и вычисляем:

P₁= ∏ p_i^ti · P , где p_i^ti < B₁,

в результате чего точка P домножится на p^r.

Продолжим вычисление до тех пор, пока не будут пройдены все простые числа, меньшие B₁ , или не найдется шаг, на котором выполнится условие

НОД(n, P₁) = d > 1.

Если выполнится последнее условие, то искомый делитель n найден.

Иначе, либо увеличиваем B₁ и повторяем все заново, либо переходим

ко второй стадии алгоритма.

Вторая стадия алгоритма://и этого тоже

На второй стадии алгоритма предполагается, что число точек #EC

на выбранной ЭК имеет лишь один делитель q , превышающий границу 1-й

стадии B₁ .

1. Выберем новую границу B₂ , и выпишем все простые числа из интервала [B₁; B₂] : {q₁, q₂, ..., q_m }.

2. Будем последовательно вычислять точки q₁ ·P, q₂ ·P, q₃ ·P, ... пока

не дойдем до границы B₂ , либо не выполнится условие ^(*).

Дивизоры

Построение отображения Вейля и родственного ему отображения Тейта основано на теории дивизоров (делителей) алгебраических кривых, разработанной Андре Вейлем.

Идея понятия дивизора основана на том наблюдении, что коэффициенты любого полинома можно вычислить с точностью до ненулевого множителя, зная корни этого многочлена и их кратность.

Действительно, если многочлен P(x) имеет своими корнями кратности r_i элементы x_i, то .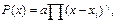

В нашем случае класс изучаемых функций состоит из дробно-рациональных функций над эллиптическими кривыми, т.е. отношений двух многочленов от двух переменных x и y, определенных на точках некоторой эллиптической кривой.

Пусть теперь E : 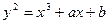–эллиптическая кривая над полем K, а f(x,y) : E → K –дробно-рациональная функция. Если f – не константа, то существует не более конечного числа точек P ∈ E, в которых f(P) = 0 или f(P) = ∞. Точки первого вида называются нулями функции f , а второго –

полюсами f . С точностью до ненулевого множителя функцию f можно задать, перечисляя все ее нули и полюсы и задавая их кратность. Если f имеет нуль (полюс) кратности k в точке P , то f можно представить в виде произведения 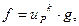, где u_p имеет в точке P нуль (полюс) первого порядка, а 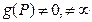Функция u_p называется униформизатором функции f в точке P.

Определение 6.1. Пусть E : 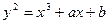– эллиптическая кривая над полем k. Дивизором D над кривой E называется формальная сумма вида ,

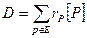в которой коэффициенты r_P – целые числа и число слагаемых с ненулевым коэффициентом r_P

– конечно. Множество точек P , для которых 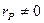, называется носителем (support) дивизора D и обозначается supp(D). Целое число 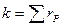P ∈ supp(D), называется степенью D и обозначатся deg(D).

Точка эллиптической кривой, равная 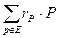, называется суммой дивизора D и обозначается sum(D).

Сумма дивизоров определяется естественным образом. Множество дивизоров эллиптической кривой образует аддитивную группу относительно операции сложения, а нулем является дивизор, у которого все коэффициенты равны 0. В группе дивизоров наиболее важную роль играют дивизоры функций, которые называются главными дивизорами (principal divisors).

Вычислим дивизор прямой l : ax + by + c, проходящей через две заданные точки P1(x1, y1) и P2(x2, y2) эллиптической кривой E. Если l не является касательной в т.P1 и P2, то она пересекает E и в третьей т.P3(x3, y3), а также в бесконечно удаленной точке ∞. В точках P1, P2 и P3 прямая l имеет нули 1 порядка, а в т. ∞ – полюс 3 порядка. Чтобы увидеть это, перепишем уравнение ЭК 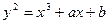в следующем виде:

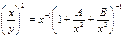(1) откуда 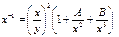(2).

Из уравнения (1) следует, что x/y обращается в 0 в т.∞, а уравнение (2) показывает, что функция x/y является униформизатором в т.∞ и т.∞ является нулем второго порядка для . Значит т.∞ является полюсом 2 порядка для x. Так как y = x · (y/x), то т.∞ является полюсом 3 порядка для y и для функции l = Ax + By + C. Отсюда дивизор прямой l имеет вид 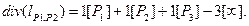(3). Проведем через т.P₃ вертикальную прямую v = x – x₃. Она проходит через т.P₃(x₃, y₃), −P₃(x₃, −y₃) и т.∞, а ее дивизор имеет вид

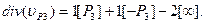. (4)

Из формул (3) и (4) получим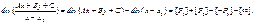

Так как P₁ + P₂ = −P₃ на кривой E, то последнюю формулу можно переписать в виде 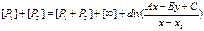(5).

Из формул (3) и (4) можно видеть, что согласно определению 6.1 степени прямых l_P1,P2 и 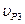равны 0, а их сумма равна ∞, что является примером общего факта, выражаемого следующей теоремой:

Теорема 6.2. Дивизор D эллиптической кривой E, имеющий степень 0, является дивизором некоторой функции тогда и только тогда, когда sum(D) = ∞.

Функции от дивизоров

Отображение, задаваемое формулой (7), является групповым гомоморфизмом из аддитивной группы дивизоров в мультипликативную группу поля K , т.к. f(D₁ + D₂) = f(D₁) · f(D₂), f(D₁ − D₂) = f(D₁)/f(D₂) (6)

Распространяя формулы (6) на произвольные дивизоры, получим формулу 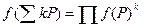(7).

Теорема 6.3.( закона взаимности Вейля) Если f и g – функции на эллиптической кривой такие, что

div(f) и div(g) не имеют общих точек, тогда выполняется следующая

формула: f(div(g)) = g(div(f)).