Ii. способы задания функции

I. Функция, ее область определения.

Пусть дано числовое множество 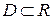; если каждому 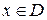поставлено в соответствие по некоторому правилу одно определенное число 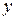, то говорят, что на множестве 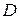определена числовая функция .

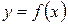Переменная 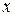называется независимой переменной или аргументом функции, а 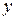- зависимой переменной. Буква f в обозначении функции характеризует именно то правило, по которому получается значение y, соответствующее x.

В данном определении каждому x соответствует единственное значение y, такая функция называется однозначной. Если допустить, чтобы каждому x соответствовало несколько значений y, то функцию называют многозначной. Примером однозначной функции является связь между координатами точки, перемещающейся по прямой линии на плоскости, а примером многозначной функции - связь между координатами точки, перемещающейся по окружности или эллипсу.

Множество D называют областью определения функции. Число y₀, соответствующее значению аргумента 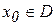, называют значением функции при x = x 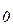и пишут .

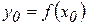Совокупность всех значений, которые принимает функция на области определения, называют множеством значений функции E.

II. Способы задания функции.

Существуют три способа задания функции: аналитический, табличный и графический.

При аналитическом способе задания функция определяется с помощью формулы, по которой вычисляется значение функции при любом значении аргумента из области определения. Наприме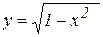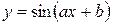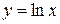р, , , и др.

Каждое аналитическое выражение, содержащее аргумент x, имеет естественную область определения, то есть множество всех тех значений x, для которых оно имеет смысл, то есть вполне определенное, конечное, вещественное значение. Так, функция 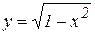имеет естественную область определения при 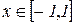, а для функции .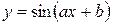

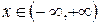Некоторые функции определяются различными формулами при различных значениях аргумента, например,

.

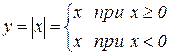При табличном способе задания заданы конкретные значения функции при определенных, наперед заданных значениях аргумента. Такой способ задания обычно связан с экспериментально устанавливаемыми зависимостями между переменными величинами. Его неудобство состоит в том, что функция определена лишь для некоторых значений аргумента. Отыскание значений функции для промежуточных значений аргумента называется интерполяцией.

При графическом способе задания соответствие между аргументом и функцией представлено с помощью рисунка, что позволяет иметь наглядное представление о поведении связанных функциональной зависимостью величин.

Все три способа задания функции связаны между собой. Так, имея аналитическое выражение для функции, можно получить таблицу ее значений и график функции - кривую, для которой координаты точки связаны соотношением. Решение обратной задачи - получение аналитического выражения для функции по таблице или графику - достаточно сложно и рассматривается в специальных разделах математики.