Дифференциальное уравнение типа

Quot;ВХОД-ВЫХОД" ДЛЯ ЧЕТЫРЕХПОЛЮСНИКА

Линейный четырехполюсник п-го порядка сложности описывается в общем случае интегро-дифференциальными уравнениями. Дифференцируя их, можно получить некоторую систему дифференциальных уравнений вида

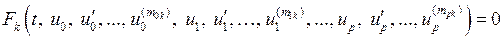, (1.10)

,

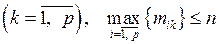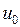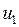где (в соответствии с принятыми нами обозначениями) и – сигналы на входе и выходе четырехполюсника; 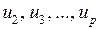– промежуточные сигналы, действующие внутри четырехполюсника.

Во множестве случаев удается разрешить систему (1.10) относительно 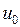и 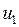, последовательно исключая промежуточные переменные из уравнений. В итоге получается единственное дифференциальное уравнение n-го порядка типа "вход-выход"

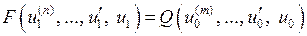. (1.11)

Уравнение типа "вход-выход" в теории электрических систем играет существенную роль. В связи с этим рассмотрим его свойства более подробно.

1.6. СОСТАВЛЕНИЕ УРАВНЕНИЙ ТИПА "ВХОД-ВЫХОД"

ДЛЯ ЧЕТЫРЕХПОЛЮСНИКОВ

1.6.1. ИСПОЛЬЗОВАНИЕ ЗАКОНОВ КИРХГОФА

Для получения уравнений выполняются следующие шаги:

1. Определяется число уравнений, составляемых по первому и второму законам Кирхгофа. Пусть 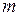– число ветвей схемы (включая ветви со входным источником 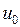и выходным сигналом 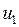), 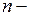число узлов. Тогда число уравнений по первому закону Кирхгофа равно 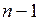, а по второму закону 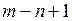. Общее число независимых уравнений .

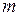2. Выбираются независимые контуры; составляются уравнения по законам Кирхгофа.

3. К полученной системе добавляются динамические уравнения элементов.

4. Путем исключения переменных получают необходимое дифференциальное уравнение типа "вход-выход".

Пример 1.2. Найти дифференциальное уравнение четырехполюсника, представленного на рис. 1.7.

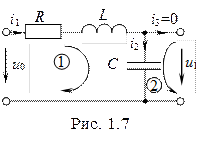Число ветвей данного четырехполюсника 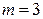, число узлов 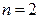. Согласно п. 1 изложенного метода система уравнений будет включать два уравнения по второму закону Кирхгофа

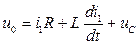, (1.12)

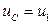, (1.13)

и одно уравнение по первому закону Кирхгофа

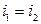. (1.14)

Добавим к системе динамическое уравнение емкости

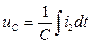. (1.15)

Подставим (1.13) в (1.12)

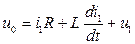. (1.16)

Решим совместно (1.13) и (1.15)

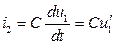. (1.17)

Учитывая (1.14) и (1.17), из (1.16) получим искомое уравнение типа "вход-выход"

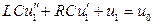. (1.18)

1.6.2. МЕТОД УЗЛОВЫХ ПОТЕНЦИАЛОВ

Метод заключается в выполнении следующих шагов:

1. Выбирается базовый узел. Уравнения получаются наиболее простыми, если выбранный базовый узел является общим для входного и выходного сигнала или наибольшего числа ветвей.

2. В схеме размечаются узлы (здесь – точки соединения двух и более элементов) и для каждого из них составляется уравнение по первому закону Кирхгофа. При этом из двух узлов, к которым подключается источник напряжения, следует обозначать только один (если один из них является базовым, то другой не обозначается вовсе).

3. Токи выражаются через разности потенциалов отмеченных узлов. Число уравнений цепи, составленных таким образом, будет равно числу выделенных узлов.

4. Путем исключения переменных получают необходимое дифференциальное уравнение типа "вход-выход".

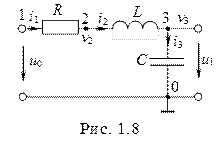Пример 1.3. По методу узловых потенциалов составить дифференциальное уравнение четырехполюсника, приведенного на рис. 1.8.

Примем за базовый узел с номером 0: он является общим для входного и выходного сигналов.

Выделим два узла: 2 и 3. Узел 1 по правилу 2 при составлении уравнений не учитываем. Запишем для выделенных узлов уравнения по законам Кирхгофа

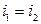, (узел 2)

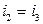. (узел 3)

Выразим токи через разности потенциалов

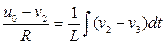, (1.19)

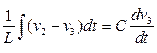. (1.20)

Подставим (1.20) в (1.19) и, учитывая, что 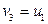, получим

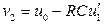. (1.21)

Совместное решение (1.20) и (1.21) дает уравнение (1.18).

1.6.3. МЕТОД ПЕРЕМЕННЫХ СОСТОЯНИЯ

Алгоритм составления уравнений по методу переменных состояния* следующий:

1. Каждая индуктивность 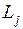и емкость 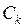заменяются соответственно на источник тока 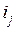и источник напряжения 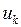. Их направления совпадают с положительными направлениями токов и напряжений в этих элементах.

2. В полученной ветви определяются напряжения 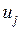на зажимах источников тока 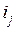и токи 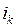в источниках напряжения .

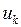3. Производится замена

,

.

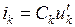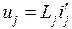4. Путем исключения переменных получают необходимое дифференциальное уравнение типа "вход-выход".

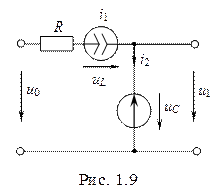Пример 1.4. По методу переменных состояния составить уравнения цепи рис. 1.8.

1. Заменяя в схеме рис. 1.8 индуктивности на источники тока, а емкости на источники напряжения, получаем схему, представленную на рис. 1.9.

2. Определим напряжение 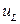и ток 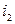источников

,

.

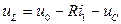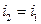3. Заменим 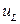и 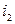на динамические уравнения

,

.

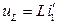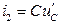Тогда получим следующую систему дифференциальных уравнений, записанных в форме Коши (с выделением в левой части каждого уравнения одной единственной производной):

(1.22) (1.23)

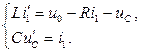
Учитывая, что 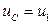, из уравнений (1.22) и (1.23), получим уравнение (1.18).

Примечание. Все изложенные методы на третьем шаге дают систему дифференциальных уравнений, но только метод переменных состояния дает систему в форме Коши. Поэтому метод переменных состояния предпочтителен при составлении системы уравнений четырехполюсника.