Доказать необходимое и достаточное условие того, что данное число 8 меньше корней квадратного уравнения

- Доказать необходимое и достаточное условие того, что данное число 8 располагается между корнями квадратного уравнения.

- Доказать необходимое и достаточное условие того, что данное число 8 больше корней квадратного уравнения.

- Доказать необходимое и достаточное условие того, что данное число 8 совпадает с меньшим (большим) корнем квадратного уравнения.

f(l)\А<0

система: f(l)\А>0; х_в-l>0 (больше)

система: f(l)\А>0; х_в-l<0 (меньше)

система: f(l)\А=0; х_в-l>0 (совпадает с большим)

система: f(l)\А=0; х_в-l<0 (совпадает с меньшим)

Доказывается банально через рисунки (4 параболы). И ко всем условиям надо не забывать дискриминант больше либо равен нуля.

Комплексные числа.

Комплексная плоскость. Действия над комплексными числами в декартовой форме.

С помощью базисных векторов задаются целая и мнимая части комплексного числа.

Суммой двух комплексных чисел z₁ и z₂ называют комплексное число z=(x₁+x₂)+i(y₁+y₂). Другими словами для нахождения суммы двух комплексных чисел необходимо сложить их действительные и мнимые части. Сумма двух комплексно-сопряжённых чисел есть всегда действительное число равное их удвоенной действительной части.

Для нахождения разности комплексных чисел необходимо вычесть отдельно их действительные и мнимые части.

Произведением двух комплексных чисел z₁ и z₂ называют комплексное число

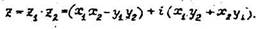
68) Комплексно-сопряжённые числа. Теоремы о сопряжённости суммы и произведения комплексно-сопряжённых чисел.

Два комплексных числа называют комплексно сопряженными, если они имеют одну и ту же действительную часть и взаимно противоположные мнимые части.

Число, сопряжённое с суммой комплексных чисел есть сумма чисел сопряжённых слагаемым.

Число, сопряжённое с произведением двух комплексных чисел есть произведение чисел, сопряжённых с сомножителями.

Теория многочленов.

Действия над многочленами. График многочлена. Алгоритм деления многочленов с остатком (алгоритм Евклида).

При сложении многочленов складывают коэффициенты при одинаковых степенях переменной. Для сложения многочленов существует однозначно определённая обратная операция – вычитание многочленов. При умножении многочленов перемножают каждый одночлен первого сомножителя на каждый одночлен второго, затем приводят подобные члены.

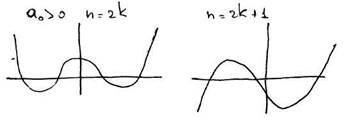
Вот так примерно выглядит график многочлена.

Алгоритм Евклида это деление столбиком.

Теорема Безу. Следствия.

Остаток от деления многочлена на (х-α) равен значению многочлена при х=α.

Действительно, в соответствии с алгоритмом деления с остатком многочлена произвольной степени на многочлен первой степени имеем P_n(x)=(x- α)q_n-1(x)+R₀. Здесь остаток R₀ либо нуль, либо какое-либо число (многочлен нулевой степени), подставляя в это равенство х=α, получаем P_n(α)=( α- α)q_n-1(α)+R₀ à R₀=P_n(α)

Следствие 1: Если число α является корнем многочлена P_n(x), то этот многочлен без остатка делится на линейный двучлен (x- α)

Следствие 2: Если α₁ и α₂ различные корни многочлена P_n(x), то многочлен делится на квадратный трёхчлен ((x- α₁) (x- α₂)).

Следствие 3: Если α₁, α₂…α_k – попарно различные корни многочлена P_n(x), то этот многочлен без остатка делится на многочлен k-ой степени ((x- α₁) (x- α₂)…(x- α_k))