Давление в движущихся жидкостях и газах.
Уравнение Бернулли.
Как следует из уравнения неразрывности, при переходе жидкости с участка трубы с большим сечением на участок с меньшим сечением скорость течения возрастает, т. е. жидкость движется по трубе с переменным сечением с ускорением. Это означает, что на жидкость действует сила. Давление, возникающее в результате действия этой силы, таким образом, зависит от скорости жидкости.
Рассмотрим ламинарное стационарное течение идеальной жидкости в трубке тока, изображенной на рисунке 5.4.1.
Обозначим площадь поперечного сечения, давление и модуль скорости в широкой части трубки, (которой соответствуют сечения 1 и 1¢) через S1, p1 и v1 соответственно, а в узкой части (сечения 2 и 2¢) – через S2, p2 и v2.
За малый интервал времени Dt масса жидкости, занимавшая объём между сечениями 1 и 2 оказалась в объёме между сечениями 1¢ и 2¢, что эквивалентно перемещению массы жидкости 
, заключенной между сечениями 1 и 1¢ в положение между сечениями 2 и 2¢.
Рис. 5.4.1.
, (5.4.1)
где r - плотность жидкости,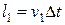 
, 
.
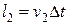Выделенная масса жидкости перемещается под действием сил давления 
и 
и силы тяжести 
. Эти силы совершают работу
, (5.4.2)
, (5.4.3)
. (5.4.4)
Пользуясь законом изменения кинетической энергии
, (5.4.5)
получим
, Þ
, Þ
.
В результате получим уравнение, которое называется уравнением Бернулли.
. (5.4.6)
Из него следует закон Бернулли, который гласит, что полное давление стационарно текущей идеальной жидкости, описываемое формулой,
. (5.4.7)
остается неизменным вдоль всей лини тока.
Полное давление движущейся жидкости, вычисляющееся по формуле (5.4.7) состоит из трех слагаемых. Первое слагаемое в этой формуле p называется статическим давлением, величина 
- динамическим давлением, величина 
- гидростатическим давлением.
Уравнение Бернулли - форма закона сохранения энергии применительно к установившемуся течению идеальной жидкости. Уравнение хорошо выполняется и для реальных жидкостей, для которых внутреннее трение не очень велико. Это уравнение впервые было опубликовано швейцарским физиком Даниилом Бернулли в 1738 году.
Если движение жидкости происходит в горизонтальной трубе ( 
) уравнение Бернулли принимает вид:
. (5.4.8)
Статическое давление p в жидкости может быть измерено с помощью манометра, перемещающегося вместе с жидкостью. Практически давление в разных сечениях трубы измеряется с помощью манометрических трубок, вставленных через боковые стенки в поток жидкости, так чтобы нижние концы трубок были параллельны скоростям частиц жидкости (рис. 5.4.2).
Рис. 5.4.2.
Из уравнения неразрывности следует, что при течении жидкости по трубе, изображенной на рис. 5,4.2, скорость жидкости в широком сечении меньше, чем в узком: 
. Соответственно из уравнения Бернулли (5.4.8) следует, что давления жидкости в соответствующих сечениях 
, т.е уровни жидкости в манометрических трубках 
.
Статическое давление в жидкости, текущей по горизонтальной трубе переменного сечения, больше в тех сечениях потока, в которых скорость ее движения меньше, (а сечение соответственно больше), и наоборот, давление меньше в тех сечениях, в которых скорость больше (сечение меньше).