Теоретический материал. Что такое условие прочности по допускаемому напряжению?

Что такое условие прочности по допускаемому напряжению?

В условиях кручения в поперечных сечениях стержневой конструкции возникают касательные напряжения под действием внутреннего крутящего момента, которые в опасных точках сечения вычисляются по следующей формуле: 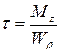, где М_z – величина внутреннего крутящего момента в данном сечении, W_ρ – полярный момент сопротивления – геометрическая характеристика поперечного сечения. Для круглого сечения c диаметром d полярный момент сопротивления 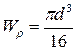. Условием прочности по допускаемому напряжению при кручении считается выполнение следующего неравенства:

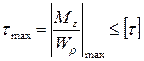
где [τ] – величина допускаемого напряжения, являющаяся справочной величиной или определяемая по характеристикам прочности для данной марки материала как: 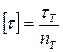для пластичного материала или 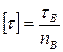для хрупкого материала, где τ_T – предел текучести, τ_В – предел прочности данной марки материала; n_T – коэффициент запаса по текучести, n_В – коэффициент запаса по прочности.

Алгоритм расчета на прочность

1. Определить положение опасного сечения:

· Построить эпюру крутящего момента M_z

· Определить величину максимального касательного напряжения:

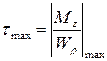
2. Записать условие прочности: 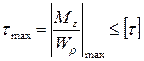и решить его соответственно поставленной задаче.

Какие перемещения испытывают круглые поперечные сечения стержня при кручении?

Согласно гипотезе Бернулли круглые и плоские поперечные сечения стержня до приложения крутящего момента остаются круглыми и плоскими и после его воздействия, поворачиваясь при этом вокруг продольной оси на некоторый угол. Таким образом, перемещением при кручении считается φ – угол закручивания поперечных сечений вокруг продольной оси стержня.

Чтобы оценить деформацию стержня при кручении рекомендуется построить эпюру распределения углов закручивания φ вдоль оси конструкции.

Алгоритм построения эпюры углов закручивания.

1. Выбрать начало координат для отсчета перемещений поперечных сечений (если стержень имеет жесткую заделку, то рекомендуется принять начало координат в заделке).

2. Разделить стержень на участки, в пределах каждого из которых неизменны функция крутящего момента и размер поперечного сечения.

3. Начиная от начала координат, определить абсолютную деформацию каждого участка 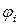(угол закручивания граничных сечений данного участка относительно друг друга) с учетом знака крутящего момента:

· для участка без распределенного момента по формуле:

,

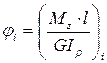где 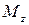– величина крутящего момента данного участка, l – длина участка, G – модуль сдвига (характеристика материала стержня), 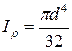– полярный момент инерции круглого сечения;

· для участка с распределенным моментом по формуле:

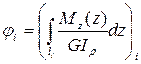
3. Определить перемещение (угол закручивания) каждого граничного сечения стержня относительно выбранного начала координат как накопленную сумму абсолютных деформаций участков, предшествующих данному сечению: .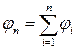

4. По значениям полученных перемещений построить эпюру 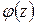, откладывая на базе, параллельной продольной оси стержня, величины углов закручивания в соответствующих сечениях стержня (учитывать, что на участках без распределенного момента функция 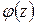изменяется по линейному закону, а на участках с распределенным моментом – по параболическому).

Что такое условие жесткости при кручении?

Условие жесткости при кручении принято записывать либо в абсолютных, либо в относительных (погонных) углах закручивания. Погонным углом закручивания i-го участка стержня называется величина .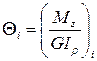

Под условием жесткости, записанным в абсолютных углах закручивания, понимается ограничение максимального угла закручивания сечений стержневой конструкции в результате деформации кручения величиной допускаемого перемещения:

,

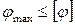где 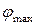– величина максимального угла закручивания сечений вала, 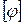– допускаемый угол закручивания, обычно назначаемый из условий эксплуатации или регламентирующими документами.

Под условием жесткости, записанным в относительных углах закручивания, понимается ограничение максимального относительного (погонного) угла закручивания участков стержневой конструкции в результате деформации кручения некоторой допускаемой величиной:

,

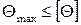где 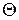_max – величина максимального погонного угла закручивания граничных сечений участков, [ 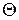] – допускаемый погонный угол закручивания.

Алгоритм расчета на жесткость по абсолютным углам закручивания.

1. Построить эпюру углов закручивания 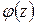согласно приведенному выше алгоритму.

2. По эпюре определить максимальный по абсолютной величине угол закручивания, подставить в условие жесткости: 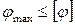и сделать вывод о его выполнении.

Алгоритм расчета на жесткость по относительным углам закручивания.

1. Найти погонные углы закручивания для каждого участка стержня по формуле: .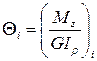

2. Определить максимальный по абсолютной величине погонный угол закручивания: 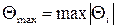, подставить в условие жесткости: 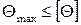и сделать вывод о его выполнении.