Натяжения методом капиллярных волн

Цель работы: изучение влияния поверхностно-активных веществ (ПАВ) на поверхностное натяжение жидкости, определение зависимости коэффициента поверхностного натяжения водных растворов от концентрации ПАВ и измерение концентрации ПАВ методом капиллярных волн.

Приборы и материалы: генератор капиллярных волн на поверхности воды, дистиллированная вода, водные растворы с различными концентрациями ПАВ, лист белой бумаги и линейка.

Теоретические сведения

1. Свойства жидкостей. Поверхностное натяжение.

Жидкость это агрегатное состояние вещества, промежуточное между газообразным и кристаллическим состояниями. Поэтому она обладает свойствами как газа, так и кристаллического вещества. Молекулы газа слабо связаны между собой силами межмолекулярного взаимодействия и средняя кинетическая энергия теплового движения молекул газа значительно превосходит среднюю потенциальную энергию их взаимодействия, обусловленную силами притяжения между ними. Вследствие чего молекулы газа разлетаются в разные стороны и газ занимает предоставленный ему объем. В твердых и жидких веществах силы притяжения между молекулами уже существенны и они удерживают молекулы на определенных расстояниях. Причем средняя кинетическая энергия теплового движения молекул меньше средней потенциальной энергии их взаимодействия, обусловленной силами притяжения между ними. Поэтому твердые тела и жидкости имеют определенный объем.

В газах молекулы движутся хаотично и нет никакой закономерности в их взаимном расположении. Рентгеноструктурный анализ жидкостей показал, что характер расположения молекул жидкостей промежуточен между газом и кристаллическим веществом. В пространственном расположении молекул жидкости наблюдается так называемый ближний порядок. Это означает, что по отношению к любой молекулы расположение ближайших к ней соседних молекул является упорядоченным. Однако по мере удаления от данной молекулы расположение по отношению к ней других молекул становится все менее упорядоченным, и довольно быстро порядок в расположении молекул полностью исчезает. В кристаллах присутствует дальний порядок: упорядоченное расположение молекул по отношению к любой молекулы наблюдается в пределах значительного объема.

Согласно теории российского физика Я.И.Френкеля тепловое движение молекул в жидкости является результатом того, что каждая молекула в течение некоторого времени колеблется около определенного положения равновесия, после чего она скачком переходит в новое положение, отстоящее от исходного на расстоянии порядка межмолекулярного. Таким образом, молекулы довольно медленно перемещаются в объеме жидкости и диффузия молекул происходит гораздо медленнее, чем в газах. С повышением температуры жидкости увеличиваются частоты колебательного движения и кинетические энергии молекул, возрастает подвижность молекул, что, в свою очередь, является причиной уменьшения вязкости жидкости.

На каждую молекулу жидкости со стороны окружающих молекул действуют силы притяжения, быстро убывающие с увеличением расстояния. Начиная с некоторого минимального расстояния силами притяжения между молекулами можно пренебречь. Это расстояние (порядка 10^{-9 м) называется радиусом молекулярного действия} r, а сфера радиуса r– сферой молекулярного действия.

Выделим внутри жидкости какую-либо молекулу m и проведем вокруг нее сферу радиуса r(рис. 11.1). Эта молекула испытывает притяжение со стороны всех соседних с ней молекул, находящихся в пределах сферы молекулярного действия. Очевидно, равнодействующая всех сил притяжения для молекулы m, находящейся от поверхности жидкости на расстоянии, превышающим r, в среднем равна нулю. Ситуация кардинально меняется, если молекула, например молекула n, расположена от поверхности на расстоянии, меньшем r. В данном случае сфера молекулярного действия лишь частично расположена внутри жидкости. Поскольку концентрации молекул газа и пара в слое, расположенном над поверхностью жидкости, мала по сравнению с концентрацией молекул в жидкости, то равнодействующая сил F, приложенных к каждой молекулы поверхностного слоя, не равна нулю и направлена внутрь жидкости. Таким образом, результирующие силы всех молекул поверхностного слоя оказывают на жидкость давление, называемое молекулярным (или внутренним). Молекулярное давление не действует на тело, помещенное в жидкость, так как оно обусловлено силами, действующими только между молекулами самой жидкости.

Полная механическая энергия молекул жидкости складывается из кинетической энергии (колебательного, вращательного и поступательного движений) и потенциальной энергии, обусловленной силами межмолекулярного взаимодействия. При переходе молекулы из глубины жидкости в поверхностный слой совершается работа против сил, действующих в поверхностном слое жидкости. Эта работа совершается молекулой за счет уменьшения ее кинетической энергии и расходуется на повышение потенциальной энергии молекулы. Средние кинетические энергии молекул в поверхностном слое и внутреннем объеме жидкости, имеющих одинаковые температуры, равны, но молекулы поверхностного слоя жидкости обладают большей потенциальной энергией, чем молекулы внутри жидкости. Эта дополнительная энергия, которой обладают молекулы в поверхностном слое жидкости, называемая поверхностной энергией, пропорциональна площади этого слоя ΔS:

ΔE=σΔS, (11.1)

где σ– коэффициент поверхностного натяжения.

Отсюда

σ= ΔE/ΔS, (11.2)

т.е. коэффициент поверхностного натяжения численно равен энергии, которую необходимо затратить, чтобы создать единицу площади поверхности жидкости. Единица измерения коэффициента поверхностного натяжения – джоуль на квадратный метр (Дж/м²).

Так как равновесное состояние характеризуется минимумом потенциальной энергии, то при отсутствии внешних сил жидкость будет принимать такую форму, чтобы при определенном объеме она имела минимальную поверхность, т.е. форму шара. В условиях невесомости капля любой жидкости, независимо от ее размеров, имеет сферическую форму, что наблюдается на околоземных космических станциях.

Итак, условием устойчивого равновесия жидкости является минимум поверхностной энергии. Отсюда следует, что жидкость при заданном объеме должна иметь наименьшую площадь поверхности, т.е. жидкость стремиться сократить площадь свободной поверхности. В этом случае поверхностный слой жидкости можно рассматривать как растянутую упругую пленку, в которой действуют силы натяжения.

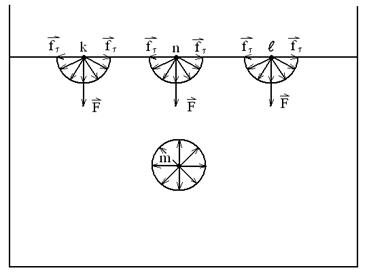
Рис. 11.1

Вернемся к рисунку 11.1. Хотя равнодействующая сил F, приложенных к каждой молекуле поверхностного слоя, направлена внутрь жидкости, но между соседними молекулами, например, k и nили n и l, действуют силы притяжения f_τ , направленные вдоль поверхности жидкости. Силы f_τ вызывают стремление жидкости сократить свою поверхность. Они называются силами поверхностного натяжения.

Проделаем такой опыт. На проволочную П-образную рамку (рис.11.2) наденем легкую перекладину, могущую скользить по боковым направляющим рамки, и, погрузив рамку в сосуд с мыльным раствором, затянем рамку мыльной пленкой. Стремясь сократить свою поверхность, мыльная пленка будет поднимать перекладину вверх. Сила поверхностного натяжения, действующая на единицу длины поверхности мыльной пленки, примыкающей к перекладине, равна:

f= F_τ/l , (11.3)

где F_τ – модуль равнодействующей сил поверхностного натяжения, приложенных к перекладине, длиной l.

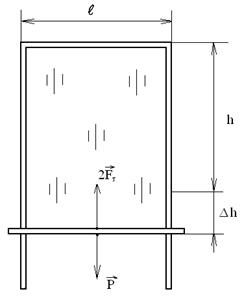
Рис. 11.2

Поскольку мыльная пленка имеет две поверхности, то модуль результирующей силы поверхностного натяжения, направленной вертикально вверх, равен удвоенной силе поверхностного натяжения, действующей со стороны одной поверхности:

2F_τ=2f·l . (11.4)

Чтобы уравновесить силу поверхностного натяжения, к перекладине надо приложить силу P, модуль которой равен

P=2f·l. (11.5)

Пусть сила P была приложена к нерастянутой пленке и до достижения состояния равновесия эта сила совершила положительную работу растяжения

ΔA_P=P·Δh=2f·l·Δh= f·ΔS , (11.6)

где Δh – модуль перемещение перекладины; ΔS=2l·Δh – приращение площади обеих поверхностей пленки. При этом сила поверхностного натяжения совершила отрицательную работу

ΔA=- ΔA_P . (11.7)

Работа силы P расходуется на увеличение поверхностной энергии пленки

ΔA_P=ΔE. (11.8)

Приравнивая правые части равенств (11.1) и (11.6), получаем, что

σ= f , (11.9)

т.е. коэффициент поверхностного натяжения σ численно равен силе поверхностного натяжения, приходящейся на единицу длины контура, ограничивающего поверхность жидкости. Поэтому коэффициент поверхностного натяжения можно измерять в ньютонах на метр (Н/м).

Следует отметить, что в общем случае работа растяжения ΔA_P не равна увеличению поверхностной энергии жидкости ΔE. Внутренняя энергия Uжидкости равна сумме внутренней энергии U_об всего объема жидкостии поверхностной энергии E:

U= U_об+ E. (11.10)

Поэтому изменение внутренней энергии жидкости

ΔU=Δ U_об+ ΔE, (11.11)

где ΔU_об – изменение внутренней энергии всего объема жидкости; ΔE – изменение поверхностной энергии.

Согласно первому закону термодинамики теплота ΔQ, полученная жидкостью, расходуется на увеличение ее внутренней энергии ΔU и совершение работы ΔA жидкости против внешних сил:

ΔQ= ΔU+ ΔA= Δ U_об+ ΔE+ ΔA. (11.12)

При адиабатном растяжении поверхности жидкости (ΔQ=0) справедливо равенство:

-ΔA= Δ U_об+ ΔE. (11.13)

Поскольку положительная работа силы растяжения ΔA_P=- ΔA, то

ΔA_P= Δ U_об+ ΔE. (11.14)

При увеличении площади поверхности жидкости дополнительное количество молекул перемещается из глубины жидкости в поверхностный слой, теряя при этом кинетическую энергию. В результате чего температура жидкости и внутренняя энергия Δ U_об всего объема жидкости понижаются, т.е.

Δ U_об<0. (11.15)

Из равенства (11.13) следует, что

ΔA_P< ΔE. (11.16)

При медленном растяжении температура жидкости остается неизменной за счет притока теплоты ΔQ извне. В этом случае процесс растяжения жидкости является изотермическим и изменение внутренней энергии ΔU_об всего объема жидкости равно нулю. Уравнение первого закона термодинамики принимает вид:

ΔQ= ΔE+ ΔA= ΔE- ΔA_P. (11.17)

Отсюда получаем

ΔA_P= ΔE+ ΔQ. (11.18)

Поскольку ΔQ>0, то

ΔA_P>ΔE. (11.19)

Считая, что количество теплоты ΔQ, полученное жидкостью в процессе ее растяжения, незначительно можно записать

ΔA_P ≈ΔE. (11.20)

2. Поверхностно-активные вещества. Адсорбция.

При растворении твердого или жидкого вещества в жидком растворителе силы притяжения между молекулами растворенного вещества и растворителя обычно не равны силам взаимного притяжения между молекулами чистого растворителя. Рассмотрим случай, когда силы притяжения между молекулами растворенного вещества и растворителя меньше сил притяжения между молекулами растворителя. Такие растворенные вещества называются поверхностно-активными (ПАВ). При растворении в воде к этим веществам принадлежат мыло, ряд жирных кислот и многие другие. Так как молекулы растворенного вещества притягиваются молекулами растворителя слабее, чем молекулы самого растворителя, то из поверхностного слоя внутрь жидкости преимущественно втягиваются молекулы растворителя и в поверхностном слое увеличивается концентрация растворенного вещества, уменьшая тем самым поверхностное натяжение раствора. Равновесие наступает тогда, когда число молекул растворенного вещества, втягиваемых из поверхностного слоя в глубь жидкости, будет равняться числу молекул, приходящих вследствие диффузии из глубинных слоев жидкости на поверхность. Поверхностный слой оказывается обедненным молекулами растворителя и обогащенным молекулами растворенного вещества. Это явление носит название адсорбции. Им объясняется устойчивость жидких пленок, пены и т.д.

Пленка из чистой жидкости неустойчива при действии постоянной силы: она либо сжимается, если приложенная сила меньше сил поверхностного натяжения, либо растягивается, если приложенная сила больше сил поверхностного натяжения. При растворении поверхностно-активного вещества, например, мыла, его молекулы концентрируются в поверхностном слое растворителя, понижая поверхностное натяжение. При растяжении такой пленки ее поверхность увеличивается и часть растворенного вещества из остального объема жидкости переходит на новую поверхность. Этот процесс вызывает уменьшение концентрации растворенного вещества на остальной поверхности пленки и, следовательно, увеличение ее поверхностного натяжения. Чем сильнее растягивается пленка, тем больше становится поверхностное натяжение. При сокращении пленки имеет место обратный процесс. Таким образом, пленка раствора поверхностно-активного вещества ведет себя подобно упругой пленке и является устойчивой. Аналогично объясняется устойчивость пены.

3. Определение коэффициента поверхностного натяжения методом капиллярных волн.

Коэффициент поверхностного натяжения σ воды является важным параметром, оказывающим существенное влияние на экологическую обстановку в природе. Наличие примесей, среди которых могут оказаться и поверхностно-активные вещества (ПАВ), может оказывать существенное влияние на коэффициент поверхностного натяжения.

Все используемые методы определения σ имеют тот недостаток, что при измерениях используется взаимодействие жидкости с поверхностями твердых тел, состояние поверхности которых может существенно влиять на получаемый результат.

В методе определения коэффициента поверхностного натяжения с использованием капиллярных волн нет взаимодействия жидкости с поверхностями твердых тел и, поэтому он может быть использован в экологических исследованиях.

Цель данной работы - научиться использовать метод капиллярных волн для измерения коэффициента поверхностного натяжения и определения концентрации алкилсульфаната натрия (ПАВ) в воде.

Волны на поверхности жидкости являются одним из самых сложных и интересных явлений, происходящих в природе. При этом картина наблюдаемых явлений существенным образом зависит от параметров жидкости и длины волны.

При распространении поверхностной волны существенное влияние оказывают два фактора: сила тяжести и сила поверхностного натяжения. Общая картина достаточно сложная, однако, в некоторых случаях задача решаема. Критерием, определяющим характер волновых процессов на поверхности, будем считать потенциальную энергию волны.

Энергию, которой обладают поверхностные волны, можно разделить на два вида: гравитационная и энергия поверхностного натяжения. Гравитационная энергия E_гр - потенциальная энергия поднимаемой массы воды при волновом движении. Энергия поверхностного натяжения E- это энергия, обусловленная искривлением поверхности воды при волновом движении.

Общее уравнение плоской поверхностной волны, распространяющейся вдоль оси x(z - вертикальная ось), в приближении малых амплитуд, можно записать:

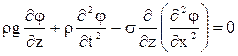. (11.21)

где 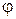= 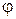_(x,z,t) – потенциал скоростей частиц жидкости.

Решение этого уравнения будем искать в виде

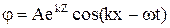, (11.22)

где k = 2π/λ - волновое число, λ- длина волны, ω- циклическая частота.

Непосредственной подстановкой решения (11.22) в (11.21) получим уравнение, связывающее ω и k(дисперсионное отношение):

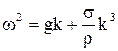, (11.23)

гдеg-ускорение свободного падения, ρ- плотность жидкости.

Для больших длин волн, когда выполняется условие k<<(gρ⁄2σ)^1/2, можно пренебречь влиянием поверхностного натяжения.Практика показывает, что для воды при нормальной температуре это условие выполняется при длинах волн λ>1 м (для воды (gρ⁄2σ)^1/2 ≈ 260 м^-1). В этом случае E_гр>>E и волна является чисто гравитационной.

Для коротких длин волн, распространяющихся на поверхности воды, когда k >>(gρ⁄2σ)^1/2 при λ<3см , E >> E_гр и наблюдается чисто капиллярная волна. При этом справедливо равенство:

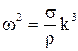, (11.24)

где σ - коэффициент поверхностного натяжения, ρ - плотность воды. В промежуточных случаях имеют место гравитационно-капиллярные волны.

Длина капиллярных волн существенным образом зависит от поверхностного натяжения и частоты. Поэтому, измеряя частоту и длину капиллярных волн можно определить коэффициент поверхностного натяжения воды.

Теперь, используя известные соотношения 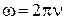(ν – частота) и 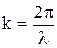, можно получить формулу, связывающую коэффициент поверхностного натяжения с частотой и длиной волны:

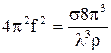. (11.25)

Отсюда следует, что

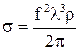. (11.26)

Для определения длины волны используется стробоскопический метод. Если возбудить точечным источником на поверхности воды капиллярные волны, то будут наблюдаться бегущие волны, длину которых определить невозможно. Однако если при этом освещать поверхность воды короткими вспышками света с частотой равной частоте волны, будет наблюдаться стационарная картина и длину волны можно легко измерить.

Описание установки

На рис. 11.3 приведен генератор поверхностных волн:

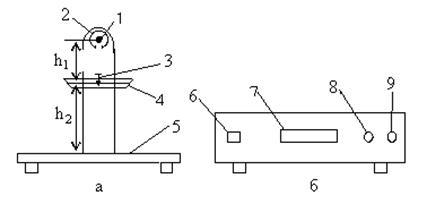
Рис. 11.3.

1 – лампочка, 2 – вращающаяся диафрагма, 3 – вибрирующий шток,

4 – ванна для воды, 5 – столик, 6 – кнопка включения сети,

7 – индикатор, 8 и 9 – ручки изменения частоты вибрации штока.

В данной установке частота световых вспышек совпадает с частотой колебаний штока. Эта частота измеряется встроенным частотомером и регистрируется на индикаторе 7. На столике наблюдается увеличенная картина капиллярных волн. Коэффициент увеличения

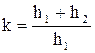= 2,85 , (11.27)

где 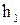- расстояние от нити лампы накаливания до поверхности воды, 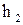- расстояние от поверхности воды до столика.

Порядок выполнения работы

1. Налить дистиллированную воду в ванну (4) до такого уровня, чтобы вибрирующий шток (3) касался поверхности воды.

2. Положить лист белой бумаги на столик (5).

3. Включить генератор в сеть 220 В и нажать кнопку (6). После чего частота вибрации штока устанавливается в диапазоне от 65 до 72 Гц.

4. Наблюдать картину волн в виде концентрических светлых и темных окружностей с центром в точке соприкосновения вибрирующего штока с водой.

5. Установить линейку вдоль радиуса указанных окружностей, отметить центры 11-ти светлых окружностей и измерить длину 10-ти волн.

6. Записать частоту вибрации штока ν.

7. Вычислить измеренную длину 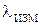волны.

8. Вычислить истинное значение длины волны .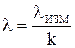

9. Вычислить коэффициент поверхностного натяжения 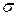дистиллированной воды, используя формулу (11.26).

10. Выключить генератор нажатием на кнопку (6).

11. Зажать пальцами сливную трубку, вынуть из нее пробку и слить воду из ванны в пластиковый стакан.

12. Снять ванну с колонки генератора, приподнимая ее передний край так, чтобы вибрирующий шток не касался дна и края ванны.

13. Слить оставшеюся воду из ванны, вставить пробку в сливную трубку и установить ванну на колонке генератора.

14. Налить водный раствор с известной концентрацией ПАВ (г/л) в ванну.

15. Выполнить п.п. 1-8.

16. Вычислить коэффициент поверхностного натяжения 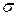водного раствора с известной концентрацией ПАВ (г/л), используя формулу (26).

17. Выполнить п.п. 10-12.

18. Слить оставшеюся водный раствор из ванны, промыть ванну водой, вставить пробку в сливную трубку и установить ванну на колонке генератора.

19. Налить водный раствор с известной концентрацией ПАВ (г/л) в ванну.

20. Выполнить п.п. 1-8, 16, 10-12, 18, 19 еще для двух водных растворов ПАВ.

21. Построить график зависимости коэффициента поверхностного натяжения 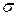(Н/м) водного раствора от концентрации ПАВ (г/л).

22. Налить водный раствор с неизвестной концентрацией ПАВ в ванну (4) до такого уровня, чтобы вибрирующий шток (3) касался поверхности воды.

23. Выполнить п.п. 2-8, 16, 10-12, 18.

24. Определить неизвестную концентрацию ПАВ в водном растворе, используя график зависимости коэффициента поверхностного натяжения 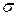(Н/м) водного раствора от концентрации ПАВ (г/л).

Контрольные вопросы

1. Какими физическими свойствами обладают жидкости?

2. Что такое ближний и дальний порядок расположения молекул в веществах?

3. Что такое радиус молекулярного действия?

4. Что такое молекулярное (внутреннее) давление жидкости?

5. Что такое поверхностная энергия жидкости?

6. Как определяется коэффициент поверхностного натяжения?

7. Что такое силы поверхностного натяжения?

8. Каким способом измеряется коэффициент поверхностного натяжения мыльной пленки?

9. Из чего складывается внутренняя энергия жидкости?

10. Какими физическими свойствами обладают поверхностно-активные вещества?

11. Что такое адсорбция?

12. Что собой представляют гравитационные и капиллярные волны на поверхности жидкости?

13. Какая связь существует между коэффициентом поверхностного натяжения, частотой и длиной капиллярной волны?

14. Как измеряется длина капиллярной волны?