Сравнение работы приемника при соединениях треугольником и звездой

Схема соединения «треугольником»

При соединении фазных обмоток источника трехфазного тока «треугольником» (рис. 211, а) конец первой фазы АВ соединяется с началом второй фазы ВС, конец второй фазы соединяется с началом третьей фазы СА и конец третьей фазы — с началом первой АВ. Три линейных провода 1, 2 и 3, идущих к приемникам электрической энергии, присоединяются к началам А, В и С этих фаз. Точно так же могут соединяться и отдельные группы приемников Z_AB, Z_BC, Z_CA (фазы нагрузки). При этом каждая фаза нагрузки присоединяется к двум линейным проводам, идущим от источника, т. е. включается на линейное напряжение, которое одновременно будет и фазным напряжением. Таким образом, в схеме «треугольник» фазные напряжения Uф равны линейным Uл и не зависят от сопротивлений Z_AB, Z_BC, Z_CA фаз нагрузки.

Линейные токи в схеме «треугольник» согласно первому закону Кирхгофа для узлов А, В и С соответственно:

i_A= i_AB– i_CA; i_B= i_BC– i_AB; i_C= i_CA– i_BC

Переходя от мгновенных значений токов к их векторам, получим:

?_A= ?_AB– ?_CA; ?_B= ?_BC– ?_AB; ?_C= ?_CA– ?_BC

Следовательно,линейный ток равен векторной разности соответствующих фазных токов.

По полученным векторным уравнениям можно для равномерной нагрузки фаз построить векторную диаграмму (рис. 211,б), которую можно преобразовать в диаграмму (рис. 211, в), из которой

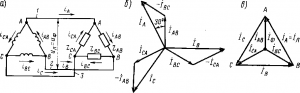Рис. 211. Схема «треугольник» (а) и векторные диаграммы токов для этой схемы при равномерной нагрузке (б и в)

видно, что при равномерной нагрузке фаз векторы линейных токов ?_А, ?_B, ?_C образуют равносторонний треугольник ABC, внутри которого расположена трехлучевая звезда векторов фазных токов ?_АВ, ?_BC и ?_СА. Отсюда по аналогии с диаграммой рис. 207,б следует, что

I_л= 2I_фcos 30° = 2I_ф?3 / 2 = ?3 I_ф

т. е. при равномерной нагрузке фаз в схеме «треугольник» линейный ток больше фазного тока в?3 раз.

Следовательно, при переключении приемников со «звезды» на «треугольник» фазные токи возрастают в ?3 раз, а линейные токи — в 3 раза. Возможность включения одних и тех же приемников по схеме «звезда» или «треугольник» расширяет область их применения. Например, если приемник рассчитан на фазное напряжение 220 В, то при соединении по схеме «треугольник» он может быть включен в сеть с линейным напряжением 220 В, а при соединении по схеме «звезда» — в сеть с линейным напряжением 220?3 = 380 В.

Схема «звезда с нулевым проводом».При соединении фазных обмоток источника трехфазного тока (например, генератора) по схеме «звезда с нулевым проводом» концы его трех обмоток соединяют в общий узел 0, который называется нулевой точкой, илинейтралью источника (рис. 206). Приемники электрической энергии объединяют в три группы Z_A, Z_B и Z_c (фазы нагрузки), концы которых также соединяют в общий узел 0′ (нулевая точка, или нейтраль нагрузки). Обмотки источника соединяют с фазами нагрузки четырьмя проводами. Провода 1, 2 и 3, присоединенные к началам фазных обмоток (А, В, С), называют линейными. Провод 4, соединяющий нулевые точки 0 и 0′, называют нулевым, или нейтральным. Напряжения u_А, u_в и u_с между началами и концами обмоток отдельных фаз источника или фаз нагрузки Z_A, Z_B и Z_c называют фазными. Они равны также напряжениям между каждым из линейных проводов и нулевым проводом. При отсутствии потери напряжения в обмотках источника (при холостом ходе) фазные напряжения равны соответствующим э. д. с. в этих обмотках. Фазными токами i_A, i_B, i_c называют токи, протекающие по обмоткам источника или фазам нагрузки Z_A, Z_B и Z_c. Напряжения u_AB, u_BC, u_CA между линейными проводами и токи, проходящие по этим проводам, называют линейными.

Примем условно за положительное направление токов i_A, i_B и i_c в фазах источника — от конца соответствующей фазы к ее началу,

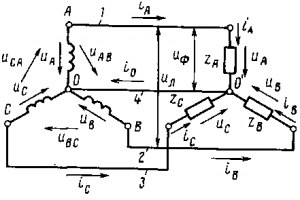Рис. 206. Схема «звезда с нулевым проводом», направление в ней линейных и фазных токов и напряжений

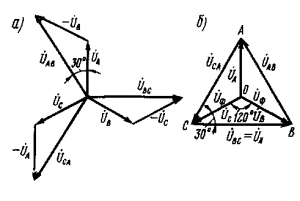Рис. 207. Векторные диаграммы напряжений для схемы «звезда с нулевым проводом»

в фазах нагрузки — от начала к концу, а в линейных проводах — от источника к приемнику. Будем считать положительными напряжения u_А, u_B и u_C в фазах источника и нагрузки, если они направлены от начала фаз к концам, а линейные напряжения u_АВ, u_BC, u_СА — если они направлены от предыдущей фазы к последующей.

Из рис. 206 следует, что в схеме «звезда» линейные токи равны фазным, т. е. I_л = I_ф, так как при переходе от фазы источника или нагрузки к линейному проводу нет каких-либо ответвлений. Мгновенные значения напряжений согласно второму закону Кирхгофа:

u_АВ= u_А– u_B; u_BC= u_B– u_С; u_СА= u_С– u_А.

Переходя от мгновенных значений напряжений к их векторам, имеем:

?_АВ= ?_А– ?_B; ?_BC= ?_B– ?_С; ?_СА= ?_С– ?_А

Схема «звезда без нулевого провода». При равномерной или симметричной нагрузке всех трех фаз, когда во всех фазах включены одинаковые активные и реактивные сопротивления (R_A =R_B = R_Cи Х_A=Х_В=Х_С), фазные токи i_A, i_B и i_C будут равны по величине и сдвинуты от соответствующих фазных напряжений на равные углы. В этом случае получаем симметричную систему токов, при которой токи i_A, i_B, i_C будут сдвинуты по фазе друг относительно друга на угол 120°, а ток i₀ в нулевом проводе в любой момент времени равен нулю (рис. 208,б).

Очевидно, что при равномерной нагрузке можно удалить нулевой провод и передавать электрическую энергию источника к приемнику по трем линейным проводам 1, 2 и 3 (рис. 209). Такая схема называется «звезда без нулевого провода». При трехпровод-ной системе передачи электрической энергии в каждое мгновение ток по одному (или двум) проводу проходит от источника трехфазного тока к приемнику, а по двум другим (или одному) протекает обратно от приемника к источнику (рис. 210). Векторная диаграмма напряжений для схемы «звезда без нулевого провода» при равномерной нагрузке фаз будет такая же, как и для схемы «звезда с нулевым проводом» (см. рис. 207). Такими же будут и соотношения между фазными и линейными токами и напряжениями:

I_л= I_Ф и U_л= ?3 U_Ф

Следует отметить, что схема «звезда без нулевого провода» может быть применена только при равномерной нагрузке фаз. Практически это имеет место лишь при подключении к источникам трехфазного тока электрических двигателей, так как каждый трехфазный электродвигатель снабжен тремя одинаковыми обмотками, которые равномерно нагружают все три фазы. При неравномерной нагрузке напряжения на отдельных фазах нагрузки будут различными. На некоторых фазах (с меньшим сопротивлением) напряжение уменьшится, а на других увеличится по сравнению с нормальным, что является недопустимым.

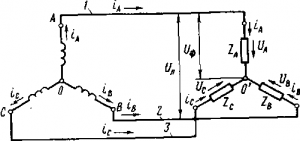Рис. 209. Схема «звезда без нулевого провода»

_.

Магнитные цепи

Под магнитной цепью (МЦ) в электротехнике принято понимать электрическую цепь, содержащую одно или несколько феромагнитных тел, используемую для усиления магнитного поля и образования, вдоль которого замыкается магнитный поток, создаваемый магнитодвижущими силами катушки.

МЦ состоит из следующих элементов: источник магнитодвижущей силы, катушка, подвижный и неподвижный магнитопровод, воздушный зазор. Катушка представляет собой каркас, выполненный из диэлектрика, на который намотан медный провод круглого сечения. В качестве материала для магнитопровода используют сталь и ее сплавы.

Для электромагнитной системы переменного тока применяют магнитомягкие материалы, которые, обладая наиболее узкой петлей гистерезиса, отличаются высокой магнитной проницаемостью. Эти материалы отличаются прямой намагничивания, представляющей собой прямую зависимость магнитной индукции от напряженности магнитного поля.

Для постоянного магнита применяют магнитотвердые материалы, которые, напротив, обладают широкой петлей гистерезиса и характеризующиеся малой магнитной проницаемостью. При расчете МЦ необходимо определить проводимость воздушного зазора.

Её величина прямо пропорциональна сечению объема, по которому, собственно, проходит магнитный поток и обратно пропорциональна длине воздушного зазора в магнитопроводе. Изменяемый при перемещении якоря в магнитопроводе воздушный зазор, называется рабочим воздушным зазором.

Различают следующие виды МЦ: неразветвленные – когда магнитный поток замыкается последовательно и будет одинаков на всех участках этой МЦ и разветвленные – магнитный поток в таких МЦ замыкается по двум и более параллельным магнитопроводам.

39. Разветвленные и неразветвленный магнитные цепи.

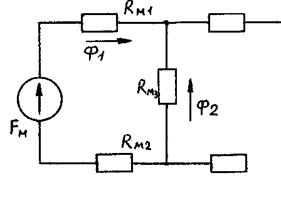
Магнитные цепи можно разделить на неразветвленные и разветвленные. В неразветвленной магнитной цепи магнитный поток Ф одинаков для различных участков цепи. В ней не содержится магнитных узлов, где сходятся несколько магнитных потоков (более двух) (рис. 33,а).

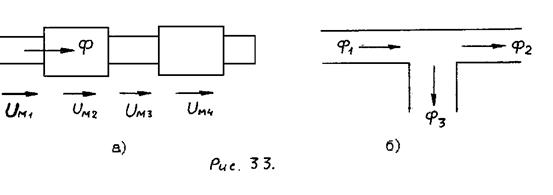
Для последовательной неразветвленной магнитной цепи:

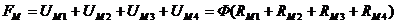
где

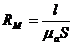
В разветвленной магнитной цепи содержатся узлы, где сходятся несколько магнитных потоков (рис. ,б).

Для узлов разветвленной магнитной цепи справедлив 1-ый закон Кирхгофа для магнитных цепей:

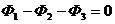
ЗАКОН ПОЛНОГО ТОКА

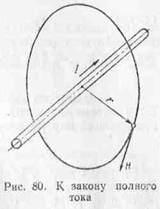
На рис. 80 показан проводник с током I, пронизывающий поверхность, ограниченную замкнутым контуром в виде окружности. Пусть центр окружности лежит на оси проводника. В пространстве, окружающем проводник с током, возникает магнитное поле. Так как отдельные точки контура находятся от проводника на равных расстояниях, то напряженность поля, созданная током в каждой точке контура, будет также одинаковой. Направление вектора напряженности поля Я зависит от направления тока в проводнике и определяется по "правилу буравчика". Вектор Н располагается по касательной к окружности контура.

Путем опытов и расчетов установлено, что произведение напряженности поля Н в точках контура на длину этого контура l равно току I, пронизывающему поверхность, ограниченную данным контуром.

Таким образом,

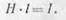
В общем случае поверхность могут пронизывать несколько токов. Тогда определяют так называемый полный ток, т. е. находят алгебраическую сумму токов ( ∑I). Для этого случая можно записать:

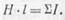
Это выражение носит название закона полного тока Закон полного тока является основным законом при расчете магнитных цепей и дает возможность в некоторых случаях легко определить напряженность поля.