Задачи измерения связи в статистике. Шкалы измерения значений признаков. Корреляция. Коэффициент ковариации.

При исследовании связи между изучаемыми признаками, показателями, процессами, явлениями основными задачами статистики будут:

1) проверка положений теории о возможности связи или выявление наличия новой связи;

2) определение формы связи и исчисление её количественных характеристик (придание выявленной связи аналитической формы зависимости);

3) измерение (количественное выражение) степени тесности связи между отдельными причинами (факторами) и результатом их воздействия.

ШКАЛЫ НАИМЕНОВАНИЙ отражают качественные свойства. Их элементы характеризуются только соотношениями эквивалентности (равенства) и сходства конкретных качественных проявлений свойств. Примерами таких шкал является шкала классификации (оценки) цвета объектов по наименованиям (красный, оранжевый, желтый, зеленый и т.д.), опирающаяся на стандартизованные атласы цветов, систематизированные по сходству.

Шкалы наименований, по существу, качественны; однако возможны некоторые статистические операции при обработке результатов измерений в этих шкалах, например, можно найти модальный или наиболее многочисленный класс эквивалентности.

ШКАЛЫ ПОРЯДКА - описывают свойства, для которых имеют смысл не только соотношения эквивалентности, но и соотношения порядка по возрастанию или убыванию количественного проявления свойства. Характерным примером шкал порядка являются существующие шкалы чисел твердости тел, шкалы баллов землетрясений, шкалы баллов ветра, шкала оценки событий на АЭС и т.п.

В этих шкалах также нет возможности ввести единицы измерений из-за того, что они не только принципиально нелинейны, но и вид нелинейности может быть различен и неизвестен на разных ее участках. Результаты измерений в шкалах твердости, например, выражаются в числах твердости по Бринеллю, Виккерсу, Роквеллу, Шору, а не в единицах измерений. Шкалы порядка допускают монотонные преобразования, в них может быть или отсутствовать нулевой элемент.

ШКАЛЫ РАЗНОСТЕЙ (ИНТЕРВАЛОВ) - отличаются от шкал порядка тем, что для описываемых ими свойств имеют смысл не только соотношения эквивалентности и порядка, но и суммирования интервалов (разностей) между различными количественными проявлениями свойств. Характерный пример - шкала интервалов времени.

Интервалы времени (например, периоды работы, периоды учебы) можно складывать и вычитать, но складывать даты каких-либо событий бессмысленно.

Другой пример, шкала длин (расстояний) - пространственных интервалов определяется путем совмещения нуля линейки с одной точкой, а отсчет делается у другой точки. К этому типу шкал относятся и шкалы температур по Цельсию, Фаренгейту, Реомюру.

В этих шкалах допустимы линейные преобразования, в них применимы процедуры для отыскания математического ожидания, стандартного отклонения, коэффициента ассиметрии и смещенных моментов.

ШКАЛЫ ОТНОШЕНИЙ. К множеству количественных проявлений в этих шкалах применимы соотношения эквивалентности и порядка - операции вычитания и умножения, (шкалы отношений 1-го рода - пропорциональные шкалы), а во многих случаях и суммирования (шкалы отношений 2-го рода - аддитивные шкалы).

Примерами шкал отношений являются шкалы массы (2-го рода), термодинамическая температурная шкала (1-го рода).

Массы любых объектов можно суммировать, но суммировать температуры разных тел нет смысла, хотя можно судить о разности и, отношении их термодинамических температур. Шкалы отношений широко используются в физике и технике, в них допустимы все арифметические и статистические операции.

АБСОЛЮТНЫЕ ШКАЛЫ - обладают всеми признаками шкал отношений, но дополнительно в них существует естественное однозначное определение единицы измерений. Такие шкалы используются для измерений относительных величии (отношений одноименных величин: коэффициентов усиления, ослабления, КПД, коэффициентов отражений и поглощений, амплитудной модуляции и т.д.).

ЛОГАРИФМИЧЕСКИЕ ШКАЛЫ - логарифмическое преобразование шкал, часто применяемое на практике, приводит к изменению типа шкал. Практическое распространение получили логарифмические шкалы на основе применения систем десятичных и натуральных логарифмов, а также логарифмов с основанием два.

Логарифм есть число безразмерное, поэтому перед логарифмированием преобразуемая размерная величина в начале обращается в безразмерную путем ее деления на принятое по соглашению произвольное (опорное) значение той же величины, после чего выполняется операция логарифмирования.

В зависимости от типа шкалы, подвергнутой логарифмическому преобразованию, логарифмические шкалы могут быть двух видов. При логарифмическом преобразовании абсолютных шкал получаются абсолютные логарифмические шкалы, называемые иногда логарифмическими шкалами с плавающим нулем, т.к. в них не фиксируется опорное значение. Примерами таких шкал являются шкалы усиления (ослабления) сигнала в дБ. Для значений величин в абсолютных логарифмических шкалах допустимы операции сложения и вычитания.

БИОФИЗИЧЕСКИЕ ШКАЛЫ. В метрологической практике существует ряд шкал, которыми описываются реакции биологических объектов, прежде всего человека, на воздействующие на них физические факторы. К ним относятся шкалы световых и цветовых измерений, шкалы восприятия звуков, шкалы эквивалентных доз ионизирующих излучений и др. Будем называть такие шкалы биофизическими.

Биофизическая шкала - шкала измерений свойств физического фактора (стимула), модифицированная таким образом, чтобы по результатам измерений этих свойств можно было прогнозировать уровень или характер реакции биологического объекта на действие этого фактора.

Корреля́ция (корреляционная зависимость) — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин. 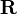Математической мерой корреляции двух случайных величин служит корреляционное отношение , либо коэффициент корреляции (или 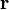). В случае, если изменение одной случайной величины не ведёт к закономерному изменению другой случайной величины, но приводит к изменению другой статистической характеристики данной случайной величины, то подобная связь не считается корреляционной, хотя и является статистической.

Корреляционным моментом (Ковариация) µ_xy случайных величин X и У называют математическое ожидание произведения отклонений этих величин:

µ_xy = M { [ X - M(X) ] [ Y - M(Y) ] }

Для нахождения корреляционного момента дискретных величин используют формулу:

,

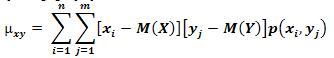а для непрерывных величин — формулу :

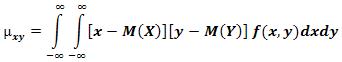
Корреляционный момент характеризует наличие (отсутствие) связи между величинами X и У. Ниже будет доказано, что корреляционный момент равен нулю, если X и У независимы; Если же корреляционный момент для случайных величин X и Y не равен нулю, то между ними имеется завимость.

Замечание 1. Приняв во внимание, что отклонения есть центрированные случайные величины, можно дать корреляционному моменту определение, как математическому ожиданию произведения двух центрированных случайных величин:

µ_xy= М [X_цY_ц].

Замечание 2. Не сложно доказать, что корреляционный момент можно записать в виде

µ_xy= М (ХY) – М(X) М(У).