Понятие о потоке жидкости.

ГИДРОСТАТИКА

4. Уравнение Эйлера.

Выделим в жидкости некоторый объем. Полная сила, действующая на выделенный объем жидкости, равна интегралу

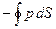(12)

от давления, взятому по поверхности рассматриваемого объема. Преобразуя его в интеграл по объему, имеем:

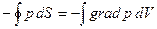(13)

Отсюда видно, что на каждый элемент объема dV жидкости действует со стороны окружающей его жидкости сила 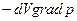. Другими словами, можно сказать, что на единицу объема жидкости действует сила -grad р.

Мы можем теперь написать уравнение движения элемента объема жидкости, приравняв силу -grad p произведению массы 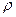единицы объема жидкости на ее ускорение :

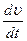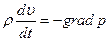. (14)

Стоящая здесь производная 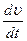определяет не изменение скорости жидкости в данной неподвижной точке пространства, а изменение скорости определенной передвигающейся в пространстве частицы жидкости. Эту производную надо выразить через величины, относящиеся к неподвижным в пространстве точкам. Для этого заметим, что изменение вскорости данной частицы жидкости в течение времени dt складывается из двух частей: из изменения скорости в данной точке пространства в течение времени dt и из разности скоростей (в один и тот же момент времени) в двух точках, разделенных расстоянием dr, пройденным рассматриваемой частицей жидкости в течение времени dt. Первая из этих частей равна

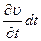(15)

где теперь производная 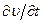берется при постоянных х, у, z, т.е. в заданной точке пространства. Вторая часть изменения скорости равна

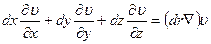(16)

Таким образом,

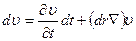(17)

или, разделив обе стороны равенства на dt,

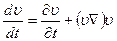. (18)

Подставляя полученное соотношение в (14), находим:

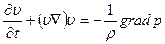. (19)

Это и есть искомое уравнение движения жидкости, установленное впервые Л. Эйлером в 1775 г. Оно называется уравнением Эйлера является одним из основных уравнений гидродинамики.

Если жидкость находится в поле тяжести, то на каждую единицу ее объема действует еще сила 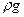, где g есть ускорение силы тяжести. Эта сила должна быть прибавлена к правой стороне уравнения (14), так что (19) приобретает вид

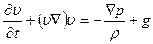. (20)

При выводе уравнений движения мы совершенно не учитывал процессов диссипации энергии, которые могут иметь место в текущей жидкости вследствие внутреннего трения (вязкости) в жидкости и теплообмена между различными ее участками. Поэтому все излагаемое здесь относится только к таким движениям жидкостей и газов, при которых несущественны процессы теплопроводности и вязкости; о таком движении говорят как о движении идеальной жидкости.

Отсутствие теплообмена между отдельными участками жидкости (а также, конечно, и между жидкостью и соприкасающимися с нею окружающими телами) означает, что движение происходит адиабатически, причем адиабатически в каждом из участков жидкости. Таким образом, движение идеальной жидкости следует рассматривать как адиабатическое.

При адиабатическом движении энтропия каждого участка жидкости остается постоянной при перемещении последнего в пространстве. Обозначая посредством 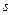энтропию, отнесенную к единице массы жидкости, мы можем выразить адиабатичность движения уравнением

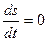, (21)

где полная производная по времени означает, как и в (14), изменение энтропии заданного перемещающегося участка жидкости. Эту производную можно написать в виде

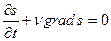. (22)

Это есть общее уравнение, выражающее собой адиабатичность движенияидеальной жидкости. С помощью 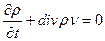его можно написать в виде «уравнения непрерывности» для энтропии

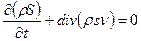. (23)

Произведение psv представляет собой «плотность потока энтропии».

Надо иметь в виду, что обычно уравнение адиабатичности принимает гораздо более простую форму. Если, как это обычно имеет место, в некоторый начальный момент времени энтропия одинакова во всех точках объема жидкости, то она останется везде одинаковой и неизменной со временем и при дальнейшем движении жидкости. В этих случаях можно, следовательно, писать уравнение адиабатичности просто в виде

s = const. (24)

что мы и будем обычно делать в дальнейшем. Такое движение называют изэнтропическим.

Изэнтропичностью движения можно воспользоваться для того, чтобы представить уравнение движения (19) в несколько ином виде. Для этого воспользуемся известным термодинамическим соотношением

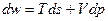, (25)

где w – тепловая функция единицы массы жидкости, 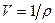– удельный объем, а Т – температура. Поскольку s = const, мы имеем просто

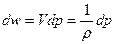, (26)

и поэтому 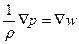. Уравнение (19) можно, следовательно, написать в виде

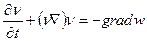. (27)

Полезно заметить еще одну форму уравнения Эйлера, в котором оно содержит скорость. Воспользовавшись известной формулой векторного анализа

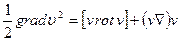, (28)

можно написать (29) в виде

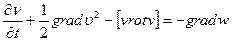. (29)

Если применить к обеим строкам этого уравнения операцию rot, то мы получим уравнение

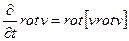, (30)

содержащее только скорость.

К уравнениям движения надо добавить граничные условия, которые должны выполняться на ограничивающих жидкость стенках. Для идеальной жидкости это условие должно выражать собой просто тот факт, что жидкость не может проникнуть за твердую поверхность. Это значит, что на неподвижных стенках должна обращаться в нуль нормальная к поверхности стенки компонента скорости жидкости:

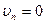(31)

(в общем же случае движущейся поверхности 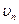должно быть равно соответствующей компоненте скорости поверхности).

На границе между двумя несмешивающимися жидкостями должны выполняться условие равенства давлений и условие равенства нормальных к поверхности раздела компонент скорости обеих жидкостей (причем каждая из этих скоростей равна скорости нормального перемещения самой поверхности раздела).

Как уже было указано, состояние движущейся жидкости определяется пятью величинами: тремя компонентами скорости 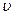и, например, давлением р и плотностью 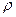. Соответственно этому полная система гидродинамических уравнений должна содержать пять уравнений. Для идеальной жидкости этими уравнениями являются уравнения Эйлера, уравнение непрерывности и уравнение, выражающее адиабатичность движения.

1. Основная формула гидростатики.

Закон Паскаля. Понятие о напоре

Рассмотрим абсолютный покой несжимаемой жидкости в поле силы тяжести.

Уравнение Эйлера (20) принимает вид

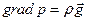. (32)

Это уравнение описывает механическое равновесие жидкости. Если внешние силы вообще отсутствуют, то уравнение равновесия гласит просто 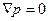, т.е. р = const – давление одинаково во всех точках жидкости.

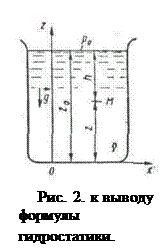
Уравнение (32) непосредственно интегрируется, если плотность жидкости можно считать постоянной вдоль всего объекта, т.е. если не происходит заметного сжатия жидкости под действием внешнего поля. Выберем оси координат, как показано на рис. 2. Поскольку из массовых сил действует только сила тяжести, то

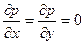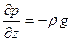; . (33)

Таким образом, искомая функция р зависит только от одной переменной z; интегрирование последнего равенства дает

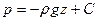, (34)

где С – произвольная постоянная.

Эта формула выражает гидростатический закон распределения давления, состоящий в том, что в тяжелой (подверженной действию силы тяжести) несжимаемой жидкости давление линейно зависит от вертикальной координаты.

Чтобы найти постоянную в уравнении (34), надо использовать какое-нибудь граничное условие. Пусть, например, жидкость покоится в резервуаре (см. рис.2) причем на ее свободной поверхности давление равно р₀. Будем это давление называть внешним.

Для точек свободной поверхности можем записать

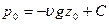. (35)

Вычитая это отношение из уравнения (34), находим

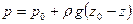(36)

или, обозначив через 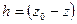заглубление точки М под свободную поверхность, получим основную формулу гидростатики

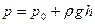, (37)

где величина 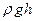называется весовым давлением.

Из этой формулы ясно, что всякое изменение внешнего давления 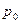вызывает изменение давления во всех точках покоящейся жидкости на ту же величину. Этот результат известен как закон Паскаля.

Если жидкость находится в ненапряженном состоянии, т.е. в ней отсутствуют напряжения сжатия, то 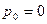. Значения 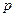, отсчитанные от нуля, называют иногда абсолютным давлением.

В технике весьма часто представляет интерес избыток давления р над атмосферным 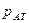, который называется избыточным или манометрическим давлением. По определению

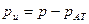. (38)

Для произвольной точки М, заглубленной на высоту h под свободную поверхность, избыточное давление равно

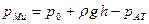; (39)

отсюда видно, что избыточное давление совпадает с весовым, если давление на свободной поверхности равно атмосферному ( ).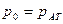

Если все члены формулы (37) разделить на величину 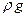, то они приобретут линейную размерность:

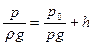. (40)

Отсюда следует, что каждому давлению р можно поставить в соответствие линейную величину 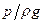, которая представляет собой величину столба жидкости, создающего в своем основании данное давление. Это наглядно иллюстрируется схемой, показанной на рис.3. Если на свободной поверхности в резервуаре давление 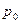, а из запаянной сверху трубки А удален воздух, то под действием давления 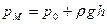жидкость в трубке поднимется над точкой М на некоторую высоту 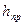, называемую приведенной высотой. Принимая приближенно, что на свободной поверхности в трубке давление равно нулю, согласно (37) можно записать 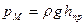. Следовательно, приведенная высота есть высота столба жидкости, на свободной поверхности которого давление равно нулю, а в основании – данному давлению жидкости.

Для трубки П, открытой в атмосферу и называемой пьезометром, получим

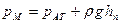, (41)

откуда

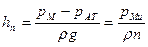; (42)

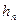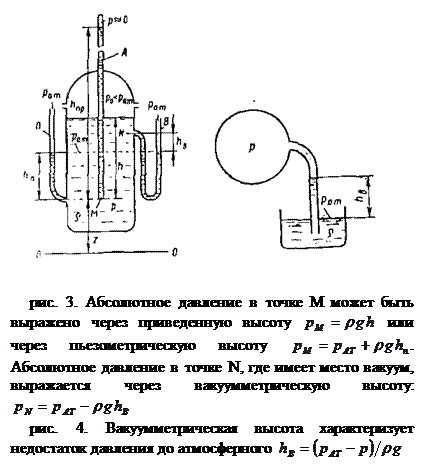
величину называют пьезометрической высотой.

Если давление в точках какого-либо объема жидкости меньше атмосферного ( 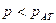), то такое состояние называется вакуумом. Для его характеристики вводится понятие вакуумметрического давления ( 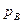), под которым подразумевается недостаток данного давления до атмосферного

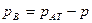. (43)

Соответствующая высота называется вакуумметрической:

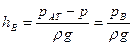. (44)

На рис. 3 и 4 показаны вакуумметрические высоты для случаев вакуума в капельной жидкости и газе. Давление измеряется в единицах силы, отнесенных к единице площади. В системе СИ единицей давления служит Н/м² = Па (паскаль), а в технической системе – кгс/см² = ат (техническая атмосфера). Наряду с этими, как следует из (42) и (44), давление можно, измерять в единицах длины столба данной жидкости.

Общей формулой перевода единиц давления в линейные единицы является

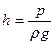. (45)

При выражении давления высотой столба жидкости чаще всею применяют метры водяного столба, миллиметры ртутного столба и миллиметры спиртового столба.

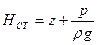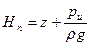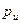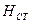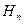Гидростатический закон распределения давления, выраженный формулой (34), справедлив, очевидно, для любого положения координатной плоскости хОу. Эту плоскость называют плоскостью сравнения, а величину – гидростатическим напором. Величину , где – избыточноедавление, называют пьезометрическим напором. Из формулы (34) следует, что напоры и постоянны для всех точек данной массы покоящейся жидкости.

2. Силы давления жидкости на твердые поверхности

В общем случае воздействие жидкости на твердую поверхность S сводится к сумме элементарных сил 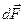, действующих на малых площадках dS, составляющих эту поверхность (рис. 5).

Если 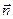– единичный вектор нормали к поверхности S, внешней к объему жидкости, а 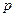– давление на площадке dS, то сила .

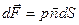Суммируя систему сил 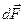, получаем выражение для главного вектора

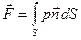, (46)

называемого силой давления жидкости на поверхность S, и выражение для главного момента

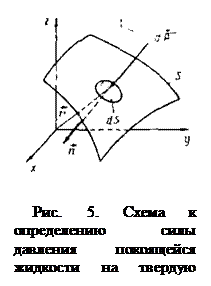
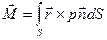, (47)

где 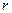– радиус-вектор площадки 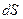относительно центра приведения системы сил.

Рассмотрим несколько частных случаев.

2.1. Равномерное давление на плоскую стенку (р=const., п=const).

В этом случае суммируемые векторы 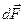составляют систему параллельных и одинаково направленных сил. Такая система всегда может быть сведена только к силе давления 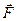. При р = const и n = const из выражения (46) получаем

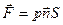. (48)

Линия действия силы 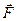проходит через центр тяжести площади S.

Равномерное давление может создаваться покоящимся газом, так как благодаря малой его плотности можно пренебречь действием массовых сил и считать давление одинаковым во всех точках газа.

Равномерное давление может создаваться и капельной жидкостью, например, при ее воздействии на горизонтальные площадки, в случае абсолютного покоя или движения сосуда с ускорением вверх или вниз.

Величина силы 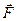при равномерном распределении давления не зависит от ориентации плоской стенки S в пространстве и вычисляется по формуле .

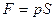Например, для схемы на рис. 6 давление на дне 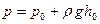, а сила 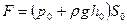. Заметим, что сила давления на дно не зависит от формы сосуда (гидростатический парадокс).

2.2. Сила равномерного давления на криволинейную стенку ( , )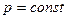

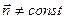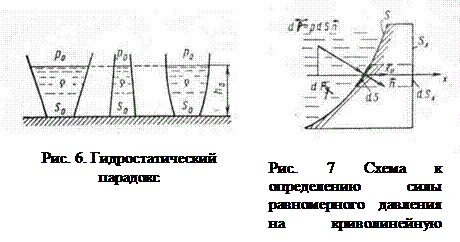
В этом случае элементарные силы 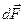имеют разные направления. Главный вектор 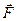системы вычисляется через свои проекции. Чтобы найти его проекцию 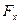на ось х , проектируем на эту ось векторы 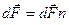(рис.7).

,

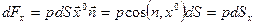где 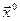– единичный вектор оси x; 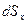– проекция площадки dS на плоскость, нормальную оси х. Искомая величина 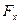при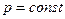

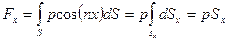. (49)

Линия действия силы 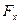проходит через центр тяжести площади проекции 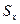. Таким образом, величина проекции на направлении оси x силы равномерного давления р на криволинейную поверхность S равна произведению давления и площади проекции S_x этой криволинейной поверхности на плоскость. нормальной оси х. Если такие проекции на три взаимно ортогональные оси пересекаются в одной точке, то система сил 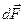может быть сведена только к силе давления, величина которой

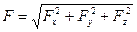, (50)

а направление определяется направляющими косинусами

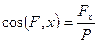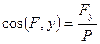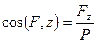; ; . (51)

Если составляющие не пересекаются в одной точке, система сводится к силе и моменту.

2.3. Сила неравномерного давления на плоскую стенку ( , ).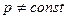

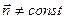Систему элементарных сил 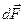, одинаковых по направлению, но различных по величине, можно свести в данном случае к одной силе давления

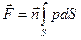, (52)

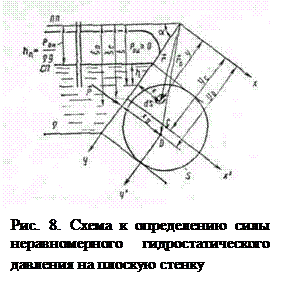где S – площадь стенки.

Величина этой силы

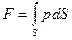(53)

зависит от закона распределения давления Р по площади S. При воздействии на S капельной жидкости эти законы могут быть различными. Их конкретный вид зависит от ориентации площадки и действующих на жидкость массовых сил при абсолютном и относительном покое.

Вычислим силу 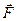для плоской стенки, наклоненной к горизонту под углом a и подверженной воздействию тяжелой жидкости, находящейся в состоянии абсолютного покоя (рис. 8).

Определим результирующую силу избыточных давлений 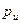, которые создаются внешним избыточным 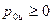и весовым 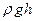давлениями. Заменим внешнее давление 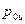воздействием эквивалентного слоя жидкости, толщина, которого 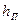определяется высотой поднятия жидкости в пьезометре 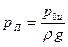. Таким образом, внешнее давление из рассмотрения исключается, и свободная поверхность СП заменяется пьезометрической плоскостью ПП. Продолжим плоскость стенки до пересечения с пьезометрической плоскостью. Вдоль линии их пересечения направим ось х, а ось у расположим в плоскости стенки. Затем для наглядности повернем плоскость стенки на 90° вокруг оси у и совместим стенку с плоскостью чертежа.

Величину силы вычислим по формуле (53):

.

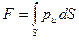В рассматриваемом случае (см. рис. 8) давление

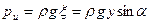, (54)

что при подстановке в формулу (53) дает

.

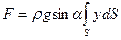Интеграл 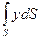представляет собой статический момент площади S относительно оси Ох, равный, как известно, произведению S на координату 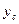ее центра тяжести.

Поэтому

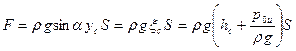. (55)

Формула (55) может быть записана в двух видах

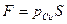, (56)

где 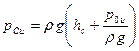– избыточное давление в центре тяжести площадиS, или

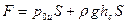. (57)

Согласно (56) величина силы избыточного давления покоящейся жидкости на плоскую стенку равна произведению площади стенки на избыточное давление в ее центре тяжести.

Вектор силы 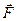направлен по нормали к стенке S:

,

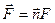а линия действия этой силы пересекает стенку в некоторой точке D, называемой центром давления. Для отыскания координат этой точки ( 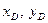) используем теорему о равенстве момента равнодействующей и суммы моментов составляющих, которая в данном случае выражается уравнением

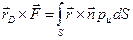, (58)

где 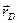и 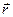– радиус-векторы соответственно центра давления D и произвольной точки (ху) площади S.

По правилам составления проекций векторного произведения находим

; .

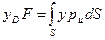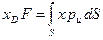Учитывая выражения (54) и (55), получим

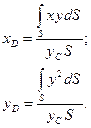(59)

Более удобные выражения для 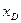и 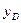получим, если воспользуемся теоремой о соотношении между моментами второй степени, взятыми относительно параллельных осей

; ,

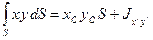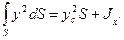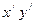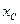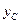где – оси координат, проходящие через центр тяжести С площадки S параллельно осям х и у; и – координаты центра тяжести С в системе xу; 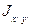– центробежный момент площади S относительно осей х и у ; 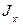– момент инерции площади S относительно оси х (см. рис. 8). Окончательно,

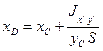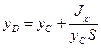; . (60)

Вторая из формул (60) показывает, что центр давления расположен ниже центра тяжести на величину .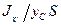

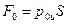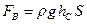Возвращаясь к формуле (57), заметим, что силу давления в рассматриваемом случае можно получить, складывая независимо вычисленные две силы: и , где 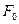– сила внешнего избыточного давления, 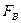– сила весового давления. При таком способе определения силы 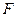следует помнить, что линии действия сил 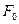и 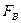не совпадают, и центр давления D определяется линией действия суммарной силы .

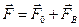2.4. Неравномерное давление на криволинейную твердую поверхность ( 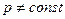, 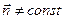) может быть создано тяжелой жидкостью при абсолютном или относительном покое. Элементарные силы 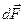составляют в этом случае самую общую систему, которая должна сводиться к силе давления 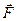(46) и моменту 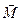(47). Однако существуют частные случаи,, когда система сводится к одной силе давления 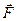, например, если линии действия элементарных сил 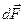пересекаются в одной точке (сферическая стенка).

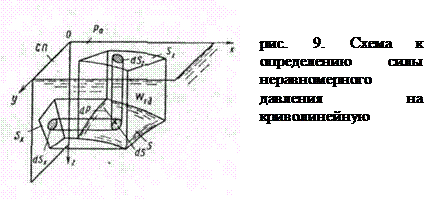
Рассмотрим криволинейную поверхность S, находящуюся под воздействием внешнего избыточного давления 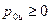и весового давления 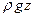(рис.9). Как было показано в предыдущем пункте, задачу отыскания силы давления можно расчленить, определяя раздельно силы весового и внешнего давлений. Эту же задачу можно свести к задаче об определении только весового давления, заменив внешнее давление действием эквивалентного слоя жидкости.

Силу весового давления 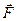определим по ее проекциям. Горизонтальная проекция

,

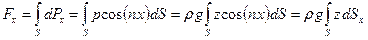где 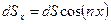– проекция площадки dS на вертикальную плоскость, нормальную к оси х. Последний интеграл представляет собой статический момент площади 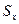относительно оси y. Следовательно,

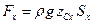, (61)

где 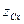– координата центра тяжести площади .

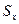Аналогично получим

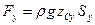, (62)

где 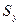– площадь проекции криволинейной поверхности на плоскость, нормальную оси y.

Таким образом, чтобы вычислить горизонтальную проекцию 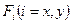силы весового давления на криволинейную поверхность, следует площадь проекции 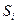этой поверхности на плоскость, нормальную к рассматриваемой горизонтальной оси, умножить на давление в центре тяжести площади .

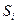Проекция силы весового давления на вертикальную ось определится соотношением

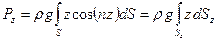, (63)

где 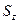– проекция на плоскость х0у поверхности S.

Последний интеграл представляет собой объем тела 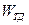, ограниченного поверхностью S, цилиндрической боковой поверхностью 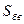с вертикальными образующими и проекцией 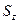криволинейной поверхности S на свободную поверхность жидкости. Это тело называется телом давления, а величина 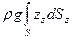есть вес жидкости в его объеме.

Таким образом, вертикальная проекция силы весового давления на криволинейную поверхность равна весу жидкости в объеме тела давления.

Величина 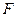силы 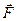определится формулой

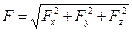, (64)

а направление линии ее действия – направляющими косинусами

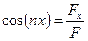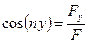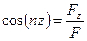; ; . (65)

Есл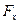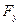и , и 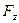пересекаются в одной точке, то система сводится к силе давления, проходящей через эту точку.

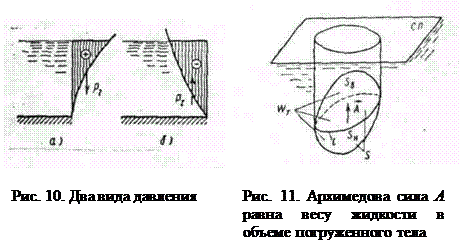
Возможны два случая расположения криволинейной поверхности (рис. 10 а и б) под уровнем жидкости. В первом случае жидкость расположена над твердой поверхностью; тело давления заполнено жидкостью и считается положительным, а вертикальная составляющая силы направлена вниз. Во втором случае тело давления не заполнено жидкостью и считается отрицательным; вертикальная сила давления направлена вверх.

Если криволинейная поверхность S замкнута и полностью погружена под уровень абсолютно покоящейся жидкости (рис. 11), то воздействие жидкости сводится к одной вертикальной силе. Действительно, для любой горизонтальной оси существуют две противоположно направленные и равные по величине силы, действующие на тело; поэтому результирующая горизонтальных сил равна нулю. Чтобы найти вертикальную силу, проектируем S на свободную поверхность жидкости. Проектирующие вертикали отметят на поверхности тела замкнутую линию l, которая делит поверхность на две част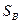и и 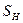. Для верхней части 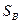тело давления положительно и соответствующая ему сила направлена вертикально вниз, а для нижней 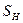– тело давления отрицательно и сила направлена вверх. Обозначив объемы этих тел давления соответственно через 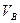и 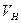, найдем величину результирующей вертикальной силы А:

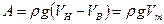, (66)

где 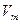– объем тела.

Таким образом, сила давления покоящейся жидкости на погруженное в нее тело направлена вертикально вверх и равна весу жидкости в объеме тела. Этот результат составляет содержание закона Архимеда: сила А называется архимедовой или гидростатической подъемной силой. Если G – вес тела, то его плавучесть определяется соотношением сил А и G. При 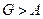тело тонет, при 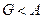– всплывает, при G = А – плавает в состоянии безразличного равновесия. Следует иметь в виду, что линии действия сил G и А могут не совпадать, так как линия действия веса G проходит через центр тяжести тела, а линия действия архимедовой силы А – через центр его объема. При неравномерном распределении плотности тела может появиться момент, способствующий опрокидыванию тела.

В заключение отметим, что сила давления жидкости по криволинейной поверхности в случаях относительного покоя может быть определена общим способом суммирования элементарных сил давления, применительно к заданной форме поверхности и условиям относительного покоя.

ГИДРОДИНАМИКА

Основные понятия гидродинамики

Основные элементы движения жидкости. Причинами движения жидкости являются действующие на нее силы: объемные или массовые силы (сила тяжести, инерционные силы) и поверхностные силы (давление, трение). В отличие от гидростатики, где основной величиной, характеризующей состояние покоя жидкости, является гидростатическое давление, которое определяется только положением точки в пространстве, т.е. 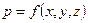,в гидродинамике основными элементами, характеризующими движение жидкости, будут два: гидродинамическое давление и скорость движения (течения) жидкости.

Гидродинамическое давление р – это внутреннее давление. развивающееся при движении жидкости. Скорость движения жидкости в данной точке и – это скорость перемещения находящейся в данной точке частицы жидкости, определяемая длиной пути l, пройденного этой частицей за единицу времени t.

В общем случае основные элементы движения жидкости р и и для данной точки зависят от ее положения в пространстве (координат точки) и могут изменяться во времени. Аналитически это положение гидродинамики записывается так:

,

.

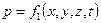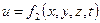Задачей гидродинамики и является определение основных элементов движения жидкости р и u, установление взаимосвязи между ними и законов изменения их при различных случаях движения жидкости.

Траектория частицы.Если в массе движущейся жидкости взять какую-либо частицу жидкости и проследить ее путь за какой-то промежуток времени 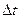(конечный, достаточно большой), то можно получить некоторую линию, выражающую геометрическое место этой точки в пространстве за время .

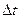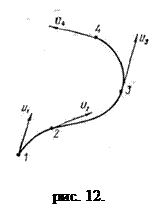Линия тока. Если в массе движущейся жидкости в данный момент времени t взять какую-либо точку 1(рис. 12), то можно в этой точке построить вектор скорости и₁, выражающий величину и направление скорости движения частицы жидкости в данной точке 1в этот момент времени.

В тот же момент времени t можно взять и другие точки в движущейся жидкости, например, точки 2, 3, 4,. ..... в которых также можно построить векторы скоростей u₂, u₃, и₄,… выражающие скорость движения других частиц жидкости в тот же момент.

Можно выбрать точки 1, 2, 3, 4. . . и провести через них плавную кривую, к которой векторы скоростей будут всюду касательны. Эта линия и называется линией тока.

Таким образом, линией тока называется линия, проведенная через ряд точек в движущейся жидкости так, что в данный момент времени векторы скорости частиц жидкости, находящихся в этих точках, направлены по касательной к этой линии. В отличие от траектории, которая показывает путь движения одной частицы жидкости за определенный промежуток времени 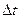, линия тока соединяет разные частицы и дает некоторую мгновенную характеристику движущейся жидкости в момент времени t. Через заданную точку в данный момент времени можно провести только одну линию тока.

Если в данных точках движущейся жидкости величина и направление скорости и гидродинамическое давление с течением времени не изменяются (такое движение называется установившимся), то и линия тока, и траектория частицы, оказавшейся на ней, совпадают и со временем не изменяются. В этом случае траектории частиц являются и линиями тока.

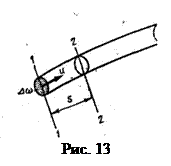Элементарная струйка. Если в движущейся жидкости выделить весьма малую элементарную площадку 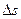, перпендикулярную направлению течения, и по контуру ее провести линии тока, то полученная поверхность называется трубкой тока, а совокупность линий тока, проходящих сплошь через площадку 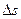, образует так называемую элементарную струйку (рис. 13).

Элементарная струйка характеризует состояние движения жидкости в данный момент времени t. При установившемся движении элементарная струйка имеет следующие свойства:

1. форма и положение элементарной струйки с течением времени остаются неизменными, так как не изменяются линии тока;

2. приток жидкости в элементарную струйку и отток из нее через боковую поверхность невозможен, так как по контуру элементарной струйки скорости направлены по касательной;

3. скорость и гидродинамическое давление во всех точках поперечного лечения элементарной струйки можно считать одинаковым ввиду малости площади .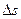

Поток. Совокупность элементарных струек движущейся жидкости, проходящих через площадку достаточно больших размеров, называется потоком жидкости. Поток ограничен твердыми поверхностями, по которым происходит движение жидкости (труба), и атмосферой (река, лоток, канал и т.п.).

Понятие о потоке жидкости.

Гидравлические элементы потока. Живым сечением называется поверхность в пределах потока, проведенная перпендикулярно к линиям тока (элементарным струйкам). В общем случае эта поверхность криволинейная (на рис. 14 поверхность ABC). Однако в большинстве случаев практической гидравлики поток жидкости можно представить параллельно-струйным или с очень малым углом расхождения струек, а за живое сечение принять плоское поперечное сечение потока (на рис. 14 плоскость АС). Площадь живого сечения обозначается 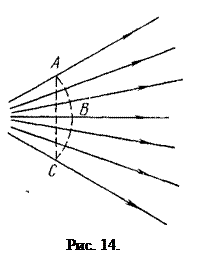буквой s.

Смоченным периметром называется длина части периметра живого сечения, в пределах которой поток соприкасается с твердыми внешними стенками. Смоченный периметр обозначают буквой П.

Гидравлическим радиусом называется отношение площади живого сечения к смоченному периметру:

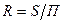. (67)

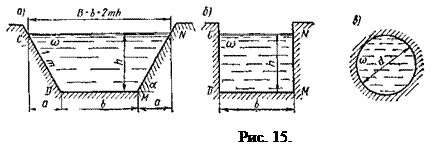
На рис. 15 приведены примеры поперечных сечений потока: а) трапецеидальное; б) прямоугольное; в) круговое.

Для кругового сечения, заполненного жидкостью полностью (рис. 15, в): ; ; .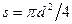

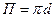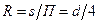Расход жидкости и средняя скорость. Расходом жидкости называется количество жидкости, проходящей через данное живое сечение потока в единицу времени.

Расход потока жидкости обозначают Q, а элементарной струйки – 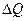. Единицами измерения расхода являются: м³/сек, м³/ч или л/сек, л/ч и др.

Рассмотрим элементарную струйку (рис. 13) с поперечным сечением 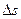и постоянной скоростью движения частицы жидкости и. Через промежуток времени t частицы переместятся из сечения 1-1 в сечение 2-2 на расстояние l. При этом через сечение 1-1 пройдет элементарный объем жидкости 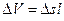. Разделив обе части уравнения на t, получим

,

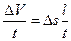но 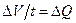–расход элементарной струйки (объем, прошедший через элемент живого сечения 1-1 в единицу времени); 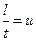–скорость движения частиц жидкости (путь, пройденный частицами жидкости за единицу времени).

Отсюда

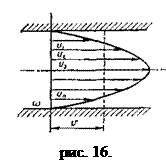
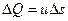, (67a)

т. е. расход элементарной струйки равен площади ее поперечного сечения, умноженной на скорость в этом сечении. Поток жидкости в данном живом сечении представляет совокупность (сумму) большого числа элементарных струек, заполняющих сплошь площадь живого сечения, поэтому для определения расхода потока через живое сечение s необходимо взять сумму расходов 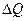элементарных струек, т.е.

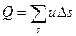. (67б)

В общем случае, чтобы воспользоваться формулой (67б) для определения расхода потока, надо знать закон распределения скоростей по живому сечению, который очень сложен или вообще неизвестен. Поэтому для практических расчетов вводится понятие средней скорости потока.

На рис. 16 представлен график (эпюра) распределения действительных скоростей в точках живого сечения потока, из которого видно, что скорости по сечению распределяются неравномерно. При действительных скоростях через живое сечение проходит определенный расход Q. Можно найти некоторую постоянную для всех точек сечения фиктивную скорость, при которой через данное сечение проходил бы тот же самый расход, что и при действительных скоростях движения жидкости. Эта скорость v будет средней из действительных скоростей. Подставляя в формулу (67б) скорость v получим 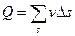, но 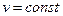, ,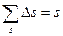поэтому

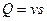, (68)

т. е. расход жидкости в данном сечении потока равен произведению средней скорости движения жидкости, умноженной на площадь живого сечения.

Итак, средней скоростью потока в данном сечении v называется такая одинаковая для всех точек живого сечения скорость движения жидкости, при которой через это живое сечение проходит тот же расход Q, что и при действительных скоростях движения жидкости и.

Из формулы (68) можно написать

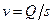, (68^/)

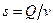. (68^//)

Формулы (68), (68') и (68") используются при решении основных гидравлических задач, связанных с потоком жидкости. Их следует четко знать и запомнить.

Виды движения жидкости

Установившимся стационарным движением жидкости называется такое движение, при котором в каждой данной точке основные элементы движения жидкости – скорость движения и и гидродинамическое давление р не изменяются с течением времени, т.е. зависят только от координат точки. Аналитически это условие запишется так:

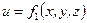и .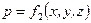

Неустановившимся (нестационарным) движением жидкости называется такое движение, при котором в каждой данной точке основные элементы движения жидкости – скорость движения и и гидродинамическое давление р – постоянно изменяются, т.е. зависят не только от положения точки в пространстве, но и от времени 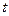. Аналитически это условие запишется так:

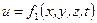и .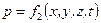

Примером установившегося движения может быть: движение жидкости в канале, в реке при неизменных глубинах, истечение жидкости из резервуара при постоянном уровне жидкости в нем и др. Неустановившееся движение – это движение жидкости в канале или реке при переменном уровне или при опорожнении резервуара, когда уровень жидкости в нем непрерывно изменяется.

В дальнейшем будет изучаться главным образом установившееся движение жидкости и в отдельных случаях будут разбираться примеры неустановившегося движения.

Установившееся движение в свою очередь подразделяется на равномерное и неравномерное.

Равномерным называется такое установившееся движение, при котором живые сечения вдоль потока не изменяются: в этом случае 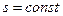; средние скорости по длине потока также не изменяются, т.е. 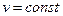. Примером равномерного движения является: движение жидкости в цилиндрической трубе, в канале постоянного сечения при одинаковых глубинах.

Установившееся движение называется неравномерным, когда распределение скоростей в различных поперечных сечениях неодинаково; при этом средняя скорость и площадь поперечного сечения потока могут быть и достоянными вдоль потока. Примером неравномерного движения может быть движение жидкости в конической трубе или в речном русле переменной ширины.

Напорным называется движение жидкости, при котором поток полностью заключен в твердые стенки и не имеет свободной поверхности. Напорное движение происходит вследствие разности давлений и под действием силы тяжести. Примером напорного движения является движение жидкости в замкнутых трубопроводах (например, в водопроводных трубах).

Безнапорным называется движение жидкости, при котором поток имеет свободную поверхность. Примером безнапорного движения может быть: движение жидкости в реках, каналах, канализационных и дренажных трубах. Безнапорное движение происходит под действием силы тяжести и за счет начальной скорости. Обычно на поверхности безнапорного потока давление атмосферное.

Следует отметить еще один вид движения: свободную струю. Свободной струей называется поток, не ограниченный твердыми стенками. Примером может служить движение жидкости из пожарного брандспойта, гидромонитора, водопроводного крана, из отверстия резервуара и т. п. В этом случае движение жидкости происходит по инерции (т. е. за счет начальной скорости) и под действием силы тяжести.

Для упрощения выводов, связанных с изучением потока жидкости, вводится понятие о плавно изменяющемся движении жидкости.

Плавно изменяющимся называется такое движение жидкости, при котором кривизна струек незначительна (равна нулю или близка к нулю) и угол расхождения между струйками весьма мал (равен нулю или близок к нулю), т. е. практически поток жидкости мало отличается от параллельноструйного. Это предположение вполне оправдывается при изучении многих случаев движения жидкости в каналах, трубах и других сооружениях.

Отметим следующие свойства потока при плавно изменяющемся движении:

1. поперечные сечения потока плоские, нормальные к оси потока;

2. распределение гидродинамических давлений по сечению потока подчиняется закону гидростатики, т.е. гидродинамические давления по высоте сечения распределяются по закону прямой. Это свойство легко можно доказать, если внутри потока выделить частицу жидкости и спроектировать все действующие на нее силы на плоскость живого сечения. Вследствие того, что скорости и ускорения в этом случае будут перпендикулярны сечению, силы инерции в уравнение не войдут; поэтому уравнение равновесия и закон распределения давления в плоскости живого сечения не будет отличаться от такового для жидкости, находящейся в покое;

3. удельная потенциальная энергия (т. е. потенциальная энергия единицы веса жидкости) по отношению к некоторой плоскости сравнения для всех точек данного сечения потока жидкости есть величина постоянная.