Основы расчета плужных снегоочистителей

Расчеты плужных снегоочистителей могут преследовать цели: определить зону отбрасывания снега около пути, найти сопротивление движению при работе, оценить устойчивость против схода с рельсов и поперечного опрокидывания при работе и транспортировании, произвести расчет нагрузок на плуги и механизмы привода для определения их основных параметров и др.

12.2.1. Расчет ширины зоны отброса снега при работе снегоочистителя

Снежный покров на пути зависит от снежных осадков и снежных заносов [25]. Толщина покрова за один снегопад обычно не превышает 0,2-0,25 м, вместе с тем, при снежных заносах образуется плотный покров с толщиной до нескольких метров. Толщина заноса зависит от поперечного профиля земляного полотна и количества снега, приносимого к пути при наиболее снежной зиме. Путь, расположенные на насыпи, высота которой больше толщины снежного покрова, как правило, не подвержен снежным заносам. Это, как правило, насыпи с высотой более 0,7 м. Выемки глубиной более 0,4 м подвержены сильной заносимости. По степени заносимости различают участки пути: особо сильно заносимые, сильно заносимые, средне заносимые и слабо заносимые. Степень заносимости определяется объемами снега в м³, перемещаемого к пути в течение зимы, приходящегося на 1 пог.м пути (м³/пог. м). Например, к сильно заносимым относятся участки, у которых за зиму перенос снега составляет до 600 м³/пог. м.

Помимо толщины снежного покрова, на режим работы снегоочистителя оказывает влияние плотность снежного покрова. Выпавший снег образует слой с плотностью, не превышающей r = 150-200 кг/м³. При образовании заноса снег спрессовывается и достигает плотности, превышающей r = 600 кг/м³.

Распределение отброшенного при очистке снега вдоль пути, помимо толщины покрова и плотности, зависит также от формы рабочей поверхности отвала (рис. 12.8), скорости движения снегоочистителя V_м, м/с и угла наклона отвала a, рад к направлению движения (угла атаки). Современные плужные снегоочистители оснащаются плоскими отвалами (а), отвалами цилиндрической (б) и конической (в) формы. Отвалы, имеющие криволинейную форму рабочей поверхности, позволяют подрезать и отбрасывать снег на значительное расстояние от оси пути (рис. 12.9, б) при скорости снегоочистителя, превышающей 25-30 км/ч (7-8 м/с). Снег откидывается в полосу отвода с рассеянием по большой площади, не образуя вдоль пути вала. При меньшей скорости снег не поднимается до верхней кромки отвала, поэтому перед отвалом образуется призма волочения (рис. 12.9, а), а после сдвига снега с отвала рядом с путем остается вал снега. При накапливании значительного объема снега около пути требуется использовать, например, струг-снегоочиститель, чтобы земляным устройством отодвинуть вал.

Рассмотрим процесс отбрасывания снега отвалом [25] с рабочей поверхностью конической формы. Отвал цилиндрической формы тогда можно рассматривать как частный случай. При работе происходит движение снега по отвалу, которое рассматривается как относительное движение (система отсчета связана с отвалом). При подрезании слоя снега величина относительной скорости принимается равной величине скорости машины: V_о = V_м. Отвал рассматривается как клин (рис. 12.8, г), поэтому происходит подъем слоя снега по его рабочей поверхности со скоростью V_оsina и движение вдоль отвала со скоростью V_оcosa. Снег в заносе спрессован, поэтому пренебрежем также дополнительным прессованием снега, считая, что нижние слои снега на отвале подпирают верхние, поэтому не происходит замедление движения снега по отвалу. Коэффициент трения плотного снега по стальной поверхности отвала составляет f = 0,03-0,04, поэтому в модели, не требующей повышенной точности, трением можно пренебречь.

Рассмотрим движение подъема по отвалу частицы снега массой m, кг. В верхней точке 2 отвала (рис. 12.10, а) на частицу действует сила веса mg, Н, которую можно разложить на составляющие: 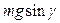, направленную по касательной к поверхности отвала, и 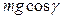, нормальную к указанной поверхности. Кроме того, на частицу действует центробежная сила 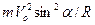, Н (R – радиус кривизны поверхности в рассматриваемом сечении, м), и реакция отвала N, Н. Спроектировав указанные силы на направление a – a, получим уравнение равновесия:

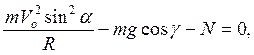(12.1)

где g – ускорение свободного падения, g = 9,8 м/с²; g – угол наклона касательной к горизонту в верхней точке отвала, рад.

Используя это выражение, с учетом того, что V_о = V_м, можно определить критическую для рассматриваемого поперечного сечения скорость движения снегоочистителя, при которой частица будет достигать верхней кромки отвала, м/с:

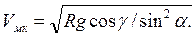(12.2)

При достижении критической скорости движения реакция отвала N = 0. Если скорость движения снегоочистителя меньше критической скорости для данного сечения, то частица сваливается с отвала, а перед отвалом может образовываться призма волочения. Если рассматривается крайнее сечение отвала, то расчет ведется по максимальному радиусу R_max, м. При превышении критической скорости для этого сечения отбрасывание слоя снега без образования призмы волочения гарантировано.

Вместе с подъемом частицы по отвалу происходит ее относ вдоль отвала (рис. 12.10, б). Частица начинает движение в сечении отвала с начальным радиусом R_н, м, а вылетает с отвала в сечении с радиусом R_в, м, смещаясь вдоль отвала на расстояние s, м. Определение этого относа позволяет оценить общую картину движения снега по отвалу. Очевидно, что 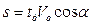, где t_д – время движения частицы по отвалу, с. Если рассматривать подъем частицы в проекции на сечение с радиусом R_в, м, то время подъема частицы будет определяться длиной дуги L_о, м (рис. 12.10, в) и скоростью подъема. После анализа кинематических соотношений, относ частицы:

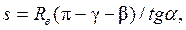(12.3)

где b – угол резания снега нижней кромкой отвала, рад.

В рассмотренной расчетной модели принято, что подъем частицы начинается от режущей кромки отвала. Для учета толщины срезаемого слоя h_c принимаем, что расчетная частица поднимается с середины слоя по его толщине (фиктивная «режущая кромка» поднята на высоту h_с/2 относительно нижней кромки отвала). Тогда фиктивный угол резания, который необходимо подставить в формулу (12.3), рад:

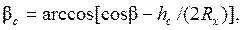(12.4)

Путь, проходимый слоем снега до верхней кромки отвала уменьшается, уменьшается также относ снега и дальность его отбрасывания. Хорошо отбрасывается слой плотного снега, толщина которого не превышает 0,4-0,5 м.

Выражение (12.3) позволяет относительно анализируемой точки вылета частицы определять точку начала подъема этой частицы. Значение радиуса R_x, м, для сечения на расстоянии x, м можно определять по интерполяционной формуле:

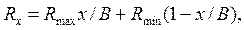(12.5)

где R_max, R_min – радиусы максимального и минимального сечений рабочей поверхности отвала, м; B – ширина отвала по режущей кромке, м.

Дальность отброса снега от оси пути зависит от величины относительной скорости движения по отвалу и углов наклона вектора указанной скорости к горизонту и к направлению движения снегоочистителя. Кроме того, снег имеет переносную скорость V_м вместе с движением снегоочистителя. Эта скорость определяет отброс частиц по направлению движения, который с практической точки зрения менее интересен. Рассмотрим относительное движение частицы снега, вылетевшей с верхней кромки отвала. Для упрощения рассуждений считаем, что верхняя кромка отвала параллельна нижней кромке, а частица вылетела под углом g к горизонту и под углом a к направлению движения снегоочистителя. Иначе говоря, плоскость полета частицы (рис. 12.10, г) расположена в плане, приблизительно, под углом a к продольной оси пути. Частица вылетает с верхней кромки отвала, поэтому имеет начальную высоту h_о = R(cosb + cosg) от УВГР, м (см. рис. 12.10, в).

Из анализа дифференциальных уравнений движения частицы по относительным координатным осям x_о, y_о получаются уравнения движения частицы в параметрической форме (с независимым параметром времени t):

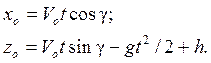(12.6)

Исключив параметр t, получим уравнение траектории относительного движения частицы:

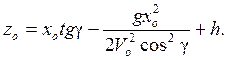(12.7)

В точке падения частицы на плоскость, лежащую на УВГР z_о = 0. Приравняв правую часть последнего уравнения к нулю и решив получившееся квадратное уравнение, получим относительную координату в точке падения, м:

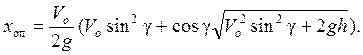(12.8)

Дальность полета частицы перпендикулярно направлению движения снегоочистителя от точки ее вылета с верхней поверхности отвала, м:

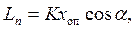(12.9)

где K – коэффициент, учитывающий влияние неучтенных факторов на дальность полета (небольшое трение снега по отвалу, боковой ветер, относящий частицы снега, расслоение слоя снега при подъеме по отвалу, его прессование или разрыхление и другие факторы). В первом приближении можно принять K = 0,7 – 0,8.

При расчетах необходимо учитывать рассеяние снега по широкой полосе вдоль пути и определять минимальное и максимальное расстояние отбрасывания снега, чтобы, при необходимости, определить параметры режима работы снегоочистителя.

12.2.2. Тяговый расчет плужного снегоочистителя

В тяговом расчете определяются сопротивления движению плужного снегоочистителя при его работе или транспортировке для выбора параметров локомотива по его тяговой характеристике. При работе, в зависимости от скорости движения машины, рабочий процесс сопровождается образованием призмы волочения и вала снега вдоль пути, или происходит отброс снега на большое расстояние от оси пути без образования призмы волочения (см. рис. 12.9). В первом случае расчетная модель аналогична модели тягового расчета струга-снегоочистителя при работе земляным устройством (см. п. 4.3). Ввиду хорошего скольжения снега по отвалу можно пренебречь составляющей, связанной с относительным движением призмы волочения и отвала, если его поверхность гладкая. В расчетах можно принимать удельное сопротивление снега резанию по табл. 12.2 [84].

Таблица 12.2

Плотность, кг/м3
Удельное сопротивление резанию, Па

При разбрасывании снега отвалом призма волочения не образуется. Поэтому сопротивление движению отвала складывается из двух составляющих: W_р – сопротивления резанию снега, Н; и W_д динамической составляющей, связанной с разгоном снега при его захвате отвалом, Н. Рассмотрим далее подход к определению динамической составляющей. Пусть снегоочиститель движется со скоростью V_v, м/с. При движении он производит расчистку траншеи высотой h_с, м и шириной B_с, м (рис. 12.11). Принимаем, что вся масса очищаемого снега получает скорость движения, равную скорости машины, соответственно, кинетическую энергию, расходуемую на подъем снега по отвалу и его отбрасывание. Работа локомотива на преодоление динамической составляющей сопротивления, Дж:

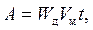(12.10)

где t – время, в течение которого совершается работа, с.

Кинетическая энергия, полученная снегом, Дж:

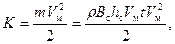(12.11)

где r – плотность снега в массиве, кг/м³.

Приравняв (12.10) и (12.11), получим выражение для оценки динамической составляющей сопротивления, Н:

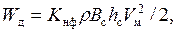(12.12)

где K_нф – поправочный коэффициент на неучтенные факторы; K_нф = 1,2 – 1,5.