Выделение областей устойчивости системы
Критерии устойчивости позволяют определить устойчива ли система регулирования, если все ее параметры - конструктивные, настроечные заданы. Однако динамические характеристики объекта регулирования и настройки регулятора в процессе эксплуатации могут изменяться в определенных пределах. В связи с этим возникает задача определения совокупности значений параметров, при которых система регулирования заданной структуры остается устойчивой.
Предположим, что в характеристическом уравнении системы регулирования
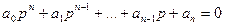 (5-17)
(5-17)
все коэффициенты, за исключением двух, например 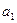 и
и 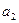 заданы. Построим плоскость с прямоугольными координатами
заданы. Построим плоскость с прямоугольными координатами 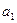 и
и 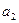 . В квадранте
. В квадранте 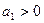 и
и 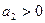 произвольно выбираем точку, для которой соответствуют коэффициенты
произвольно выбираем точку, для которой соответствуют коэффициенты 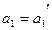 и
и 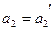 . Подставив их значения в характеристическое уравнение системы, определим корни этого уравнения. Если все найденные корни уравнения расположены слева от мнимой оси на комплексной плоскости корней, то это будет означать что система устойчива. Точку, выбранную на плоскости
. Подставив их значения в характеристическое уравнение системы, определим корни этого уравнения. Если все найденные корни уравнения расположены слева от мнимой оси на комплексной плоскости корней, то это будет означать что система устойчива. Точку, выбранную на плоскости 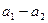 с координатами
с координатами 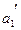 и
и 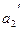 обозначим (-).
обозначим (-).
Выберем произвольно вторую точку с координатами 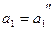 и
и 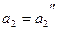 и, подставив в характеристическое уравнение значения этих коэффициентов, определим его корни. Если хотя бы один корень будет расположен справа от мнимой оси плоскости корней, то обозначим эту точку знаком (+), т.е. система регулирования при этом будет неустойчива.
и, подставив в характеристическое уравнение значения этих коэффициентов, определим его корни. Если хотя бы один корень будет расположен справа от мнимой оси плоскости корней, то обозначим эту точку знаком (+), т.е. система регулирования при этом будет неустойчива.
Если при 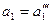 и
и 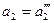 хотя бы одна пара корней лежит на мнимой оси комплексной плоскости корней, обозначим точку на плоскости коэффициентов
хотя бы одна пара корней лежит на мнимой оси комплексной плоскости корней, обозначим точку на плоскости коэффициентов 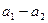 нулем, что означает границу устойчивости системы регулирования.
нулем, что означает границу устойчивости системы регулирования.
Повторяя последовательно этот процесс, дадим коэффициентам 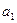 и
и 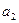 все возможные значения, отметим точки на плоскости
все возможные значения, отметим точки на плоскости 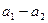 знаками (-), (+),0 и проведем кривую через точки отмеченные нулем.
знаками (-), (+),0 и проведем кривую через точки отмеченные нулем.
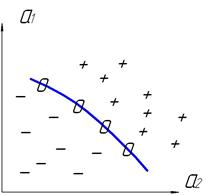
Рис. 5.6 Плоскость коэффициентов.
Эта кривая будет границей устойчивости в плоскости двух коэффициентов 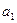 и
и 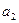 характеристического уравнения системы регулирования. (Рис. 5.6)
характеристического уравнения системы регулирования. (Рис. 5.6)
Часть плоскости, включающая совокупность точек со знаком (-) называется областью устойчивости, а часть плоскости со знаком (+) – областью неустойчивости.
Область устойчивости в плоскости двух параметров системы была впервые выделена И.А. Вышнеградским в 1877 г., профессором С-Петербургского технологического института.
Аналогично весь процесс может быть проделан для любых других коэффициентов характеристического уравнения системы, например, для трех, и в этом случае получают объем устойчивости в пространстве коэффициентов характеристического уравнения.
Работы, в которых завершена разработка приемов выделения областей устойчивости и изложена общая точка зрения на разные критерии устойчивости были выполнены в России Ю.И. Неймарком.
Выделение области или объема устойчивости называют Д-разбиением плоскости или пространства параметров системы или определением границы ее устойчивости. Границу устойчивости называют границей Д-разбиения, имея ввиду обозначения характеристического уравнения 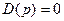 . Переход через границу Д-разбиения соответствует в плоскости корней переходу корней через мнимую ось. (Рис. 5.7)
. Переход через границу Д-разбиения соответствует в плоскости корней переходу корней через мнимую ось. (Рис. 5.7)
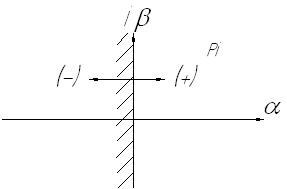
Рис. 5.7 Плоскость корней характеристического уравнения.
Отсюда следует метод определения границы Д-разбиения. Она определяется параметрически заменой в исследуемом полиноме – характеристическом уравнении 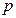 на
на 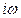 , где
, где  - переменная величина, и может быть построена при изменении
- переменная величина, и может быть построена при изменении  от -∞ до ∞. В этом смысле граница Д-разбиения есть отображение мнимой оси комплексной плоскости корней на плоскости коэффициентов характеристического уравнения.
от -∞ до ∞. В этом смысле граница Д-разбиения есть отображение мнимой оси комплексной плоскости корней на плоскости коэффициентов характеристического уравнения.
