Классификация поверхностей второго порядка

Определение. Поверхностью второго порядка называется геометрическое место точек пространства координаты которых удовлетворяют уравнению вида:

а₁₁х²+ а₂₂ у² + a₃₃z² +2а₁₂ ху + 2а₁₃ ху + 2а₂₃ уz +

+ 2а₁х + 2а₂ у +2a₃z+ c = 0, (8)

где среди коэффициентов a_ij, i,j=1,2,3 есть хотя бы один ненулевой. Выражение в первой строке называется квадратичной частью уравнения, с – свободным членом, остальное – линейная часть.

Квадратичная часть уравнения (8) представляет собой квадратичную форму. Её коэффициенты образуют матрицу

a₁₁ а₁₂ а₁₃

A = а₁₂ а₂₂ а₂₃

а₁₃ а₂₃ а₃₃

В курсе линейной алгебры доказывается, что матрицу любой квадратичной формы с помощью поворота координатных осей декартовой СК можно привести к диагональному виду

λ₁ 0 0

A¢ = 0 λ₂ 0

00λ₃

Тогда в новой декартовой СК Ox¢y¢z¢с тем же началом квадратичная часть уравнения (8) примет к вид:

λ₁x¢²+ λ₂y¢²+ λ₃z¢², (9)

который тоже называется диагональным. При этом числа λ₁, λ₂, λ₃не зависят от выбора новой декартовой СК Ox¢y¢z¢. Т.е. если ещё в одной декартовой СК квадратичная часть уравнения имеет вид (9), то набор чисел λ₁, λ₂, λ₃ будет тем же (может измениться только их порядок). Если количество отрицательных коэффициентов λ_i больше, чем количество положительных, то мы во всём уравнении поверхности поменяем знаки. Затем мы выберем именно такой порядок обозначения координатных осей, что сначала будут следовать положительные λ_i, потом отрицательные, а в конце нулевые. Таким образом, если только одно из λ_i равно нулю, то это будет именно λ₃. А если только одно λ_i ≠ 0, то можем считать что это λ₁.

Тогда набор знаков λ₁, λ₂, λ₃ будет одним из следующих: (+, +, +), (+, +, –), (+, +, 0), (+, –, 0), (+, 0, 0). Этот набор называется сигнатурой квадратичной формы. Имеем уравнение:

λ₁x¢²+λ₂y¢²+λ₃z¢² +2b₁x¢+2b₂y¢+2b₃z¢+ c = 0(10)

Далее, если все λ_i ≠ 0 мы выделим полные квадраты

λ₁(x¢² + x¢+ ) – + λ₂(y¢² + y¢+ ) – +

+ λ₃(z¢² + z¢+ ) – + c = 0,

λ₁²+ λ₂²+ ²+ c¢= 0.

Более подробно мы изучим эту процедуру выделения квадратов на практике. Затем делаем замену координат

x² = x¢+ , y² = y¢+ , z² = z¢+ ,

которая означает перенос начала координат в точку O¢(– ,– ,– ). Получим уравнение вида

λ₁(x²)²+λ₂(y²)²+λ₃(z²)² = – с'.

Затем делим уравнение на | с¢|, если с¢ ≠ 0. Тогда в правой части уравнения останется 1, –1 или 0. Мы получим одно из уравнений 1 – 6 (см.таблицу ниже).

Если λ₃= 0, то мы не можем выделить полный квадрат по z¢, но тогда преобразуем выражение 2b₃z¢+ c¢ так: 2b₃(z¢+ c¢/2b₃),и третья координата также будет участвовать в переносе начала координат в виде z² = z¢+ c¢/2b₃. В этом случае в уравнении остается слагаемое 2b₃z'', но не остается свободного члена и слагаемого, содержащего (z²)²:

λ₁(x²)²+λ₂(y²)² = –2b₃z''.

Мы разделим уравнение на | b₃| и получим одно из уравнений вида 7, 8 (см.таблицу ниже). Если при этом справа получится не 2z'', а –2z'', то это будет всё равно та же поверхность, только ориентированная по-другому относительно координатных осей.

Если λ₃= 0 и b₃= 0, то мы получим уравнение вида

λ₁(x²)² +λ₂(y²)² = – с',

которое даст нам одну из поверхностей 9 – 13 из списка.

Аналогично рассматривается и случай λ₂= λ₃= 0. Итак, мы показали, что уравнение (8) мы можем привести к одному из следующих:

Поверхность	Eё каноническое уравнение	Инварианты
1. Эллипсоид	+ + =1,	d>0 ∆<0
2. Мнимый эллипсоид (Ø)	+ + = –1,	d>0 ∆>0
3. Мнимый конус (точка)	+ + = 0,	d>0 ∆=0
4. Двуполостной гиперболоид	+ – = –1,	d<0 ∆<0
5. Однополосной гиперболоид	+ – = 1,	d<0 ∆>0
6. Конус	+ – = 0,	d<0 ∆=0
7. Эллиптический параболоид	+ = 2z,	d=0 ∆<0
8. Гиперболический параболоид	– = 2z,	d=0 ∆>0
9. Эллиптический цилиндр	+ =1,	d=∆=0 I2>0 I1∙I4<0
10. Мнимый эллиптический цилиндр	+ = –1,	d=∆=0 I2>0 I1∙I4>0
11. Пара мнимых плоскостей, пересекающихся по действительной прямой	+ = 0,	d=∆=0 I2>0 I4=0
12. Гиперболический цилиндр	– = 1,	d=∆=0 I2<0 I4≠0
13. Пара пересекающихся плоскостей	– = 0,	d=∆=0 I2 <0 I4=0
14. Параболический цилиндр	x2 = 2py	d=∆=0 I2=0 I4≠0
15. Пара параллельных плоскостей	x2 = a2	d=∆=0 I2=I4=0 I3>0
16. Пара совпадающих плоскостей	x2 = 0	d=∆=0 I2=I4=0 I3=0
17. Пара мнимых параллельных плоскостей	x2 = – a2	d=∆=0 I2=I4=0 I3<0

Здесь мы использовали инварианты:

а₁₁ а₁₂ а₁₃ a₁₁ a₁₂ a₁₃ a₁

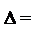d = а₁₂ а₂₂ а₂₃ a₁₂ a₂₂ a₂₃ a₂

а₁₃ а₂₃ a₃₃ a₁₃ a₂₃ a₃₃ a₃

a₁ a₂ a₃ c

I₁ = trace d =a₁₁ +a₂₂ +a₃₃

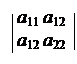
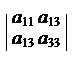
I₂ = + + – сумма диагональных мино-

ров второго порядка в d

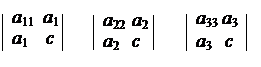– сумма диагональных мино-

I₃ = + + ров второго порядка из ∆, не

входящих в d.

a₁₁a₁₂a₁₁ a₁₁ a₁₃ a₁ a₂₂ a₂₃ a₂ – сумма диагональ-

I₄ = a₁₂ a₂₂a₂ + a₁₃ a₃₃ a₃ + a₂₃ a₃₃ a₃ ныхминоров

a₁ a₂ c a₁ a₃ c a₂ a₃ c третьего порядка

в ∆, кроме d

Теорема.Величины δ, ∆, I₁, I₂ не изменяются при любых преобразованиях декартовой СК, I₃ , I₄ не изменяются при повороте координатных осей, но меняются при переносе начала координат (без доказательства).

Поэтому эти величины называют инвариантами поверхности второго порядка. Вычислив эти инварианты мы можем определить тип поверхности, не упрощая ее уравнения. Однако так мы не сможем определить положение поверхности в пространстве и величины полуосей.

Примеры решения задач

1. С помощью переноса начала координат привести уравнение кривой второго порядка к каноническому виду. Определить тип кривой и изобразить её в исходной системе координат:

4x² + z² – 24x + 8y + 2z + 5 = 0.

Решение. Выделим в уравнении полные квадраты:

4(x² – 6x + 9) – 36 + (z² + 2z +1) - 1 + 8y + 5 = 0,

4(x – 3)² + (z + 1)² + 8y – 32 = 0,

4(x – 3)² + (z + 1)² = – 8(y – 4).

Делаем замену координат:

x¢ = x – 3,

y¢= y – 4,

z¢ = z + 1,

Она равносильна переносу начала координат в точку O'(3, 4,–1). После замены получаем уравнение

4x¢² + z¢ ² = – 8y¢, Û(x¢)² + = – 8y¢,

Это уравнение задает эллиптический параболоид, ось которого будет 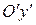. В сечении плоскостью получится эллипс + = 1 с полуосями 4 и 8. Это следует учесть при изображении.

2. Определите, какое множество определяется в декартовой системе координат неравенством

(x – 3) – 4(y + 4)² ³ 0.

Изобразите это множество.

Решение. Определим сначала, какое множество определяется уравнением (x – 3) – 4(y + 4)² = 0. Делаем замену координат

x¢ = x – 3,

y¢= y + 4,

z¢ = z .

Она равносильна переносу начала координат в точку O'(3,– 4, 0). В новой системе координат 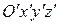получаем, что поверхность задается уравнением

(x¢ )² – 4(y¢ )² = 0. (*)

Поскольку в уравнении отсутствует координата z¢, то мы сразу делаем вывод, что наша поверхность является цилиндрической и ее образующие параллельны оси O¢z¢.На плоскости O¢x¢y¢ уравнение (*) задает пару пересекающихся прямых

(x¢ – 2y¢)(x¢ + 2y¢ ) = 0.

Эта кривая 2 порядка будет направляющей для нашей поверхности. Значит, наша поверхность – это пара пересекающихся плоскостей. Для того, чтобы не загромождать изображение мы нарисовали только небольшую часть этой поверхности. Поскольку изначально у нас было неравенство, то искомое множество – это внутренность одной из двух пар вертикальных углов, образуемых этими плоскостями. Мы возьмем любую точку на оси O¢x¢: A(a, 0, 0)_O¢x¢y¢z¢ и убедимся, что ее координаты удовлетворяют неравенству (x¢ )² – 4(y¢ )² ³ 0. Значит, ось O¢x¢ лежит в нашем множестве. Таким образом, исходное неравенство задает внутренность изображенного двугранного угла и угла, вертикального с ним. А т.к. неравенство нестрогое, то и сами плоскости тоже принадлежат множеству.

3. Составить уравнение поверхности, полученной вращением кривой

z=2y–2,

x=0.

вокруг оси a) Oz ,б) Oy . Определить тип поверхности. Изобразите ее.

Решение. Данная система уравнений задает прямую l , лежащую в плоскости Oyz. Первое из уравнений – это уравнение l в данной плоскости. Для того, чтобы составить уравнение поверхности Φ, получающейся вращением l вокруг Oz , мы должны в уравнении l оставить z без изменения, а y заменить на квадратный корень из суммы квадратов оставшихся координат: y a . Получаем уравнение

z=2 –2, Þ

x²+ y² – = 0.

Данное уравнение определяет конус, ось которого – Oz , а вершина находится в точке O¢(0, 0,–2).

Строим изображение данного конуса.

1) Подставив в уравнение конуса z = 2, получим x²+ y² = 4. Значит, в сечении плоскостью z = 2 получается окружность радиуса 2. Проводим через точку z = 2 на оси Oz вспомогательные линии, параллельно осям Ox и Oy; откладываем на них от данной точки отрезки длины 2 и через получившиеся точки проводим эллипс, изображающий окружность. При этом, масштаб по оси Ox выбираем в два раза меньше, чем по осям Oy и Oz.

2) Строим эллипс равный данному с центром в точке z = – 6 на оси Oz.

3) Проводим касательные к эллипсам через точку O¢. Подчеркнем, что точки касания ни в коем случае не совпадают с вершинами эллипса.

4) Часть нижнего эллипса, заключенную между точками касания изображаем пунктиром.

Аналогично, для того чтобы получить уравнение поверхности вращения вокруг Oy , мы в уравнении l оставляем y без изменения, а z заменяем: z a . Получаем уравнение

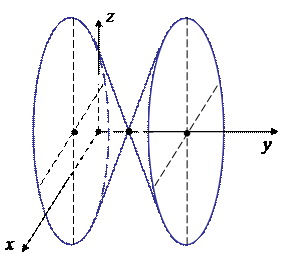x² – 4(y – 1)² +z² = 0,

– (y – 1)² + = 0.

Оно задает конус, вершина которого находится в точке O¢(0, 1, 0) , а ось конуса – Oy. Эту поверхность тоже следует изобразить. При этом, учитываем, что в сечении плоскостью y = 3 получается окружность радиуса 4.

4. Является ли поверхность заданная уравнением

– x² + + = 1

поверхностью вращения? Если да, то вращением какой кривой (написать уравнение) вокруг какой оси она получена? Изобразите ее.

Решение. Данная поверхность – это однополостной гиперболоид. В уравнении поверхности можно выделить выражение :

– x² + = 1,

и больше нигде в уравнении x и z не встречаются. Поэтому сразу делаем вывод, что это уравнение задает поверхность вращения вокруг Oy. Для того, чтобы определить, какая кривая g вращается, мы заменяем на y и получаем уравнение – x² + = 1 кривой, которая лежит в плоскости z = 0. Для того, чтобы задать эту кривую в пространстве, мы должны написать систему уравнений

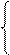– x² + = 1

z = 0

Можем заменить на z , и тогда получим уравнение кривой γ', лежащей в плоскости y = 0:

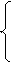– x² + = 1,

y=0.

5.Составьте уравнение поверхности, каждая точка которой равноудалена от плоскости x = – a и от точки F(a, 0, 0).

Решение. Пусть M(x, y) – произвольная точка поверхности. Тогда

| MF| = ,

а расстояние от M до плоскости равно | x + a |. По условию

= | x + a |.

Возводим это равенство в квадрат:

x²– 2ax + a² + y²+z² = x²+ 2ax + a²

y²+z² = 4ax Û + = 2ax.

Это уравнение задает эллиптический параболоид, осью которого является Ox.

6.Найдите точки пересечения эллипсоида + + = 1 и прямой = = .

Решение. Перепишем уравнение прямой в параметрическом виде:

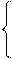x = 1 + t,

y = 4 – 6t,

z = – 6 + 12t.

Подставим эти равенства в уравнение эллипсоида:

+ + = 1,

1 + 2t + t² + 4 –12t + 9t² + 4 – 16t + 16t² = 9,

26t² – 26t = 0 Û 26t(t – 1) = 0.

Имеем два решения: t₁= 0, t₂= 1. Подставляя их в уравнение прямой, находим две точки M₁(1, 4,– 6), M₂(2, –2, 6).

Ответ: M₁(1, 4,– 6), M₂(2, –2, 6).

7. Определить, какая кривая получается в сечении поверхности + – = 1 плоскостью а)y= 2z; б)y= 2z +2.

Решение. а)Данная поверхность – это однополостной гиперболоид. Подставим y= 2z в уравнение поверхности:

+ – = 1 Û x² = 9.

Это уравнение проекции данной кривой на координатную плоскость Oxz. Оно задает пару параллельных прямых. Следовательно, наша кривая – это тоже пара параллельных прямых.

б)Подставим y = 2z +4 в уравнение поверхности:

+ – = 1 Û + = 1 Û x² = 9z.

Это уравнение проекции данной кривой на координатную плоскость Oxz. Оно задает параболу. Следовательно, наша кривая – это тоже парабола.

ПРИЛОЖЕНИЕ

Матрицы и определители.

Матрицей называется прямоугольная таблица, составленная из чисел. Матрицу принято обозначать большой буквой латинского алфавита, а её элементы – такой же маленькой буквой с двумя индексами, первый (или верхний) из которых обозначает номер строки, а второй (или нижний) – номер столбца, в которых находится данный элемент. Например,

1 2 3 4

5 6 7 8

Это матрица, состоящая из 2 строк и 4 столбцов. Говорим, что она имеет размер 2´4. В ней a₁₁= 1, a₁₂= 2, а a₂₁= 6. Матрица размера n´n называется квадратной матрицей порядка n.

Элементы квадратной матрицы, у которых номера строки и столбца совпадают, образуют главную диагональ. Если все элементы, стоящие вне диагонали, равны нулю, то матрица называется диагональной. Диагональная матрица, на главной диагонали которой стоят единицы называется единичной и обозначается буквой E. Например, единичная матрица порядка 3 имеет вид

1 0 0

E = 0 1 0

0 0 1

Если все элементы матрицы, стоящие ниже (выше) главной диагонали равны нулю, то матрица называется верхнетреугольной (нижнетреугольной).

Понятие определитель вводится только для квадратных матриц. Определитель матрицы A обозначается detA. Если вместо круглых скобок вокруг матрицы мы поставим прямые палочки, то это тоже означает определитель матрицы. Определитель матрицы порядка 2 вычисляется по формуле:

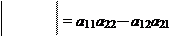a₁₁ a₁₂

a₂₁ a₂₂

Обозначим M_ij – это определитель матрицы, которая получается из матрицы A вычеркиванием i-ой строки и j-го столбца.Он называется минором, дополнительным к элементу a_ij. Тогда определитель матрицы порядка 3 можно вычислить с помощью разложения по первой строке:

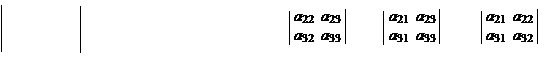a₁₁ a₁₂ a₁₃

a₂₁ a₂₂ a₂₃ = a₁₁M₁₁ – a₁₂M₁₂ + a₁₃M₁₃ = a₁₁ – a₁₂ + a₁₃ .

a₃₁ a₃₂ a₃₃

Пример.

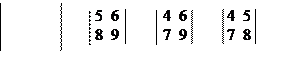1 2 3

4 5 6 =1· – 2· + 3· = 1· (5· 9 – 6 · 8) – 2· (4· 9 – 6·7) + 3· (4·8 – 5·7) =

7 8 9

= –3 +12 – 9 = 0.

Свойства определителя.

1. Если одна строка или столбец определителя состоит только из нулей, то определитель равен нулю.

2. Если определитель содержит две одинаковые или пропорциональные строки (два одинаковых или пропорциональных столбца), то он равен нулю.

3. При перестановке двух строк (столбцов) матрицы её определитель меняет знак.

4. Общий множитель элементов одной строки (столбца) выносится за знак определителя.

В предыдущем примере все элементы третьего столбца кратны трём. Поэтому мы можем вынести множитель 3 за знак определителя:

1 2 3 1 2 1

4 5 6 = 3· 4 5 2

7 8 9 7 8 3

5. Если к элементам одной строки (столбца) матрицы прибавить соответствующие элементы другой строки (столбца), домноженные на некоторое число, то определитель матрицы не изменится.

Вычтем в нашем примере из второй и третьей строки первую строку (сама первая строка при этом остается на своем месте без изменений):

1 2 3 1 2 3

4 5 6 = 3 3 3

7 8 9 6 6 6

Мы получили две пропорциональные строки, следовательно, определитель равен нулю.

6. Определитель треугольной матрицы равен произведению диагональных элементов:

1 2 –1

0 –3 6 = 1· (–3) · 9 = – 27

0 0 9

Диагональная матрица является частным случаем треугольной. Поэтому её определитель тоже равен произведению диагональных элементов.

Правило Крамера.

Пусть дана система линейных уравнений, в которой количество уравнений совпадает с количеством неизвестных. Мы ограничимся случаем, когда это число равно 3:

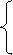a₁₁x₁ + a₁₂x₂+ a₁₃x₃ = b₁

a₂₁x₁+ a₂₂x₂ + a₂₃x₃ = b₂ (1)

a₃₁x₁ + a₃₂x₂ + a₃₃x₃ = b₃ .

Числа a_ij называются коэффициентами системы, а числа b₁, b₂, b₃ – свободными членами. Коэффициенты системы образуют матрицу A, а свободные члены – столбец B:

a₁₁ a₁₂ a₁₃ b₁

A= a₂₁ a₂₂ a₂₃ B = b₂

a₃₁ a₃₂ a₃₃ b₃ .

Обозначим D = detA, а D_i – определитель матрицы, которая получается из A заменой i-го столбца на столбец B. Например,

b₁ a₁₂ a₁₃

D₁= b₂ a₂₂ a₂₃

b₃ a₃₂ a₃₃ .

Теорема. (Правило Крамера). Если D¹0, то система линейных уравнений (1) имеет единственное решение. Его можно найти по формулам

x₁ = , x₂ = , x₃ = .

Эта теорема верна и для систем, состоящих произвольного числа n уравнений и неизвестных.

Пример. Найти решение системы уравнений

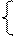5x + 9y = 3,

3x + 5y = 1.

Решение.

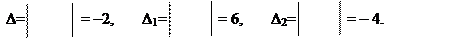5 93 9 5 3

3 5 1 5 3 1

x₁ = = = –3, x₂ = = = 2.

Ответ: (–3, 2).

Используемые сокращения

СК – система координат КС – коническое сечение

Алфавитный указатель

Асимптоты гиперболы 90

аффинная система координат

на плоскости 17

в пространстве 20

аффинный репер 16, 19

Базисные орты 18, 20

базис 16, 19

базисные векторы 15, 19

Вектор 6

вектор, отложенный из точки 7

нормали 48

нулевой 7

противоположный 8

векторная проекция 12

векторное произведение 22

вершины гиперболы 90

гиперболоида 123

конической поверхности 118

параболы 94

эллипса 87

эллипсоида 121

взаимное расположение

плоскостей в пространстве 62

прямых на плоскости 51

прямых в пространстве 62

Гипербола 89

равнобокая 91

сопряженная 92

гиперболический цилиндр 117, 132

гиперболоид однополостной 125, 132

двуполостной 125, 132

Двойное векторное произведение 28

декартова СК на плоскости 17

в пространстве 20

деление отрезка в заданном

отношении 21

диаметры КС 97

большой и малый эллипса 87

директриса 92

Инварианты кривой 2 порядка 101

поверхности 2 порядка 132

Каноническое уравнение

гиперболы 90

параболы 92

прямой 48, 64

эллипса 87

касательные к КС 94

квадратичная часть

уравнения 100, 130

коллинеарные векторы 7

компланарные векторы 7

коническая поверхность 118

коническое сечение 92

координаты вектора 16, 17, 19

точки 16, 17, 19

кривая второго порядка 100

Левая тройка векторов 12

линейная часть уравнения 100, 130

линейчатая поверхность 116

Матрица 140

матрица квадратичной части 102

метод параллельных сечений 123,

125, 128

мнимый эллипс 104

Направленный отрезок 6

направляющие косинусы 18, 21

направляющий вектор прямой 48, 63

направляющая кривая 116, 118

начало координат 17

нормальное уравнение прямой 56

Образующая 116, 118

общее уравнение кривой 2 порядка 97

поверхности 127

плоскости 60

прямой 50

оптические свойства КС 953

определитель 140

ориентируемый угол

между векторами 11

между прямыми 54

ортонормированный базис 17, 20

репер 17, 20

ось 12

Пара плоскостей 117, 121, 132

параллельных прямых 105

пересекающихся прямых 105

пара векторов левая 11

правая 11

парабола 94

параболический цилиндр 117, 132

параболоид гиперболический 128

эллиптический 128

параллель 121

параметрическое уравнение 45, 47

гиперболы 92

прямой 48, 64

эллипса 88

перенос начала координат 31

поверхность вращения 121

второго порядка 130

поворот координатных осей 32

полуоси гиперболы 90

эллипса 87

полюс 29

полярная ось 29

СК на плоскости 29

правило треугольника 7

параллелограмма 8

правая тройка векторов 12

правило Крамера 138

преобразование координат 31

общее 34

признак коллинеарности

векторов 10, 21

проекция вектора на ось

векторная 12

скалярная 12

произведение вектора на число 9

противоположно направленные

векторы 7

отрезки 6

пучок прямых 57

собственный (центральный) 58

несобственный (нецентральный) 58

Равнобокая гипербола 89

радиус-вектор 17, 19

разложение вектора по базису 17, 19

разность векторов 9

расстояние между точками 11

прямыми 68

от точки до прямой 54

репер на плоскости 16, 17

в пространстве 19, 20

Свободный член уравнения 100, 130

сигнатура квадратичной формы 131

скалярная проекция вектора 12

скалярное произведение векторов 14

скалярный квадрат вектора 14

смешанное произведение векторов 26

сонаправленные векторы 7

отрезки 6

сопряженные диаметры 98

сопряженная гипербола 90

сопряжённое направление 98

сумма векторов 7

сферическая СК 30

сферические координаты точки 30

Тор 122

тройка векторов левая 12

правая 11

Угловой коэффициент 51

угол между векторами 11

плоскостями 62

прямыми 52, 53, 67

уравнение в неявном виде 44, 46

в явном виде 45, 46

плоскости в отрезках 59

плоскости в нормальной

форме 61

прямой в нормальной

форме 54

прямой в отрезках 48

прямой в полярных

координатах 54

прямой с угловым

коэффициентом 51

Фокус 86, 89, 92

фундаментальный прямоугольник 91

Характеристическое уравнение 104

хорда КС 97

Центр кривой второго порядка 101

цилиндрическая поверхность 116

цилиндрическая СК 30

цилиндрические координаты точки 30

Эквивалентные направленные отрезки 6

эксцентриситет 93

эллипс 86

эллипсоид 123, 132

эллиптический цилиндр 117, 132

Литература

1. Погорелов А.В. Аналитическая геометрия. М.:Наука,1978

2. Погорелов А.В. Геометрия. М.: Наука, 1984.

3. Атанасян Л.С., Базылев В.Т. Геометрия. Ч.I. М.:Просвещение, 1986.

4. Базылев В.Т., Дуничев К.И. и др. Геометрия. Ч.I. М.: Просвещение, 1974

5. Атанасян Л.С. Геометрия. Ч.I. М.: Просвещение, 1973

6. Ильин В.А., Позняк Э.Г. Аналитическая геометрия. М.: Наука, 1981.

7. Постников М.M. Аналитическая геометрия. М.:Наука, 1973.

8. Постников М.M. Лекции по геометрии. Семестр I: Аналитическая геометрия. М.:Наука, 1986.

9. Александров А.Д., Нецветаев Н.Ю. Геометрия. М.: Наука, 1990.

10. Дадаян А.А., Дударенко В.А. Алгебра и геометрия. Минск: Вышэйшая школа,1989

11. Базылев В.Т. и др. Сборник задач по геометрии. М.:Просвещение, 1980.

12. Атанасян Л.С., Атанасян В.А. Сборник задач по геометрии. Ч.1. М.: Просвещение, 1973.

13. Сборник задач по алгебре и аналитической геометрии. Под ред. Феденко А.С. Минск: Изд-во Университетское, 1989, 1999.

14. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. М.: Наука, 1987

15. Александров П.С. Лекции по аналитической геометрии. М.:Наука, 1965

16. Кострикин А.И., Манин Ю.И. Линейная алгебра и геометрия. М.: Наука, 1986

17. Тышкевич Р.И., Феденко А.С. Линейная алгебра и аналитическая геометрия. Мн.: «Вышейшая школа», 1976

18. Моденов П.С. Аналитическая геометрия. М.: Изд-во МГУ, 1969