Свойства модуля комплексного числа

Обобщая сформулированные выше результаты, получаем следующие свойства модуля:

1. êzê³ 0

2. zÎR Þ êzêсовпадает с абсолютной величиной действительного числа

3. ïz₁z₂ï=ïz₁ï×ïz₂ï

4.

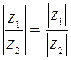
5. ïzⁿï=ïzïⁿ

6. ïz₁ï-ïz₂ï ïz₁+z₂ï ïz₁ï+ïz₂ï

Последнее свойство справедливо, поскольку служит арифметическим выражением неравенства треугольника, записанного для векторов z₁, z₂, z₁+z₂.

1.11. Извлечение корня из комплексного числа

Определение. Корнем n-й степени из комплексного числа называется такое комплексное число, n-я степень которого равна подкоренному числу: , Wⁿ=z.

Таким образом, равенство:

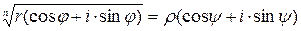
равносильно равенству

rⁿ(cos(ny)+i×sin(ny))=r(cosj+i×sinj)

Но у равных комплексных чисел модули должны быть равны, и аргументы могут отличаться лишь кратным 2p, т.е. rⁿ=r, ny=j+2pk,

откуда

где 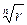есть арифметическое значение корня и k – любое целое число. Таким образом, получаем:

(*)

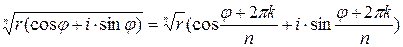т.е. для извлечения корня из комплексного числа надо извлечь корень из его модуля, а аргумент разделить на показатель корня.
В формуле (*) число k может принимать всевозможные целые значения; однако различных значений корня будет только n, и они будут соответствовать значениям:

k=0, 1, 2, ..., (n-1)

(**)

Чтобы доказать это, заметим, что правые части в формуле (*) будут различными при двух различных значениях k=k₁ и k=k₂ тогда, когда аргументы 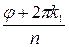и 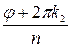отличаются не кратным 2p, и будут одинаковыми, если указанные аргументы отличаются кратным 2p. Но разность (k₁-k₂) двух чисел из ряда (**) по абсолютному значению меньше n, а потому разность 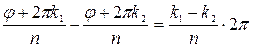не может быть кратна 2p, т.е. n значениям k из ряда (**) соответствуют n различных значений корня.

Пусть теперь k₂ – целое число (положительное или отрицательное), не заключающееся в ряде (**). Мы можем представить его в виде:

k₂=qn+k₁

где q - целое число и k₁ – любое число из ряда (**), а потому

т.е. значению k₂ соответствует то же значение корня, что и значению k₁, заключающемуся в ряде (**).

Итак, корень n-й степени из комплексного числа имеет n различных значений.

Исключение из этого правила представляет лишь частный случай, когда подкоренное число равно нулю, т.е. r=0. В этом случае все указанные выше значения корня равны нулю.

1.12. Показательная форма комплексного числа

Обобщим понятие о показательной функции на случай любого комплексного показателя. При вещественном показателе функция e^x может быть представлена в виде ряда:

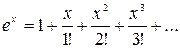
Определим аналогичным рядом показательную функцию и в случае чисто мнимого показателя, т.е. положим:

Отделяя вещественные и мнимые члены, имеем отсюда:

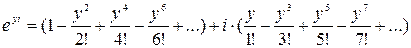
откуда, вспомнив разложения cosy и siny в ряд, определяем:

eyi=cosy+i× siny

(1)

Эта формула и определяет показательную функцию при чисто мнимом показателе. Заменяя y на (-y):

e-yi=cosy-i× siny

(2)

и решая уравнения (1) и (2) относительно cosy и siny, получим формулы Эйлера, выражающие тригонометрические функции через показательные с чисто мнимым показателем:

,

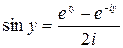(3)

Формула (1) дает новую показательную форму комплексного числа, имеющего модуль r и аргумент j:

r(cosj+i×sinj)=re^ji

Показательную функцию при любом комплексном показателе x+yi определяем формулой:

ex+yi=exeyi=ex(cosy+i×siny)

(4)

т.е. модуль числа e^x+yi будем считать равным e^x, а аргумент равным y.

Нетрудно обобщить на случай комплексных показателей правило сложения показателей при умножении. Пусть z=x+yi и w=s+ti. Тогда

e^ze^w=e^x(cosy+i×siny)×e^s(cost+i×sint)=e^x+s[cos(y+t)+i×sin(y+t)]

Но выражение, стоящее в правой части этого равенства, согласно определению (4), представляет собою:

e^{(x+s)+(y+t)×i}=e^z+w

Правило вычитания показателей при делении:

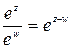
может быть непосредственно проверено путем умножения частного на делитель. В случае натурального n будем иметь:

(e^z)ⁿ=e^z×e^z×...×e^z=e^nz

Пример. Записать число в показательной форме.

Решение. Здесь

Следовательно, показательная форма числа имеет вид .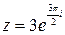

1.13. Другие арифметики для чисел а+bi

Постановка задачи. Итак, мы построили числовую систему из выражений вида a+bi, определив сложение и умножение таких выражений по формулам

(a+bi)+(c+di)=(a+c)+(b+d)I	(1)
(а+bi)(с+di)=(ас-bd)+(ad+bс)	(2)

Что касается формулы (1), то она представляется вполне естественно. Напротив, вид формулы (2) не вызывает такого ощущения. Посмотрим, нельзя ли из тех же выражений а+bi получить достаточно разумную числовую систему, сохранив правило сложения (1), но заменив (2) каким-либо новым законом умножения. Как мог бы выглядеть этот новый закон? В значительной мере это зависит от того, какими свойствами мы хотим наделить новое умножение. Скажем, было бы нелепо ввести его формулой (a+bi)(c+di)=ac²+bdi, ибо тогда, например, при b=0, d=0 мы получили бы довольно странное равенство ас=ас².

Укажем те требования, которые мы собираемся предъявить к новому умножению:

1) Умножение действительного числа а, рассматриваемого как элемент новой числовой системы (а=а+0i), на произвольное число z=b+ci должно давать тот же результат, что и в случае комплексных чисел, т. е

(а+0i)(b+ci)=ab+aci

и

(b+ci)(a+0i)=ab+aci.

В частности, это означает, что для действительных чисел новое умножение должно совпадать с обычным:

(а+0i)(b+0i)=ab+0i.

Поскольку то же самое верно и в отношении сложения (из (1) следует (a+0i)+(b+0i)=(a+b)+0i), то, тем самым действительные числа включаются в новую числовую систему с их естественной арифметикой.

2) Должно выполняться равенство

(az_l)(bz₂)=(ab)(z₁ z₂),

где а и b - любые действительные числа. Например, (2i)(3i)=6i².

3) Как для первого сомножителя, так и для второго должно выполняться свойство распределительности, связывающее умножение со сложением:

z_l(z₂+z₃)=z_lz₂+z_lz₃

и

(z_l+z₂)z₃=z_lz₃+z₂z₃.

Конечно, эти требования еще не позволяют написать до конца новый закон умножения, но все же из них следует многое. А именно,

(а+bi)(с+di)=а(с+di)+(bi)(с+di)=ас+adi+bci+bdi².

Теперь, чтобы написать результат, остается только указать, чему равно i². Приняв i²=-1, приходим к умножению комплексных чисел. Но это — отнюдь не единственная возможность. В принципе ведь нужно лишь, чтобы произведение ii принадлежало рассматриваемой нами системе чисел, т. е. было числом вида р+qi. Задав р и q, мы окончательно устанавливаем вид закона умножения:

(a+bi)(c+di)=(ac+bdp)+(ad+bc+bdq)i.

(3)

Предмет нашего изучения, таким образом, определился. Теперь можно забыть о «наводящих» соображениях, которые привели нас к формуле (3), и просто сказать, что рассматривается система чисел вида а+bi с законом сложения (1) и законом умножения (3), где р и q — два фиксированных действительных числа (определяющих собой, так сказать, «арифметику» данной системы чисел).

Внимательно рассмотрев формулу (3), мы довольно легко убеждаемся, что новое умножение обладает переместительным свойством:

z₁z₂=z₂z₁

— довольно неожиданный результат, если учесть, что среди требований, предъявленных к умножению, такого свойства не было! Выполняется и сочетательное свойство ((z₁z₂)z₃=z₁(z₂z₃)), хотя проверка этого факта требует несколько большего терпения. Имеем

[(a+bi)(c+di)](e+fi)=[(ас+bdp)+(ad+bc+bdp)i](е+fi)=((ac+bdp)e+(ad+
+bc+bdp)fp)+((ас+bdp)f+(ad+bc+bdq)e+(ad+bc+bdq)fq)i,

(a+bi)[(c+di)(e+fi)]=(a+bi)[(ce+dfp)+(cf+de+dfq)i]=(a(ce+dfp)+b(cf+
+de+dfq)p)+(a(cf+de+dfq)+b(ce+dfp)+b(cf+de+dfq)q)i.

сравнивая результаты обоих вычислений, легко убедиться в их тождественности.

Сведение к трем системам. Может показаться, что мы нашли бесчисленное множество числовых систем, поскольку в формулу (3) входят два произвольных действительных числа р и q. Но это не совсем так. Сейчас мы увидим, что любая система сводится к одной из трех:

I) числа a+bi, где i²=-1. (комплексные числа);

II) числа a+bi, где i²=1 (так называемые двойные числа);

III) числа а+bi, где i²=0 (так называемые дуальные числа).

Сведение любого, случая к одному из этих трех осуществляется следующим образом.

Из равенства i²=p+qi вытекает i²-qi=р или:

(i-q/2)2=p+q4/4

(4)

Возможны три случая:

1) p+q²/4 – отрицательное число, т.е. p+q²/4=-k², где k – некоторое отличное от нуля действительное число. Тогда (i-q/2)²=-k², т.е.

(-q/2k+(1/k)i)2=-1

(5)

Обозначив число, стоящее в скобках, через j, будем иметь j²=-1

При этом i=q/2+kj, так что любое число a+bi может быть записано в виде:

a+bi=a+b(q/2+kj)=(a+(b/2)q)+bkj;

иначе говоря, число a+bi допускает представление в виде a'+b'j, где j²=-1. Это означает, что фактически мы имеем дело с комплексными числами.

2) p+q²/4—положительное число, т, е. p+q²/4=k² (k¹0).

Тогда вместо (5) получим

Обозначив на этот раз число, стоящее в скобках, через Е, будем иметь E²=1.

Таким образом, любое число а+bi нашей системы допускает представление в виде а'+b'Е, но теперь Е²=1. Закон умножения таких чисел будет

(а'+b'Е)(с'+d'E)=(a'c'+b'd')+(а'd'+b'с')Е

Итак, при p+q²/4 > 0 получаем систему двойных чисел.

3) p+q2/4=0. В этом случае, обозначив через W число i-q/2,будем иметь W²=0.

Любое число а+bi нашей системы может быть переписано в виде
(а+(b/2)q)+bW, т, е. в виде a₁+b₁W. 3акон умножения выглядит так:

(a₁+b₁W)(c₁+d₁W)=a₁c₁+(a₁d₁+b₁c₁)W

Это система дуальных чисел.

В итоге получаем, что любая система чисел a+bi с правилами действий (1) и (3) есть одна из трех:

1) комплексные числа a+bj, j²=-1

2) двойные числа a+bE, E²=1

3) дуальные числа a+bW, W²=0.

Опыт построения системы комплексных (а также двойных и дуальных) чисел наводит на мысль пойти дальше и рассмотреть числа вида

z=a+bi+cj,

где а, b, с — произвольные действительные числа, а i и j - некоторые символы. Но из чисел вида а+bi+сj построить систему с делением невозможно. Однако оказывается, что если присоединить еще один символ k и рассмотреть числа вида

q=a+bi+cj+dk,

(6)

то можно получить систему с делением. Наиболее интересным примером такой системы являются кватернионы («четверные» числа). Так называются числа вида (6) с законом сложения

(а+bi+сj+dk)+(а'+b'i+с'j+d'k)=(a+а')+(b+b')i+(c+c')j+(d+d')k

и весьма своеобразным законом умножения. Чтобы описать этот закон, достаточно указать, чему равны всевозможные парные произведения чисел i, j, k. Положим, по определению,

i2=-1, j2=-1, k2=-1	(7)
ij=k, ji=-k, jk=i, kj=-i, ki=j,

Более подробно о кватернионах и других гиперкомплексных числах можно прочитать в книге [6].

Упражнения

1. Вычислите:

a) i⁶⁶; i¹⁴³; i²¹⁶; i¹³⁷.

b) i⁴³+i⁴⁸+i⁴⁴+i⁴⁵.

c) (i³⁶+i¹⁷)i²³.

d) (i¹³³+i¹¹⁵+i²⁰⁰+i¹⁴²)(i¹⁷+i³⁶).

e) i¹⁴⁵+i¹⁴⁷+i²⁶⁴+i³⁴⁵+i¹¹⁷.

f) (i¹³+i¹⁴+i¹⁵)i³².

g) (i⁶⁴+i¹⁷+i¹³+i⁸²)(i⁷²-i³⁴).

2. Найдите действительные значения x и y из равенств:

a) 7x+5i=1-10iy.

b) (2x+y)-i=5+(y-x)i.

c) x+(3x-y)i=2-i.

d) (1+2i)x+(3-5i)y=1-3i.

e) (2-i)x+(1+i)y=5-i.

f) (3i-1)x+(2-3i)y=2-3i.

3. Произведите сложение и вычитание комплексных чисел:

a) (3+5i)+(7-2i).

b) (6+2i)+(5+3i).

c) (-2+3i)-(7-2i).

d) (5-4i)+(6+2i).

e) (3-2i)-(5+i).

f) (4+2i)-(-3+2i).

g) (-5+2i)+(5+2i).

h) (-3-5i)+(7-2i).

4. Произведите умножение комплексных чисел:

a) (2+3i)(5-7i).

b) (6+4i)(5+2i).

c) (3-2i)(7-i).

d) (-2+3i)(3+5i).

e) (1–i)(1+i).

f) (3+2i)(1+i).

g) (6+4i)·3i.

h) (2-3i)(-5i).

5. Выполните действия:

a) (3+5i)².

b) (2-7i)².

c) (3+2i)³.

d) (3-2i)³.

e) (3+2i)(3- 2i).

f) (5+i)(5-i).

g) (a+bi)(a-bi).

6. Выполните действия:

a) ;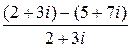

b) ;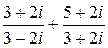

c) ;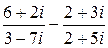

d) ;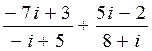

e) ;

f) ;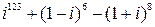

g) .

7. Решите уравнения:

a) x²–4x+13=0;

b) x²+3x+4=0;

c) 2,5x²+x+1=0;

d) 4x²–20x+26=0.

8. Изобразите на комплексной плоскости области, удовлетворяющие следующим неравенствам:

a) |z-i|<3;

b) ;

c) Rez<1;

d) .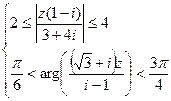

9. Запишите в тригонометрической и показательной форме комплексные числа:

a) ;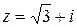

b) ;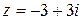

c) ;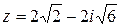

d) z=5;

e) z=-10;

f) z=6i.

10. Вычислите:

a) ;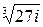

b) ;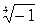

c) ;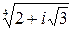

d) ;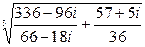

e) ;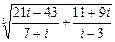

f) ;

g) ;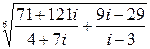

h) :

i) .